前言
由于智能手机电子屏等市场规模巨大,OLED材料和有机电子学是工业发展领域内的研究热点。本教程旨在说明如何模拟和研究OLED材料的高级电致发光现象,包括对该专题进行了一般性介绍,以及具体的研究方法。相关的研究方法主要基于下列文献:
-
P.K. Samanta, D. Kim, V. Coropceanu, J.-L. Brédas Up-Conversion Intersystem Crossing Rates in Organic Emitters for Thermally Activated Delayed Fluorescence: Impact of the Nature of Singlet vs Triplet Excited States, J. Am. Chem. Soc. 139, 4042-4051 (2017).
扩展阅读:
-
Y.Olivier, B. Yurash, L. Muccioli, G. D’Avino, O. Mikhnenko, J. C. Sancho-García, C. Adachi, T.-Q. Nguyen, D. Beljonne Nature of the singlet and triplet excitations mediating thermally activated delayed fluorescence, Phys. Rev. Materials 1, 075602 (2017)
-
Y.Olivier, J.-C. Sancho-García, L. Muccioli, G. D’Avino, D. Beljonne Computational Design of Thermally Activated Delayed Fluorescence Materials: The Challenges Ahead, J. Phys. Chem. Lett. 9, 6149-6163 (2018)
一般性介绍
OLED器件通常由掺杂有机(或金属有机)发射材料的基质材料薄膜构成。在该半导体层上施加电压产生自由电子和电子空穴,也就是所谓的电荷载流子。当电子与空穴复合时,形成强束缚的电子-空穴对,也就是所谓的“激子”。激子完全局限在单个发光分子上,因此实际上对应着该分子的电子激发态。
第一代OLED
由于自由电子、空穴自旋向上或自旋向下几率相同,因此有75%的几率形成三重激发态(电子、空穴自旋相同,导致分子总自旋S=1),25%几率形成单重激发态(电子、空穴自旋相反,导致分子总自旋S=0)。
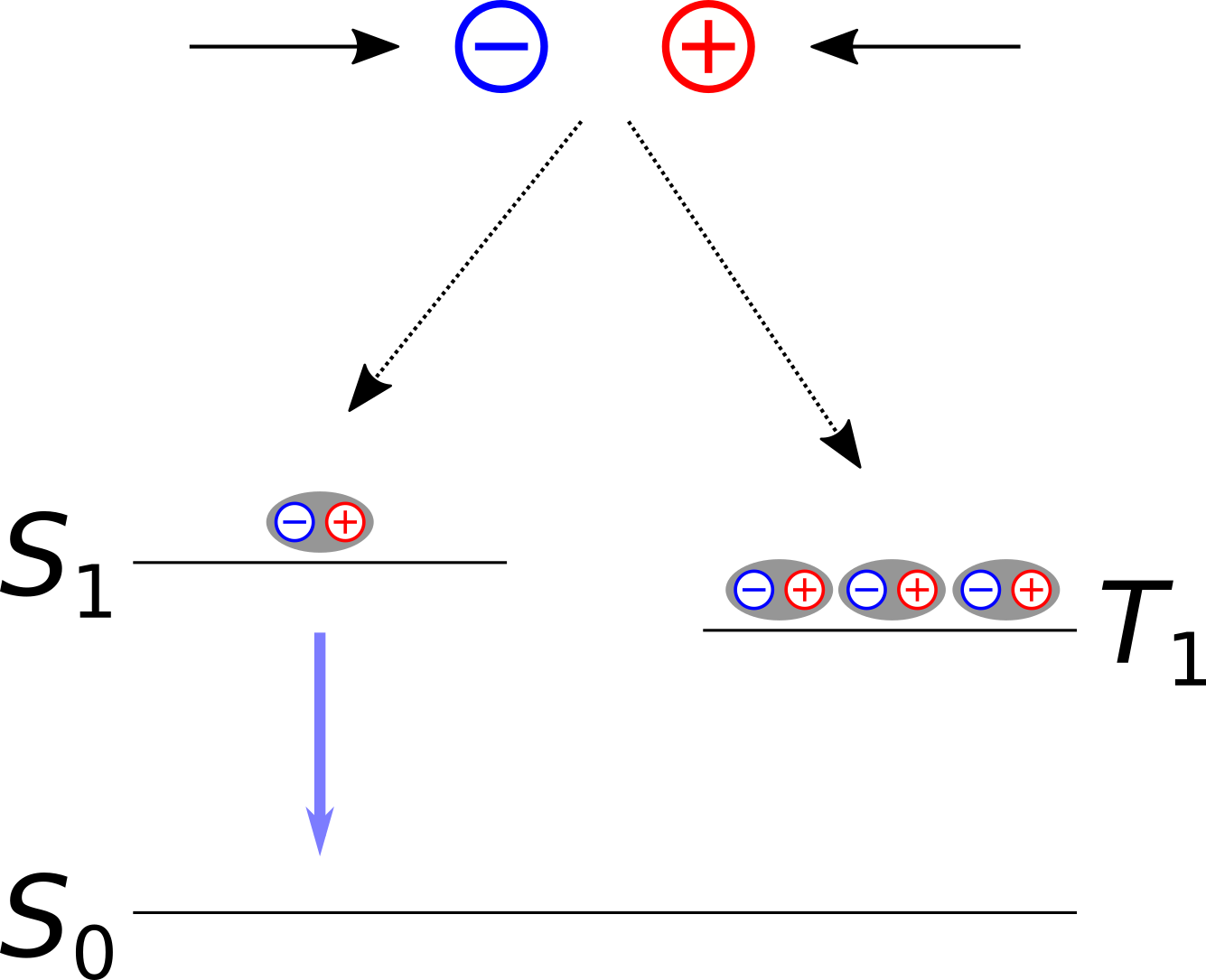
电子-空穴对通过辐射跃迁,发射出一个光子,跃迁到基态S0。这种自旋统计分布,对OLED材料的量子产率不利,因此第一代OLED发射体,存在最高25%量子产率的理论极限。如果不考虑相对论效应,从T1跃迁到S0是自旋禁阻的。如果没有自旋轨道耦合,T1到S0的发光跃迁不可能发生,荧光只能通过S1→S0跃迁产生。
第二代OLED
为了解决这个问题,出现了含重元素的染料分子的第二代OLED发光材料。这些原子(如Iridium)的价壳中的电子受到显著的自旋轨道耦合(SOC)的影响。SOC效应一方面让系间窜跃(ISC)成为可能,例如从S1→T1,从而分子处于T1态的可能性更大了,另一方面允许T1→S0跃迁,从T1→S0形成磷光发射。
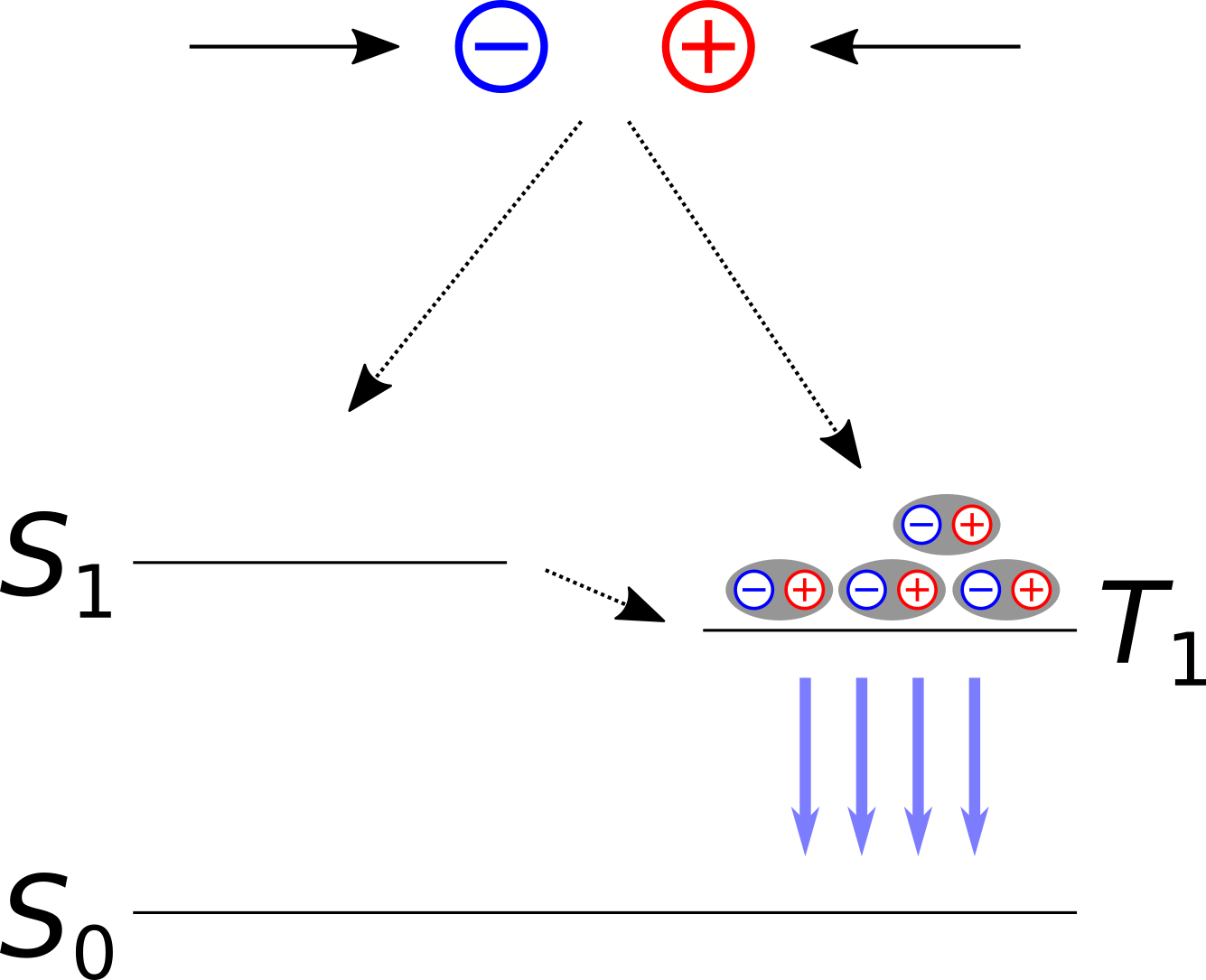
虽然这种发光机制,理论上可以达到接近100%的量子效率,但三重态寿命过长会导致化学降解,而且三重态能量与基态差越大(也即发射光的频率越高),分子越不稳定。因此,到目前为止还没有找到稳定、长寿命的深蓝光OLED材料。除此之外,这类OLED材料需要相对稀有、昂贵的重元素,大大增加了成本。
第三代OLED
这些缺点推动了第三代OLED材料的发展:某些染料分子中的S1态和T1态能量相近,并且在某种程度上存在振动耦合,就能够出现热活化延迟荧光(TADF)现象。利用TADF最大化,来规避基于SOC效应的发光材料的降解问题。此外,TADF一般出现于纯有机染料中,因此基于TADF现象的第三代OLED材料不需要昂贵的重金属元素。TADF先经历T1→S1的逆向系间窜跃(RISC)过程,然后是S1→S0的正常荧光发射过程,理论上可以达到几乎100%的量子产率:

虽然RISC与其他系间窜跃过程存在竞争,如果非辐射通道可以忽略不计,那么kRISC就可以代表TADF的效率。
逆向系间窜跃速率与量子产率
根据文献(Samanta, Bredas et al., J. Am. Chem. Soc. 139, 4042, 2017),有两个公式可以用于计算逆向系间窜跃速率(Reverse Intersystem Crossing Rate):
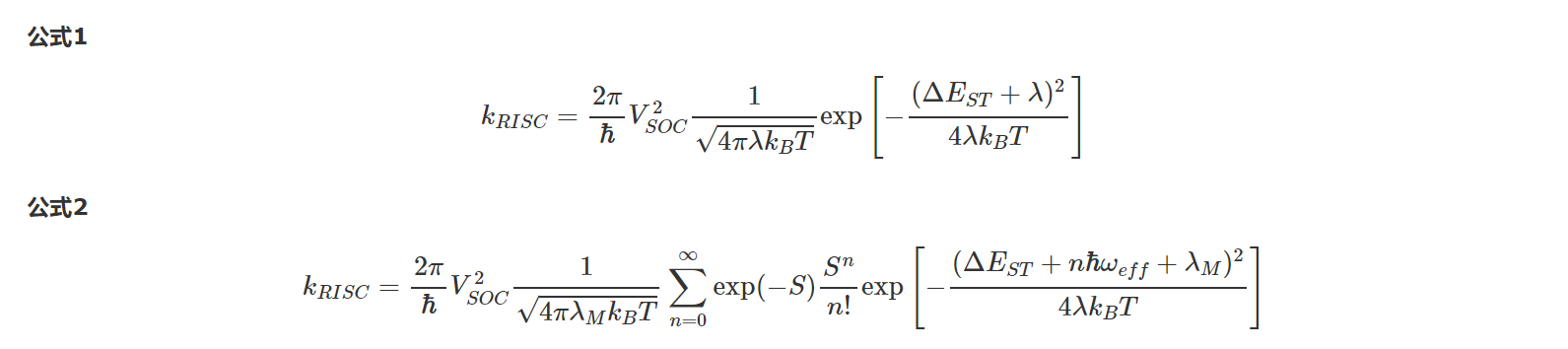
其中公式2更精确,但由于需要计算激发态频率,S1态频率计算量过大(例如一个50原子的分子,需要计算50*6=300次激发态,才能得到S1态频率),很难用于批量预测。本文通过DFTB近似计算激发态频率,最后也得到了相当好的结果,而DFTB计算激发态频率,效率就不再是问题了。当然DFTB计算激发态,也存在适用范围的问题,详见相应教程。
以下分别介绍,如何通过两种公式进行计算:
