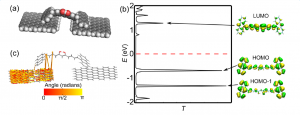
【QuantumATK亮点文章】通过一个有机分子连接的多层石墨烯电极中的连续电子输运和振动激发(ACS Nano, 2016)

Posted · Add Comment

参考文献 Burzurí, Enrique, et al. “Sequential Electron Transport and Vibrational Excitations in an Organic Molecule Coupled to Few-Layer Graphene Electrodes.” ACS Nano 10.2 (2016): 2521-2527. 在石墨烯电极中采用新的电极-分子锚定方法已经成为改进分子器件可重复性和稳定性的非常有前景的候选方案。来自荷兰Delft University of Technology等单位的研究者报道了包含单个姜黄素为基础的分子通过π-π轨道成键锚接在电极上的多层石墨烯晶体管中的连续电子输运，显示了非弹性的共隧穿激发和由于中间分子-电极耦合导致的单电子输运物理机制共存的现象，论证了中间分子的电子-声子耦合是这些振动辅助激发的起因。密度泛函理论（DFT）计算补充支持了实验的观测。DFT计算模拟了电子输运以及电子和姜黄素分子的振动方式间的相互作用，发现通过计算获得的振动方式和实验观察到的激发一致。文中分子器件的电子输运特性的计算是使用老版本的 QuantumATK软件 2014.2实现的。最新版的QuantumATK可以直接考虑电子-声子耦合，计算局域振动引起的非弹性电子输运电流。 原文链接：DOI: 10.1021/acsnano.5b07382

Read More

【QuantumATK亮点文章】III-V族半导体量子阱的能带计算方法的系统研究与实验验证

Posted · Add Comment

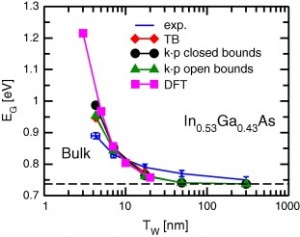
由 Synopsys QuantumWise, ETH Zürich, Università degli studi di Udine, Università degli studi di Bologna 以及IBM Zürich Research Laboratory 共同发表在 Solid-State Electronics 杂志上的文章（http://dx.doi.org/10.1016/j.sse.2015.09.005）报道了最新的关于III-V族半导体量子井的研究，评估了III-V族半导体的能带计算方法以及用于器件模拟的能带校正参数。 文章摘要 我们详细的比较了用非抛物线有效质量模型结合密度泛函理论、紧束缚方法、k·p 方法等进行能带结构计算的结果。在提取了InAs、GaAs、InGaAs等体系的用于非抛物线型Γ、L、X谷和谷间带隙参数组合之后，考察了厚度从 3 nm 到 10 nm 的量子阱以及带隙对薄膜厚度的依赖性，并与实验中In_{0.53}Ga_{0.47}As 的量子阱进行了比较。能带结构对MOSFET的源漏电流的影响则由弹道输运模型模拟。得到的结果为评估III-V族半导体能带结构计算方法和为器件计算进行能带校正参数提供了严格的依据。    Simulated and experimental energy gap for unstrained In_{0.53}Ga_{0.47}As quantum well on Al2O3. 更多关于 III-V-MOS 计划的信息: http://quantumwise.com/about-us/projects

Read More

新兴的低维电子材料研究

Posted · Add Comment

概述 自碳纳米管和石墨烯发现以来，人们开始特别关注低维材料的的特性以及可能的应用。研究者在探索相较于传统块体材料，使用低维材料实现相同功能的优越性，特别是在纳米尺度上的电子、热、化学等方面。 研究实例 低维半导体电子材料 半导体电子材料方面，常规半导体材料在摩尔定律规定下逐渐走向极限，低维材料则有结构规整、迁移率可观、栅控强等优点。在研究低维材料中，我们重点关注：（1）带隙大小的模拟以及物理和化学方法调控带隙；（2）电输运性质，主要是载流子迁移率；（3）电子材料-金属接触的电学性质；（4）构造器件的可能性以及器件性能仿真；（5）材料的稳定性。QuantumATK在以上几个方面都提供了完备的计算模拟研究工具，并在最近几年产生了大量高水准的研究成果。更多信息请参考以下专题综述文章： 二维材料构成的晶体管中的肖特基势垒 亚10纳米二维晶体管 化学与催化 在化学和催化方面，低维材料具有比结构稳定、表面积巨大等特点，特别适合负载一些催化剂活性中心，这方面的部分研究实例请参考： QuantumATK在化学与催化研究中的应用 潜在的二维光电功能器件 QuantumATK亮点文章：Janus 二维材料用于高效光电池器件（Nano Lett. 2018） QuantumATK亮点文章：二维材料光吸收和光伏效应的层数依赖关系研究 Bi2O2Se Yang, J. et al. Sub 10 nm Bilayer Bi2O2Se Transistors. Adv. Electron. Mater. 5, 1800720 (2019). Xu, L. et al. Pervasive Ohmic Contacts in Bilayer Bi2O2Se-Metal Interfaces. J. Phys. Chem. C 123, 8923–8931 (2019). 二维材料相关的初级教程 在QuantumATK中研究石墨烯 石墨烯和MoS2片层的电子输运： Transmission […]

Read More