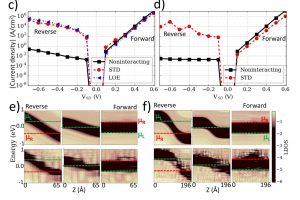
概述 晶格振动(声子)对半导体电子态,尤其是光吸收和电子输运性质有重要影响,这种影响需要在计算电子性质时考虑电子–声子相互作用(电声耦合)来体现。通常采用第一原理方法进行此类计算都非常的耗时,很难实际应用。这里介绍一种高效快速的考虑电声耦合计算非零温度电子输运性质的方法:Special Thermal Displacement(STD)方法。 STD方法的原理 这种方法由Zacharias在2016年讨论固体光吸收性质时提出【1】,其基本思想是找到一个带有“平均原子位移”(即STD)的超胞结构来代替晶格振动引起的统计效应,进而包含晶格对带隙和光吸收行为的影响,下图可以明显的看到STD随温度的变化。 STD方法有效性以及如何得到STD的理论推导详见【1】。STD 方法已经包含在QuantumATK材料与器件模拟平台中,不仅可以用于块体材料模型,也可以用于器件模型。更多关于QuantumATK的介绍,请参见文末的教程和文章列表。 应用:半导体光吸收性质 文章【1】给出了几种带隙材料的光吸收计算结果,采用这种方法计算得到的半导体材料光吸收谱与实验非常一致。 应用:器件电子输运性质 文章【2】将STD方法应用在讨论半导体器件的非弹性电子输运现象中,也取得很好的效果。下图的计算结果显示,STD方法和传统的LOE或XLOE方法(微扰方法包含完全的电声耦合对电流的贡献,详见文末的案例教程和参考文献)给出了一致的非弹性电流。下图PLDOS的计算也给出了晶格温度(300K)对能带的影响。 应用:pn结与二维器件光电流 文章【3】将这种方法与光电流计算结合,研究了硅pn结的光电流和开路电压。光电流谱结果显示,STD方法可以很好的考虑非零的晶格温度效应。 对器件在光照情况下的伏安特性研究得到了器件的IV曲线和开路电压随温度的变化关系,用STD方法包含电声耦合效应给出了更接近实验数据的结果。 文章【4】用STD方法研究了如下的二维材料(MoSSe)堆叠形成的器件的光电流特性。 STD方法的优势 由于STD方法不需要计算哈密顿量对原子坐标的导数(dH/dR),因此可以节约大量的计算时间成本。下表显示使用QuantumATK对同一体系的计算时间。很明显,STD方法由于进行了更复杂的计算,因此比不包含电声耦合的计算要慢(实际计算时还可以选择更快的收敛方法)。但是,STD方法比得到一致结果的 LOE 方法还是要快很多。更重要的是STD方法对内存的需求小很多,因此在普通的节点上即可计算,而这里的LOE方法计算则是在超大内存的胖节点上完成的。 STD方法需要对体系进行一次动力学矩阵的计算,该计算是STD最耗时的部分。为此,QuantumATK中还包含了计算动力学矩阵的Wigner-Seitz近似方法,以避免使用耗时的有限位移超胞方法,可以大大加快动力学矩阵的计算速度。 案例教程 QuantumATK中包含了LOE、XLOE 和 STD等考虑电声耦合计算非弹性电流的方法以及光电流计算工具等: LOE/XLOE:https://docs.quantumwise.com/tutorials/inelastic_current_in_si_pn_junction/inelastic_current_in_si_pn_junction.html STD方法:https://docs.quantumwise.com/casestudies/std_transport/std_transport.html 光电流计算:https://docs.quantumwise.com/tutorials/photocurrent/photocurrent.html 参考文献 【1】STD方法原理与光吸收计算:Marios Zacharias and Feliciano Giustino. One-shot calculation of temperature-dependent optical spectra and phonon-induced […]
QuantumATK独有的新功能:考虑电声耦合效应的用于更有效和准确的模拟真实的整流器和晶体管新方法
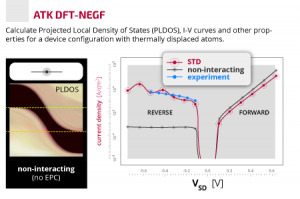
Synopsys QuantumWise公司与丹麦科技大学的研究组开发了一种处理电声耦合(EPC)效应的用低成本进行大尺度计算的方法,称为“特殊热位移(STD)-Landauer方法”[1]。EPC效应(例如声子辅助隧穿)在大尺度电子器件性能中起到核心作用,并且无论从实验和模拟角度考虑都是这一领域的主要挑战之一。STD-Landauer方法概念非常简单(见下文图片)并且在第一性原理方法模拟真实的整流器和晶体管方面比任何已有的考虑EPC效应的第一性原理输运方法都更高效。 概念 与实验结果比较 在文献[1]中,考虑了EPC效应后计算得到的二维硅n-i-n双栅场效应管和硅p-n结的伏安特性(I-V)曲线计算中和硅纳米线和块体的载流子迁移率,都与实验结果和最先进微扰理论计算结果高度吻合。因此,STD-Landauer方法将成为对下一代器件和纳米材料进行原子尺度设计的有力工具。 相关资源 案例研究:请参考根据文献[1]准备的案例研究学习如何使用STD-Landauer方法计算硅p-n节器件伏安特性曲线和投影局域态密度(PLDOS)。您可以使用VNL用户界面进行二维硅n-i-n双栅场效应管,硅p-n结和硅纳米线以及块体的建模。STD-Landauer方法和另外一种考虑电声耦合效应的计算方法MD-Landauer [3] 已经由Synopsys QuantumWise公司在International Workshop on Computational Nanotechnology研讨会上发布(幻灯片下载) 参考文献 [1] T. Gunst, T. Markussen, M. L. N. Palsgaard, K. Stokbro and M. Brandbyge, “First principles electron transport with phonon coupling: Large scale at low cost”, Phys. Rev. B 96, 161404 (R) (2017). arXiv, pages 1706.09290, 2017. URL: arXiv:1706.09290. […]
QuantumATK独有的新功能:考虑电声耦合效应能够准确和高效的计算电阻率和迁移率的新方法
Synopsys QuantumWise公司与丹麦科技大学的研究组使用QuantumATK软件发表了一篇Phys. Rev. B文章[1]。文章介绍了一种 MD-Landauer 的新方法,将格林函数输运计算和分子动力学模拟结合,准确、高效的考虑 电声耦合(EPC)效应 的影响下的电阻率和迁移率。电声耦合效应在大部分电子器件中扮演着至关重要的作用。在各种体系(如硅和金纳米线,硅和金块体,碳纳米管和石墨烯,见图表1)中,MD-Landauer方法都得到了实验结果和使用目前流行的玻尔兹曼输运方程(BTE)方法计算的验证[2]。迁移率和电阻率的计算半定量的与BTE方法计算和实验结果一致,变化趋势完全重现。这表明 MD-Landauer 方法在考虑大体系和复杂体系(如非晶,缺陷和替位)的电声耦合效应中可以代替BTE方法。全尺度密度泛函电声耦合计算已成为可实现的方法,并且MD-Landauer方法在计算时间上更为合理。 Fig.1.MD-Landauer方法的图解: 1. 体系在Maxwell-Boltzmann分布的随机初始速度和目标温度下用分子动力学平衡一系列(10-50)MD轨迹,得到该温度下的一组结构;2. 使用ATK-DFT-NEGF方法对所有得到的结构进行电子透射计算,并将透射函数进行平均得到目标温度下的透射;3. 温度相关的电阻率由得到;4. 进一步由电阻率和态密度可以得到迁移率。 相关资源 Synopsys QuantumWise公司根据此文制作了金块体电阻率计算的案例。在网站上您可以找到关于 计算透射/电阻率 和 评估迁移率(使用BTE方法)的教程。其中所涉及的如硅和金纳米线和块体,碳纳米管和石墨烯都可以使用VNL图形用户界面进行建模和结构优化。 QuantumATK在处理电声耦合效应方面更高效的方法文章也已经发表,主要介绍特殊热位移(STD)-Landauer方法(STD-Landauer)以及其在超大尺度硅器件中的应用[3]。 MD-Landauer和STD-Landauer两种方法都已经由Synopsys QuantumWise公司在International Workshop on Computational Nanotechnology会议上发布。 参考文献 [1] T. Markussen, M. Palsgaard, D. Stradi, T. Gunst, M. Brandbyge and K. Stokbro, “Electron-phonon scattering from Green’s function transport combined with molecular dynamics: Applications to mobility […]
免费在线讨论会:特殊热位移(STD)-Landauer方法模拟大尺度原子器件电-声散射效应
欢迎参加“特殊热位移(STD)-Landauer方法模拟大尺度原子器件电-声散射效应”免费在线研讨会。电-声散射效应在纳米尺度电子器件,例如整流器、晶体管中,具有重要影响。 时间:2017年12月14日 16:00~16:30(北京时间), 2017年12月15日 03:00~03:30(北京时间) 两场内容相同,请任选一个时间参加。 报告人:来自Synopsys QuantumWise公司的Daniele Stradi, PhD和Ulrik Grønbjerg Vej-Hansen, PhD 本次研讨会面向: – 从事原子级器件模拟的ATK用户 – 从事TCAD器件模拟的工程师/研发人员 本次研讨会内容: – 为什么电-声散射效应在纳米电子器件中起到核心作用? – STD-Landauer方法是如何考虑电流中明显包含的电-声耦合的?为何这种方法特别的高效? – 通过硅p-n结案例(https://docs.quantumwise.com/casestudies/std_transport/std_transport.html),学习如何设置、运行STD-Landauer计算,分析结果; – STD-Landauer方法在计算半导体器件电性质方面的应用案例; – 问题与讨论 注册报名 注册后,您将受到一封确认邮件,包含参加在线研讨会的信息。关于本次在线研讨会的任何问题,请联系info@quantumwise.com 关于STD-Landauer方法,您可以点击这里了解更多:http://bit.ly/2i8wS94
VNL-ATK 2017新版发布
QuantumWise已于7月1日正式发布了VNL-ATK 2017版,新版引入了多种新的计算方法和大量的性能优化。 更新概要 大幅改进电声耦合计算性能 新的“special thermal displacement”近似方法,高效描述声子辅助隧穿 新增两种计算精确带隙的方法 改进默认参数设置 创新性的Wigner-Seitz方法加速大超胞的动态矩阵计算 输出文件改为HDF5格式 新增多种酷炫的2D、3D作图选项 变晶胞NEB过渡态搜索(模拟相变) 连接Materials Projects和COD数据库(或自建数据库) 完整的投影能带和DOS License信息 已经获得2017之后版本授权的用户,直接下载安装即可使用; 最后版本为2016与之前的版本的用户,欢迎联系我们(sales@fermitech.com.cn)付费升级事宜; 欢迎各位新老用户联系我们(sales@fermitech.com.cn)获取最新版的试用许可。 本次更新详情 电声耦合计算 显著降低内存消耗(稀疏矩阵存储) 典型测试显示内存需求从800GB降为1.3GB 计算迁移率的新方法:常数弛豫时间方法(与BoltzTraP代码类似) 弛豫时间可以由实验确定,也可以从动态矩阵计算并在能量/k点取平均 对于电极材料重复形成的器件(长的纳米线、纳米管、二维片层)体系,非弹性电流计算速度提高100000倍,因为仅计算电极的动态矩阵和哈密顿量导数 将所有声子模式在能量范围内分组求和(近似),提速10-100倍 突破性进展 ATK2017引入了一种全新的特殊热位移(special thermal displacement;STD)近似,来考虑声子散射对IV曲线的影响。 STD-Landauer方法详见(PRB文章已发表),这种方法将全电子-声子耦合计算减少为中间区域的动态矩阵(LOE/XLOE计算所必须的)和每个偏压(温度)下的一个器件计算。基本思想是根据全部声子的正则系综平均生成单个的原子位移组合,即可包含所有的温度效应。 文章演示了这种方法是如何高效的研究声子对硅p-n结电流、硅块体和纳米线的迁移率的影响随温度变化的效应(图)。 总体性能改进 费米面以上能带数现自动设置 提速约2倍;过去版本可以手动设置,但多数用户都未注意到这个选项 新的自能存储选项 NoStorage(大大减少大体系的内存占用,但是每次重新计算) SaveInMemory(快速,但耗内存) StoreOnDisk(快速,不消耗内存,但消耗硬盘空间) 中间区域不同,但是电极相同时,重复使用自能计算结果 SparseGreenFunction改进 使用可以减少大洁面体系的内存消耗 尤其对于有限偏压时,每个能量(k)点使用多进程可以大大减少每个MPI进程的内存 No performance overhead anymore for the distributed Pulay mixer […]
【QuantumATK亮点文章】第一原理方法计算电子-声子耦合和电子迁移率
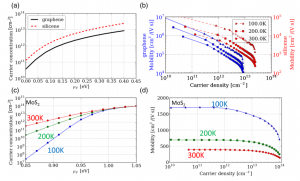
Synopsys QuantumWise和DTU Nanotech联合发表了题为“第一原理方法计算电子-声子耦合和电子迁移率:在二维材料中的应用”的文章(Phys. Rev. B 93, 035414 (2016))。 文章摘要 “我们采用密度泛函理论计算了n-型单层石墨烯、硅烯和MoS2的声子限制的电子迁移率。包括电子-声子耦合在内的材料的性质都采用第一原理完成。我们详细叙述了归一化的全能带弛豫时间近似与线性的玻尔兹曼方程(BTE)的方法来描述非弹性散射过程。块体电子-声子耦合采用超胞方法计算。这是一种完全的数值方法,因此不需要任何解析方法来处理问题,尤其是可以保留电声耦合和能带的各向异性信息。进一步计算可以得到低场的迁移率及其对载流子浓度和温度的依赖关系,加深对石墨烯、硅烯和单层MoS2材料的电子输运性质的理解。与石墨烯不同,硅烯中的载流子与面外振动模式相互作用很强。我们发现在硅烯面外振动模式的影响被限制接近于零(由于基底的影响,原子固定等类似情况)的情况下,石墨烯中的迁移率比硅烯仍然高出不止一个数量级。而当硅烯的面外振动模式没有限制时,硅烯中的迁移率基本为零。对于MoS2,我们得到的迁移率数值比石墨烯中低几个数量级,这与最近的其他理论计算吻合。模拟结果表明了新实现的基于第一原理和局域基组的BTE方法和模拟可以很好的预测材料的输运性质。” 相关实例教程 迁移率: 使用QuantumATK可以方便的研究: 由DFT方法计算电子布洛赫态和能量、声子模式和能量以及电子-声子耦合等信息使用玻尔兹曼输运方程计算电子迁移率 计算声子态、分析畸变势、电声耦合(右图),并在此基础上计算温度对迁移率的影响 使用大规模MPI并行可以大大减少计算时间 教程链接 更多QuantumATK在半导体材料研究的应用详见【这里】。