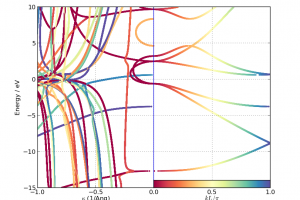
复数能带的概念和求解方法 对于周期性固体,薛定谔方程 Hψnk=EnkSψnk (S为重叠矩阵)中的 ψnk 可以写为 ψnk(r)=e−ik⋅rUnk(r),这里的 Unk(r) 是与晶体自身周期性相同的周期函数。在一般的能带结构计算中,给定一系列实数的波矢k(通常位于第一布里渊区的高对称方向上) ,可以通过求解上面的薛定谔方程得到不同 k 值上的本征矢,由此确定本征能量 Enk (即能带结构)。 在给定能量 E时,可以求解满足薛定谔方程的 k 值。这种解法可以得到实数和复数的 k,实数 k 的解是通常的 Bloch 态,而带有虚部的解是在一个方向上呈指数递减,相反方向上递增。这样的解通常不能稳定存在于块体材料中,因此在能带结构计算中通常被忽略。然而,它们可以存在于表面或界面处,并且可以提供关于电子态如何在材料中衰减的信息。计算复数能带的方法可参考: Yia-Chung Chang and J. N. Schulman. Complex band structures of crystalline solids: An eigenvalue method. Phys. Rev. B, 25:3975–3986, Mar 1982. doi:10.1103/PhysRevB.25.3975。 复数能带与衰减电子态 下图清楚的显示了复数能带上不同点的波函数形态:实数能带具有完整的周期性,而复数能带则呈现衰减态。 复数能带与电子透射 对于导电结,很自然地可以通过材料的电导-长度依赖性β来表征材料,此依赖性可以通过计算复数能带获得。更多关于复数能带结构的概念和在导电结中的应用,请参考: Jensen, A. et al. Complex band structure […]
近期活动日历
周日周一周二周三周四周五周六日一二三四五六3031123456789101112131415161718192021222324252627282930123近期活动列表
- 没有活动
- 所有活动
标签
关于费米科技
费米科技以促进工业级模拟与仿真的应用为宗旨,致力于推广基于原子级别模拟技术和基于图像模型的仿真技术,为学术和工业研究机构提供研发咨询、软件部署、技术攻关等全方位的服务。费米科技提供的模拟方案具有面向应用、模型新颖、功能丰富、计算高效、简单易用的特点,已经服务于众多的学术和工业用户。
-
最近更新
- 水滑石/硼酸锌/改性环氧树脂复合阻燃涂层的制备及其阻燃性能 2025年4月25日
- Co-TMDC 磁性隧道结:自旋电子学的新前沿 2025年4月18日
- 锂电池电极建模:基于 CT vs DFN 模型 2025年4月14日
- 【辽宁工程技术大学】褐煤在ReaxFF MD高温条件下的燃烧机理分析(Fuel 2025) 2025年4月12日
联系方式
- 留言板:点击留言
- 邮箱:sales_at_fermitech.com.cn
- 电话:010-80393990
- QQ: 1732167264
订阅费米科技新闻
- 邮件订阅:
您可以使用常用的邮件地址接收费米科技定期发送的产品更新和新闻。
点击这里马上订阅! - 微信订阅:
微信扫描右侧二维码。
- 邮件订阅: