通过基于 Micro-CT 重建的孔隙尺度模型和数值模拟研究泡沫混凝土的渗透特性

概述

泡沫混凝土主要由水泥浆和使用配制泡沫或专业化学发泡剂产生的较大体积气孔组成，较高的流动性、隔热性、能量吸收以及承受大变形的能力使其在土木工程中越来越受到关注。在大多数的应用中，泡沫混凝土的耐久性是一个不可避免的问题，而渗透性是决定长期耐用性的重要材料特性之一。

本项目提出了一种结合基于 X 射线显微计算机断层扫描（Micro-CT）图像重建技术和 Simpleware 软件研究泡沫混凝土渗透特性的方法。通过 3D 孔隙尺度结构模型讨论影响泡沫混凝土渗透性的主要因素，进一步分析边界条件对渗透率计算结果的影响。

试样制备

泡沫混凝土由 #42.5 普通硅酸盐水泥（OPC）、商业复合发泡剂和自来水组成。设计不同的目标湿密度，水/水泥（w/c）比率恒定为 0.45。圆柱体试样高 70mm，直径为 50mm。

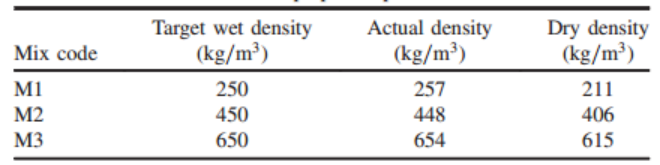
采用高性能 Micro-CT 扫描设备（Zeiss Xradia 410Versa, Pleasanton, California）对所有试样进行扫描，然后将图像数据导入 Simpleware ScanIP 进行图像处理。

图2：不同密度泡沫混凝土的 2D 切片视图和 3D 重建模型（a）M1（b）M2（c）M3

计算模拟

一般情况下，当模型尺寸比孔隙大 10 倍时，可以忽略尺寸的影响。泡沫混凝土中大部分孔隙的直径小于 1.5 mm。因此，为节省计算时间和资源，裁剪 15×15×15 mm 的立方体模型进行研究。同时考虑到模拟结果的可靠性，选取了三个不同位置的计算模型。

在 Simpleware FE 模块为计算模型生成高质量的四面体网格模型，网格粗糙度设置为 0，沿 Z 方向定义流体的入口压力 20 Pa和出口为开放边界。假设流体仅通过孔隙且不渗透水泥基体，设置侧壁为不渗透边界。在流固界面上施加无滑移条件，假设流体为水。在 Simpleware FLOW 模块进行渗透模拟，计算渗透率。

结果与分析

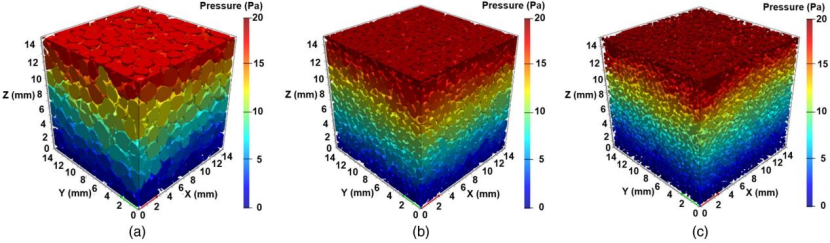
泡沫混凝土中的压力和水流分布

水的压力如预期地从上到下逐渐减小，由于孔隙分布的不均匀性，z 平面上的压力也分布不均匀。选择 x = 7.5 mm 处截面展示泡沫混凝土中水的速度分布和流线，M3 的最大速率是三种试样中最小的（11 mm/s），相较下 M1（93 mm/s） 和 M2（34 mm/s）分别增长了 845% 和 309%。

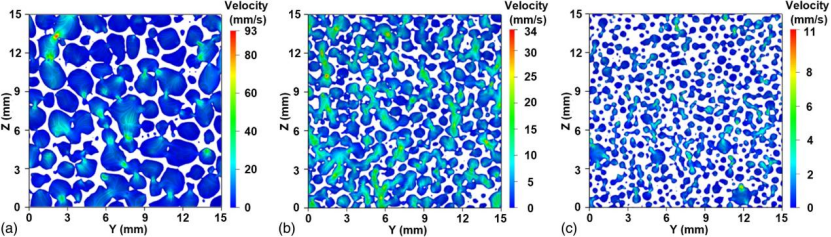
不同密度泡沫混凝土的渗透率

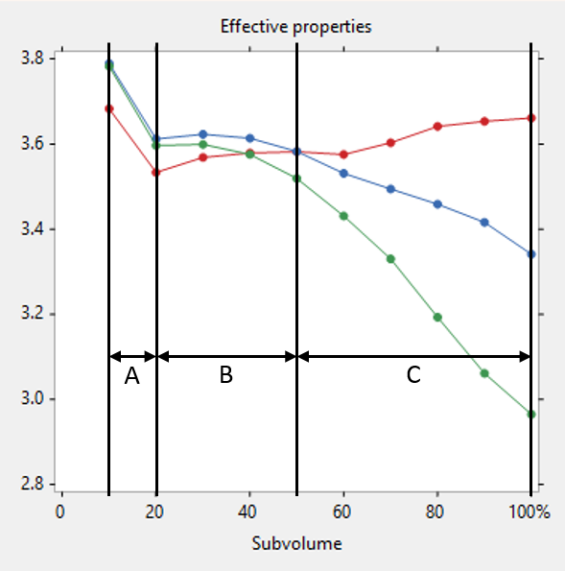
从每个密度的泡沫混凝土中选取 3 个尺寸为 15 × 15 × 15 mm 的计算模型。为避免边界效应的影响并验证所选感兴趣区域是否足够大到具有代表性，为每个计算模型创建从 10％ 到 100％ 的10个不同子体积模型。

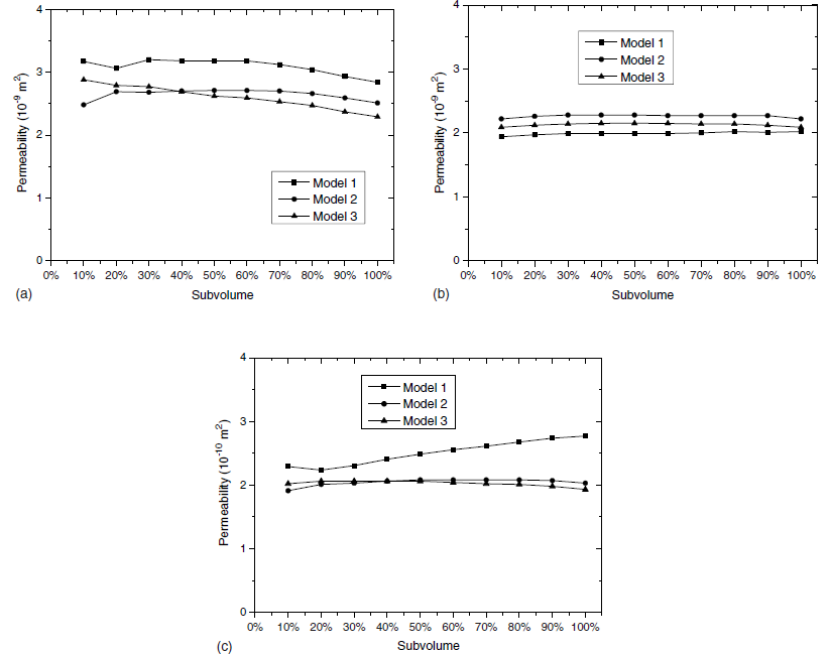
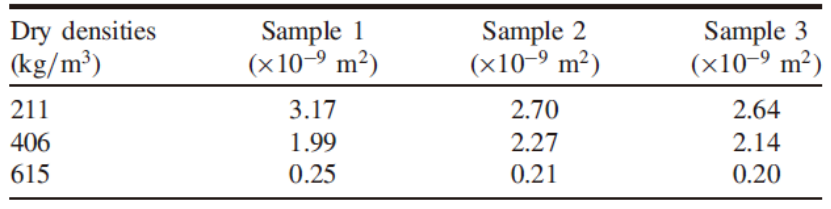
在 Simpleware 教程案例中，区域 A 代表的子体积太小而无法准确代表整个样本，区域 B 是代表最准确数值的稳定区域，区域 C 受到边界存在的强烈影响。本研究仅采用区域 B 的计算结果，泡沫混凝土的渗透率随着密度的增加而降低，M1、M2、M3的平均渗透率分别为 2.84×10⁻⁹ m²、2.13×10⁻⁹ m²、0.22×10⁻⁹ m²。

讨论

影响泡沫混凝土渗透性的主要因素

泡沫混凝土的渗透性能与孔隙结构、内表面积、毛细管压力梯度等基本物理性能有关，并且还受到多种因素如 w/c、水化程度、养护温度、矿物掺合料的使用和添加聚合物的影响。泡沫混凝土的渗透率随密度不同发生剧烈变化，从 M1 到 M2 渗透率下降 25%，而从 M2 到 M3 渗透率仅为原来的十分之一。

设置固体密度为 1870 kg/m³，利用公式计算得到 M1、M2、M3 的孔隙率分别为 0.89、0.78、0.67。通过幂律模型揭示泡沫混凝土的孔隙率与渗透率之间的关系，获得散点图及其拟合曲线。

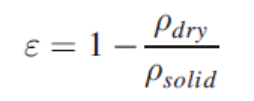
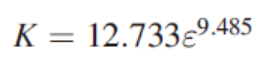
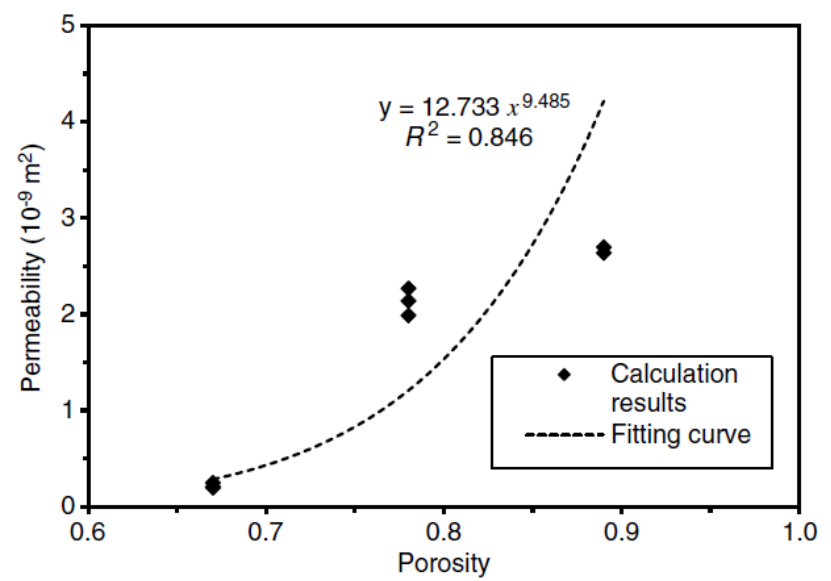
为进一步揭示渗透率的影响因素，采用基于最小二乘非均匀样条方法，根据不同类型的颗粒连通性标记不同密度下泡沫混凝土的连通区域。随着密度增大，孔隙的连通性和均匀性也逐渐增加，可以推断渗透率计算结果的离散性应该随着密度的增大而减小。

边界条件对渗透率计算结果的影响

边界条件也是数值模拟中影响渗透率结果的因素。在 Simpleware 软件中，除提供“不渗透侧壁”边界条件外，还有在侧壁上施加“线性压力变化（弱施加）”的边界条件。当计算模型较小时，其结果比较稳定，与“不渗透侧壁”边界条件的结果一致。随着模型增大，计算结果的偏差越来越大，其稳定性不如“不渗透侧壁”边界条件。这种情况可以解释为，在大的计算模型中包含大孔径的概率也相应增加，不均匀性变得更加明显，可能导致线性压力条件与实际情况偏差更大。

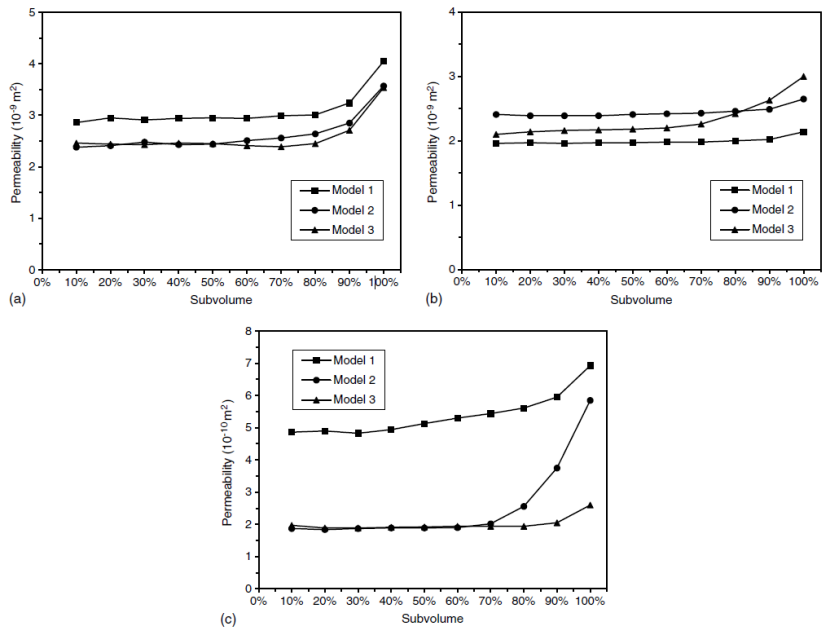
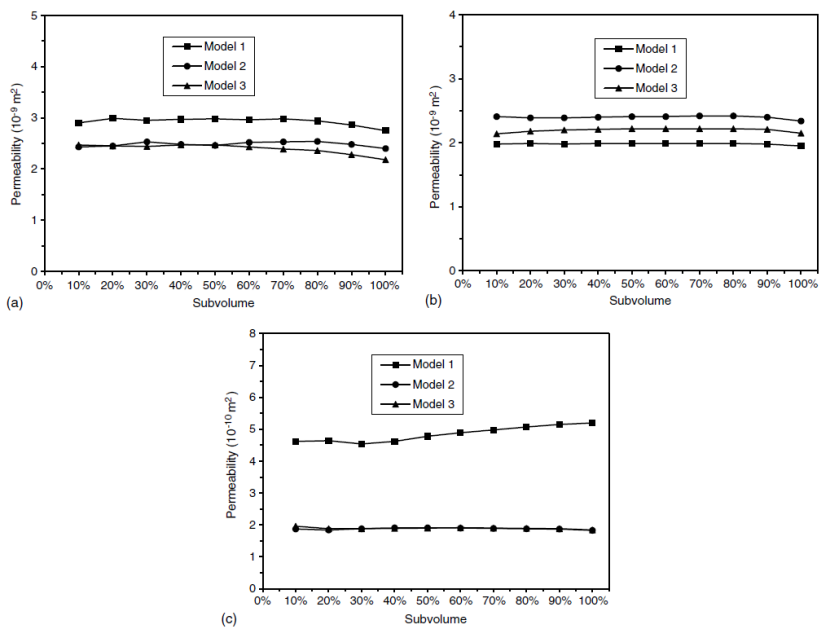
2D 和 3D 结果比较

通过 2D 模型计算的泡沫混凝土渗透率与 3D 模型结果基本相同，因为泡沫混凝土通常被认为是各向同性。由于 2D 模型很容易受到不均匀大孔隙的影响，其计算结果的离散度要比 3D 模型的大。因此，还是很有必要将 2D CT 图像重建为 3D 孔隙尺度物理模型研究泡沫混凝土的渗透率。

结论

在本研究中，对湿密度分别为 250、450 和 650 kg/m³ 的三组圆柱形泡沫混凝土试样进行研究。采用 Micro-CT 技术获得微观结构，使用 Simpleware 软件将 2D CT 图像重建为 3D 孔隙尺度物理模型并进行计算模拟，获得压力和水流分布及渗透率。

1. 利用建立的幂律模型揭示孔隙率与渗透率之间的关系，泡沫混凝土的渗透率随着孔隙率的增大而升高。
2. 随着模型增大，计算结果的偏差越来越大，“线性压力变化（弱施加）”边界条件的稳定性不如“不渗透侧壁”边界条件。
3. 通过 2D 模型计算的泡沫混凝土渗透率与 3D 模型结果基本相同，但 2D 模型很容易受到不均匀大孔隙的影响，其计算结果的离散度更大。

参考

• Yuan J, Chen W, Tan X, et al. Study on the permeability characteristics of foamed concrete using a pore-scale model from X-ray microcomputed tomography image reconstruction and numerical simulation[J]. Journal of Materials in Civil Engineering, 2021, 33(6): 04021117.