概述
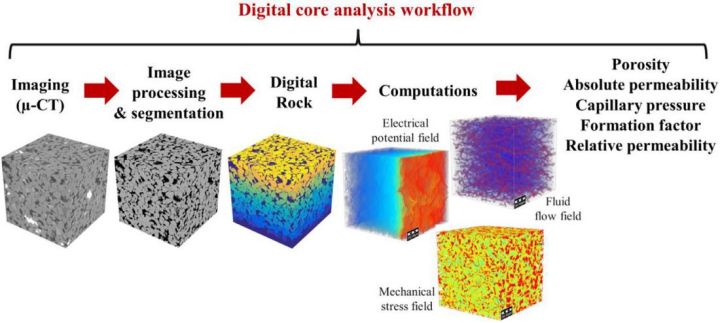
数字岩石物理(DRP)是一种快速发展的多学科工具,可用于计算岩石性质(如孔隙率、渗透率、地层因子、I-Sw 曲线、毛细管压力曲线和相对渗透率),并采用高分辨率图像(如 x 射线计算机断层扫描、扫描电子显微镜)表征微观结构。
在某些情况下,DRP 可以起到补充作用,取代实验室中相对缓慢且昂贵的测量和根据经验趋势获得模型的需求。此外,将岩心柱上的 DRP 工作流程与同一柱体上的物理测量相结合,可以在更大长度范围内实现更可靠、更详尽的地层评估和表征。本研究对包含理想化和异质化的不同微观结构进行图像处理,利用多种不同数值模拟方式计算渗透率并对结果进行比较。
亮点
- 采用 36 个包含理想化和异质化的微观结构
- 使用 12 种不同的数值模拟方式计算渗透率
- 对于比较各种数值模拟的速度和精度具有重要参考意义
理想化微观结构和数字岩石
在这项研究中,使用 36 个微观组织生成绝对(单相)不可压缩渗透率的数值参考,其中包含一组具有不同横截面形状、直径(固定值及其正弦变化)的管道结构,5个 2D 岩石结构,1 个球体填充结构和 5 个由 micro-CT 扫描获得的数字化 3D 岩石结构。这些结构的孔隙空间复杂程度不等,除球体填充 Sp.pa. 外,其余结构均为 10243 体素。选择这些样本是因为它们涵盖了可能遇到的组合和纹理的范围。
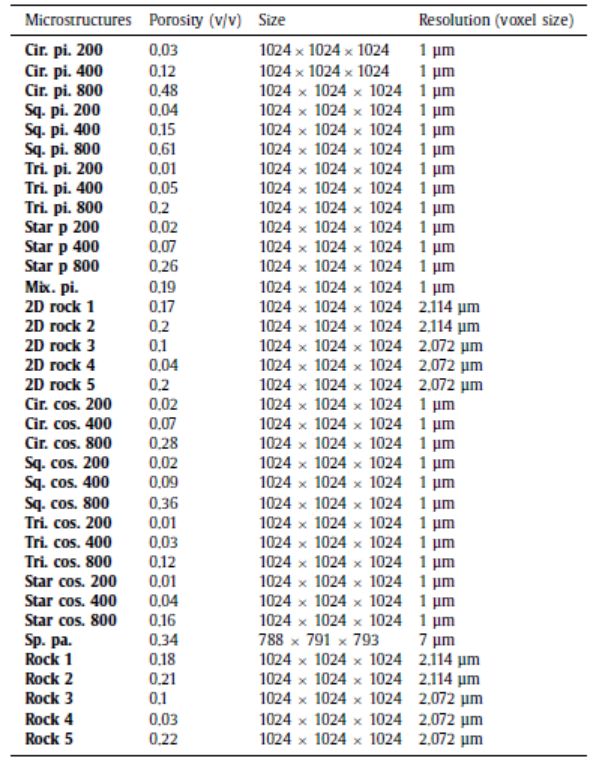
- 2D 管道:12 个结构内有一个与流动方向垂直的相同截面管道,截面形状分别为不同尺寸的圆、正方形、三角形、六角形;
- 2D 正弦管道:12 个由以上形状沿流动方向呈正弦变化的三维结构;
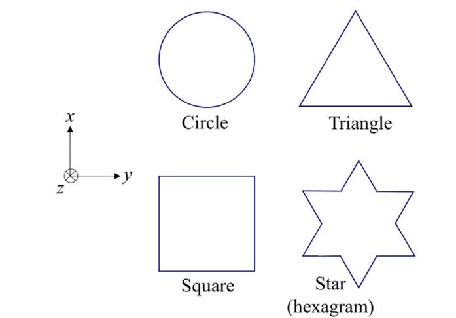
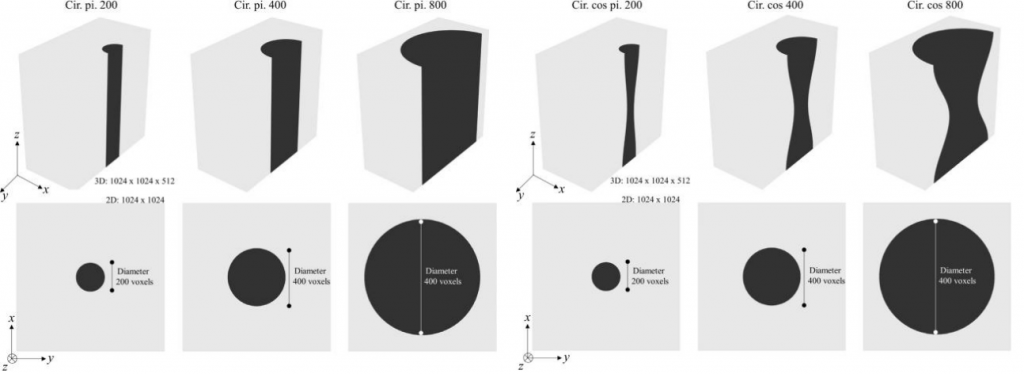
- 2D 混合:1 个结构内有一个与流动方向垂直的相同截面,截面为 4 个直径不同的圆形;
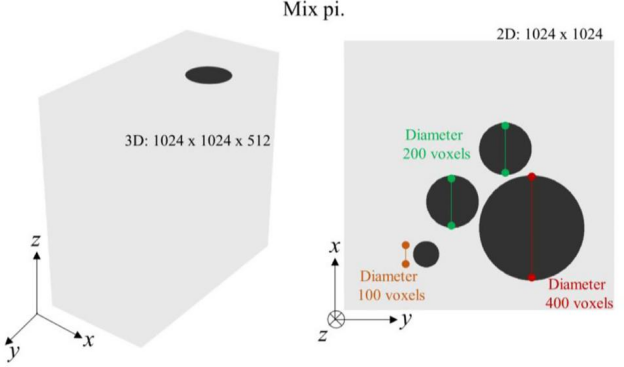
- 2D 岩石:5 个由二维岩石结构沿流动方向延伸得到的三维结构;

- 球体填充:1 个在 x、y、z 方向上都是一组相同球体的三维结构;
- 3D 岩石:5 个硅质碎屑岩的三维数字岩石,分别来自 Berea(Rock 1 和 Rock 2)、Fontainebleau(Rock 3 和 Rock 4)和 Castlegate(Rock 5)。

数值求解器
数值求解器的模拟结果与实验室测量之间的差异原则上可以产生于数字岩石工作流程的每个步骤中,从样本选择、成像、图像处理到求解器本身。而在本研究中,研究人员只关注求解器。因此,实验室测量应仅被视为名义上的参考,所有求解器的结果都是标准化的。重点是对于同一岩石结构,不同求解器的结果如何不同。
本研究中采用的数值求解方法大致可以分为五类:
- LBM:格子玻尔兹曼方法
- CFD:计算流体动力学求解器
- VBS:基于体素的直接 Navier-Stokes 求解器
- SAS:半解析求解器
- EMP:Kozeny-Carman 经验模型
结果
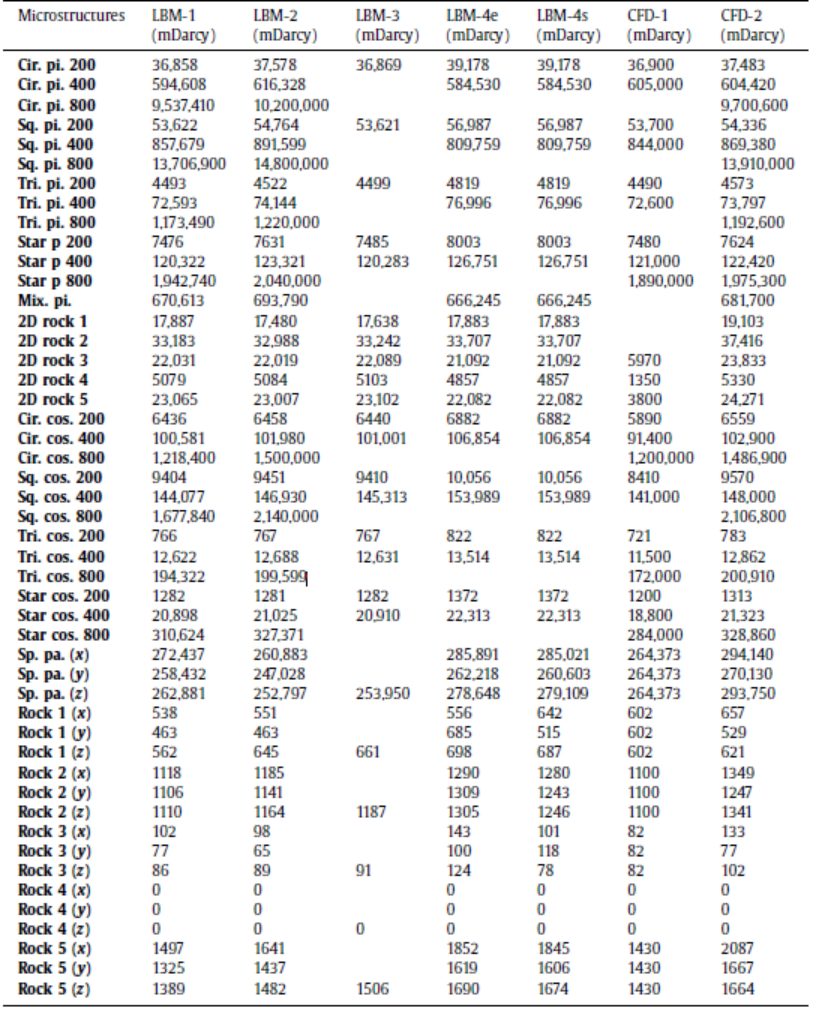
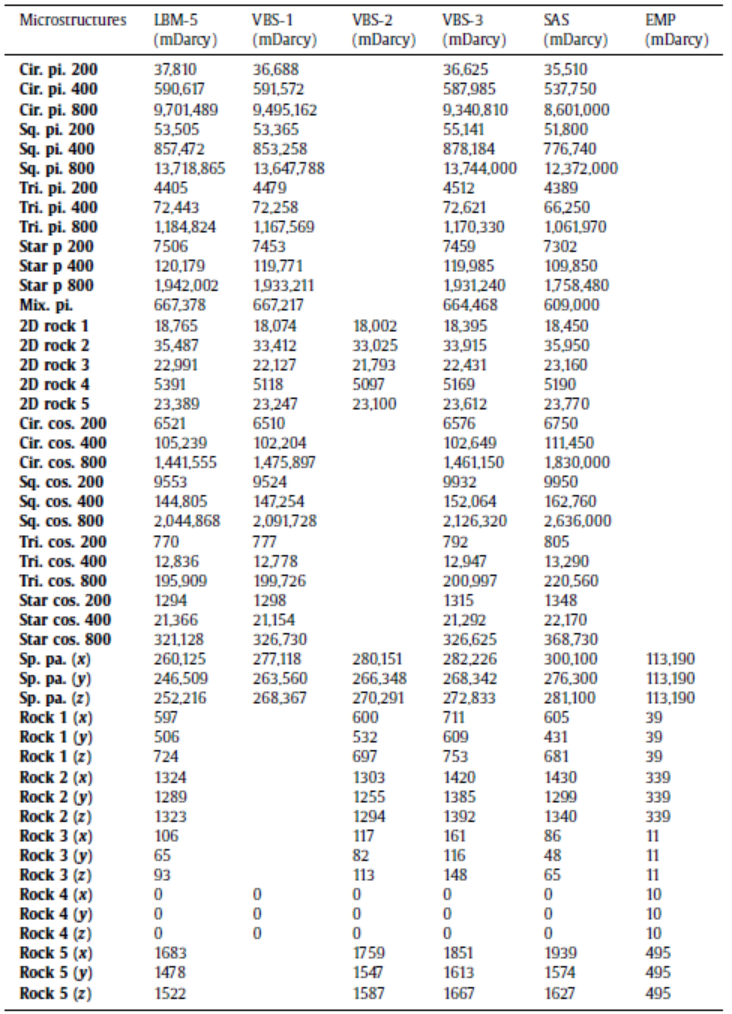
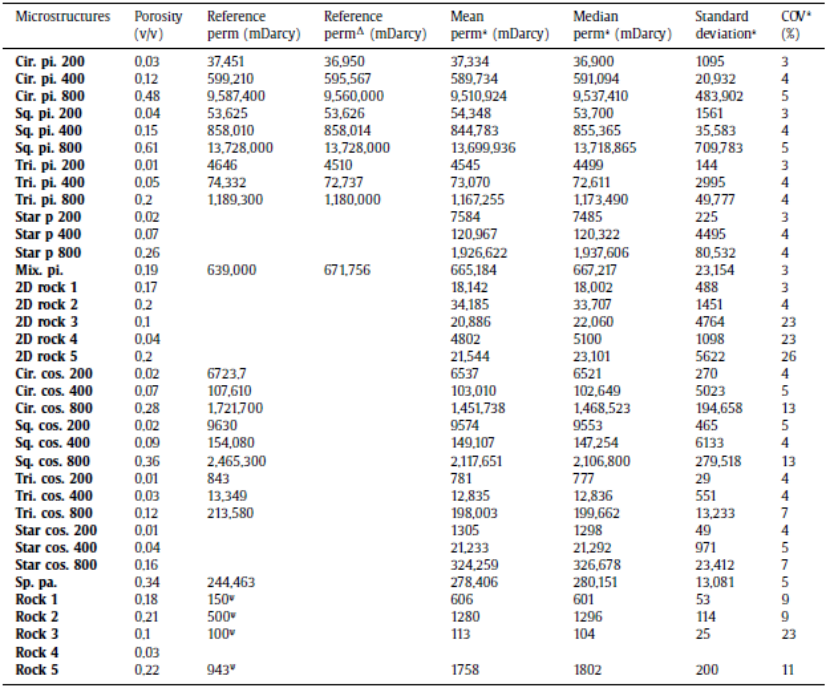
注:COV* 不包含 EMP 方法的结果
根据表中数据显示,使用各种求解器计算的渗透率值与 2D 管道的微观结构非常吻合;2D 岩石的结果存在较大差异,主要是 CFD-1 和 EMP 方法的数值较低,可能由网格划分的复杂性造成。这种差异在 2D 正弦管道中还算适中,对于3D 岩石来说相对较大。
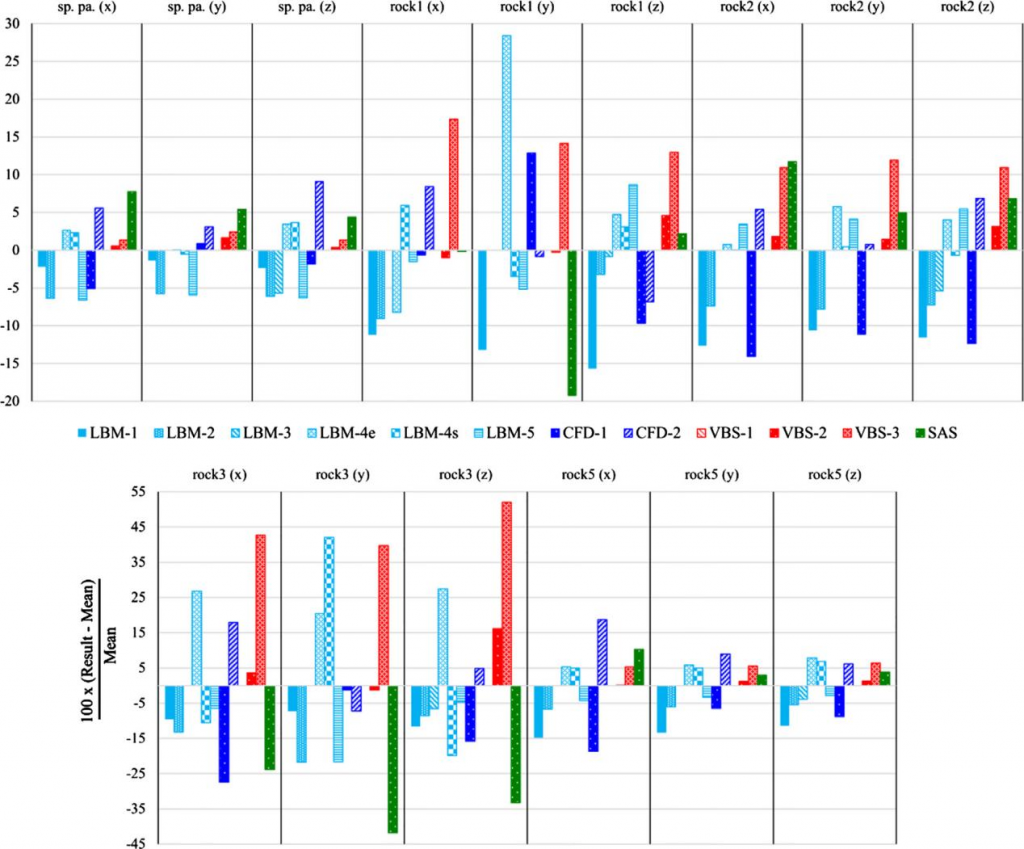
总体而言,CFD 求解器与参考数据的一致性最好,其次是 VBS、LBM 和 SAS 求解器。将数字计算的渗透率与实验室测量进行的比较,在统计上没有显著性。显然,仍然需要更详细的分析来建立对两种方法渗透率估算之间相关性的可靠理解。
结论
用给定体素大小的数字岩石图像来量化最低单相渗透率,任何接近这个极限值的计算方法都必然是错误的,但通过以更精细的分辨率对岩石进行成像来克服这种不确定性是可行的。数值解之间的不一致即变异性,会随着孔隙空间复杂性程度相应增加。总体上,不同求解器对单相不可压缩流体渗透率数值解的差异可归于边界条件、数值收敛准则以及 Stokes 方程离散化的不同。
这项研究还没有完全解决数值结果与实验数据间差异的可能原因,但发现数值模拟计算的渗透率几乎总是高于实验。在未来的研究中,我们将把导致这种差异(或不确定性)的相对贡献联系起来,可能来源于定向尺度升级、micro-CT 成像和流动测试时岩石上不同的应力、成像体素大小、REV 和求解器的选择。
参考
- Saxena N, Hofmann R, Alpak F O, et al. References and benchmarks for pore-scale flow simulated using micro-CT images of porous media and digital rocks[J]. Advances in Water Resources, 2017, 109: 211-235.
