概述
动力学模拟是一种重要的原子级模拟方法,通过求解原子运动的经典力学牛顿方程对相空间进行采样,不仅可以研究体系在相空间的演化过程,还可以通过产生的系列结构(系综)通过统计方法得到体系在非零温度下的各种性质。 动力学过程中的原子间相互作用力则可以通过多种方法求得,可以是密度泛函理论,也可以是经验力场。
使用QuantumATK进行材料动力学模拟
- 可以用多种能量-力计算方法
- 密度泛函理论(DFT-LCAO 和 DFT-PlaneWave):支持几千原子级别超大体系的计算
- 半经验量子力学模型(SemiEmpirical):支持密度泛函紧束缚近似(DFTB)
- 经验力场(Forcefield):支持几百种经验势参数(含ReaxFF)
- 机器学习力场:高效率平衡DFT的精度和力场的速度
- 支持多种系综和理论方法
- NVE velocity verlet
- NPT with stress mask
- NPT/NVT(Berendsen)
- NPT Melchionna
- NPT with stress mask
- Langevin
- 多种方法初始化速度
- 灵活的结构限制固定部分原子
- 分别固定 x、y、z 坐标
- MD 过程中固定质心
- 限定布拉维格子(可同时设定目标应力)
- 刚性限定原子相对位置关系
- 支持多种动力学方法
- 平衡态分子动力学
- 非平衡态分子动力学(RNEMD)计算热导
- time-stamped force-bias Monte Carlo长时域的动力学方法
- Metadyamics(PLUMED):更快的对能量(自由能)面进行采样,获得大范围的结构-能量信息
- 自适应动力学蒙特卡罗方法(adaptive kinetic Monte Carlo):研究结构变化与机理
- 可控制局域温度、设定升温速率
- 所有恒温器、恒压器支持线性升温或降温
- 计算过程中分析
- Python 脚本支持计算过程中分析或添加其他限制条件
- 部分电荷分析
- 可视化原子速度
- 轨迹或单个结构分析工具(同时支持导入 VASP、LAMMPS 结果分析)径向分布、角分布函数
- 速度自相关函数
- 局域质量密度分布
- 配位数分析
- 均方位移
- 最近邻数
- 中子散射结构因子
- 速度/动能分布
- 局域结构(Voronoi)
- 中心对称性
- 从轨迹计算声子态密度
- 使用脚本可以方便的对超大体系的部分原子进行以上各种分析
- 力学性质力和应力(解析 Hellmann-Feynman)
- 弹性常数(应力-应变曲线)
- 局域应力
QuantumATK:高效的动力学引擎
基于QuantumATK高效的DFT、SE和ForceField计算引擎和MD代码的优化,分子动力学计算速度有明显优势。其中DFT、SE、ForceField均支持MPI大规模并行,并获得极大的速度提升。
基于DFT的MD计算速度测试结果
7056原子的分子动力学(水分子):在64MPI并行时,第一步MD耗时4分钟。

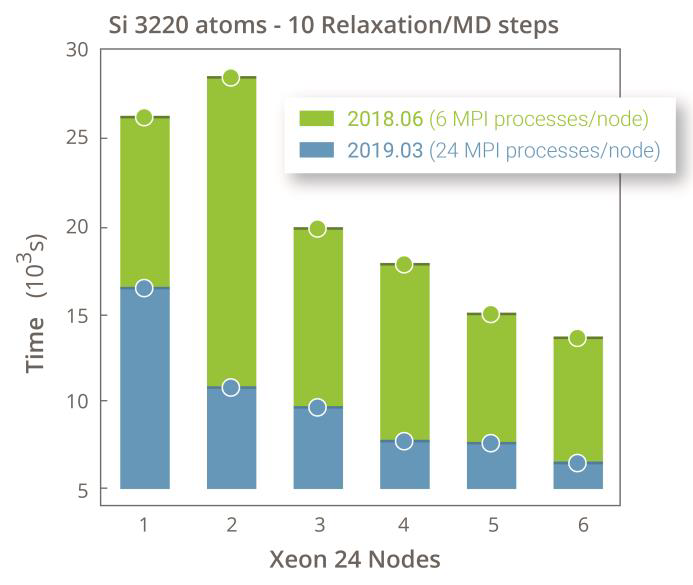
3220原子的分子动力学(硅固体):144MPI进程并行,1步耗时约10分钟。
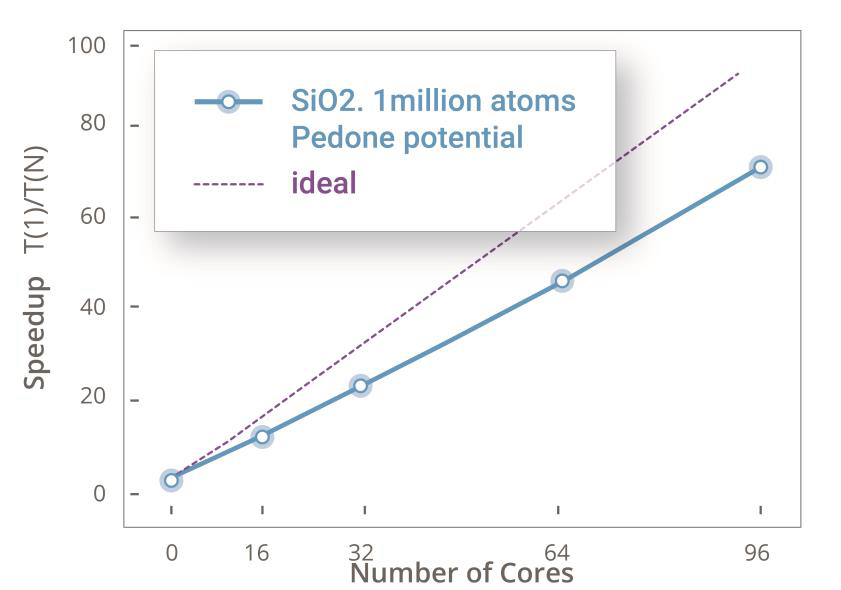
基于ForceField的MD并行加速测试(1百万SiO2原子)
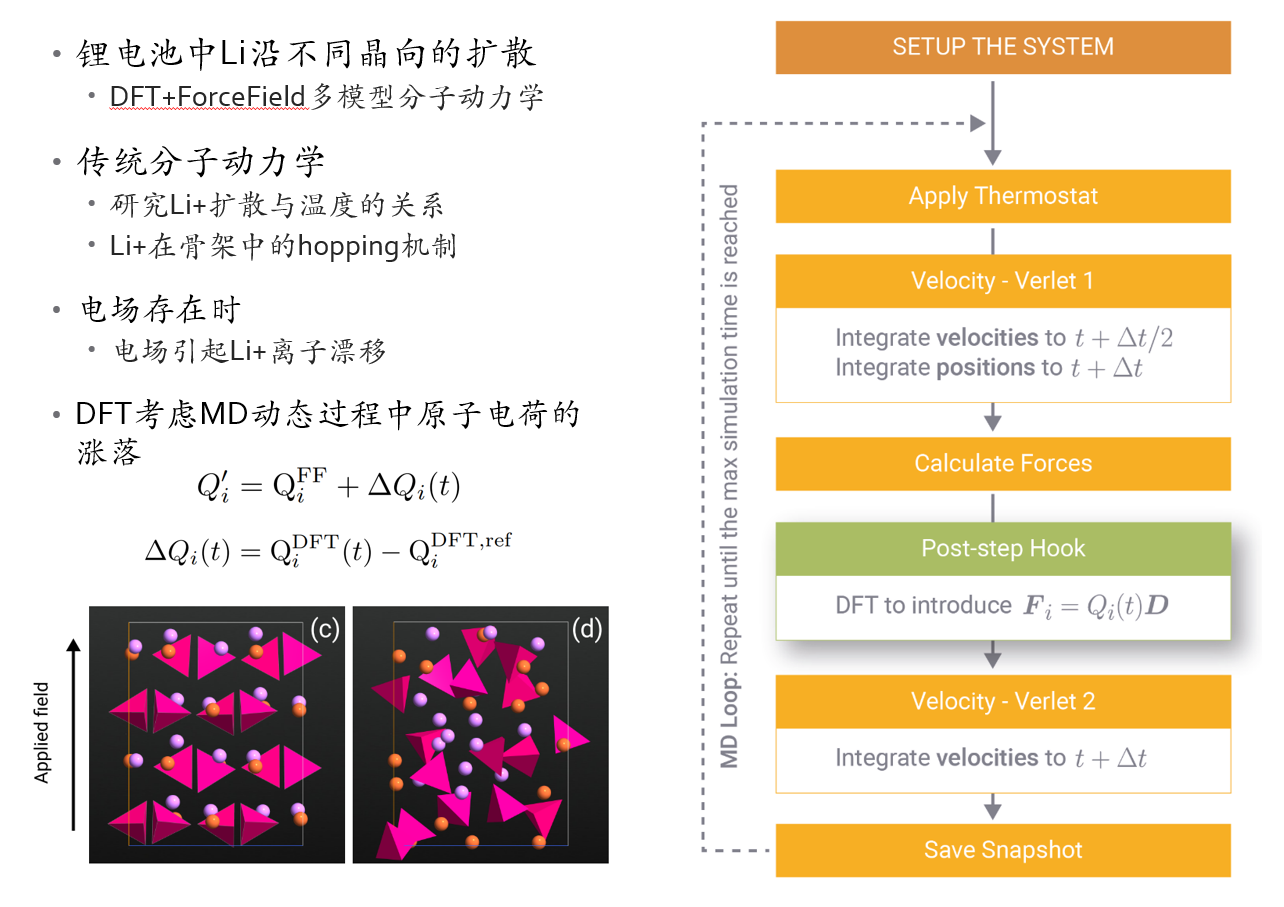
DFT+ForceField混合方法动力学
QuantumATK提供更灵活的分子动力学模拟框架,可以在一个动力学模拟过程中混合使用DFT和ForceField。
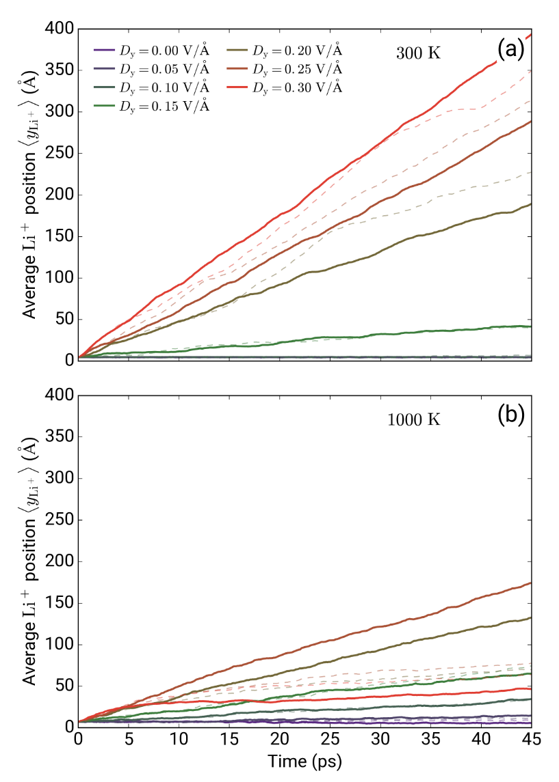
图:LiFePO4中Li在外电场下的扩散动力学模拟。考虑电场的同时,DFT的引入可以反映原子电荷在动力学过程中的涨落。
time-stamped force-bias Monte Carlo方法
使用time-stamped force-bias Monte Carlo方法(基于DFT、DFTB、力场)代替普通的分子动力学,可以研究更长时间的平衡、沉积、无定型化、扩散、快速熔化–退火、对罕见事件采样。模拟过程可以恒定温度,也可以是线性升温降温。
- 与MD类似,但是原子位移使用Monte Carlo方法采样
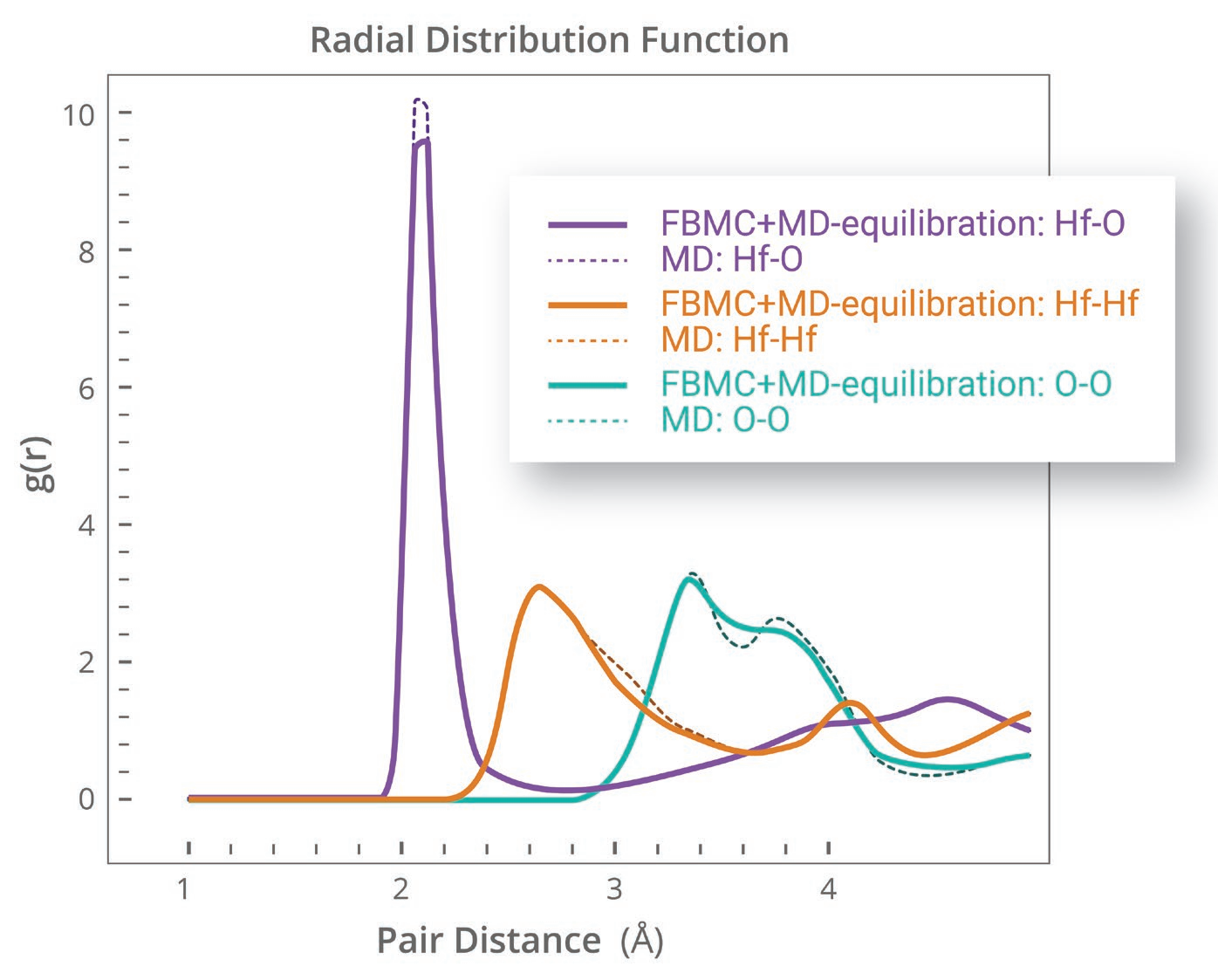
- 将结构在给定温度下平衡并采样(图:HfO2的fbMC与普通MD的结果比较)
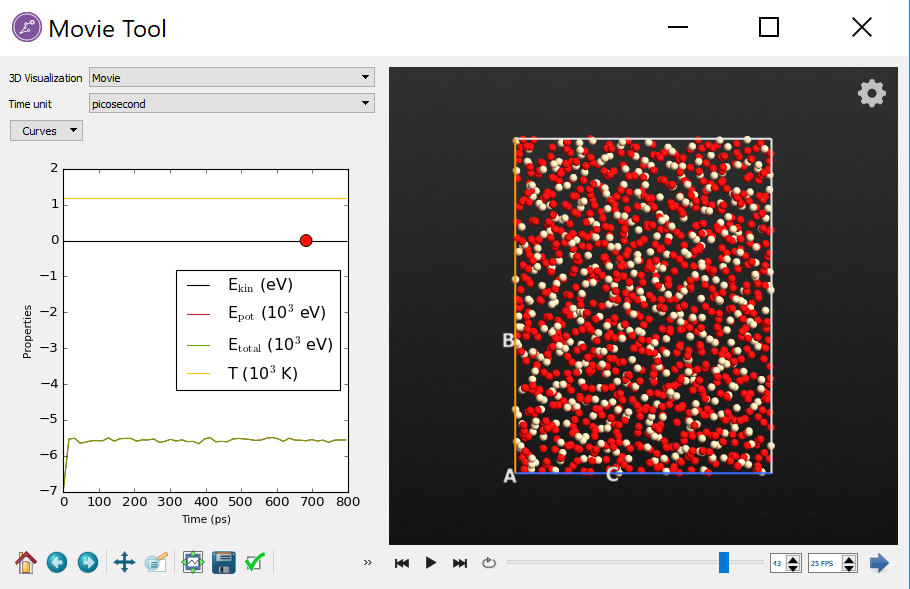
- 模拟时长可以是传统MD的100倍(图:SiO2 的 800 ps fbMC动力学轨迹分析)
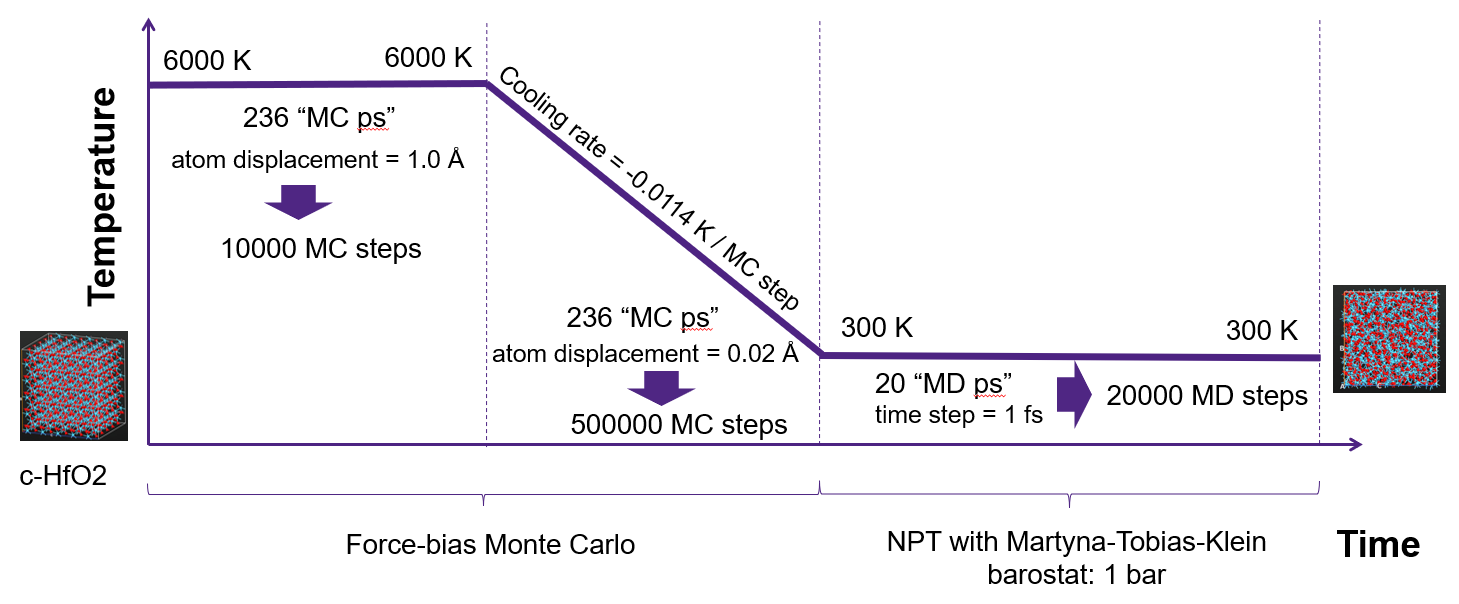
- 与普通MD混合使用(图:fbMC恒温—fbMC降温—NPT MD恒温)
Metadynamics(PLUMED)方法
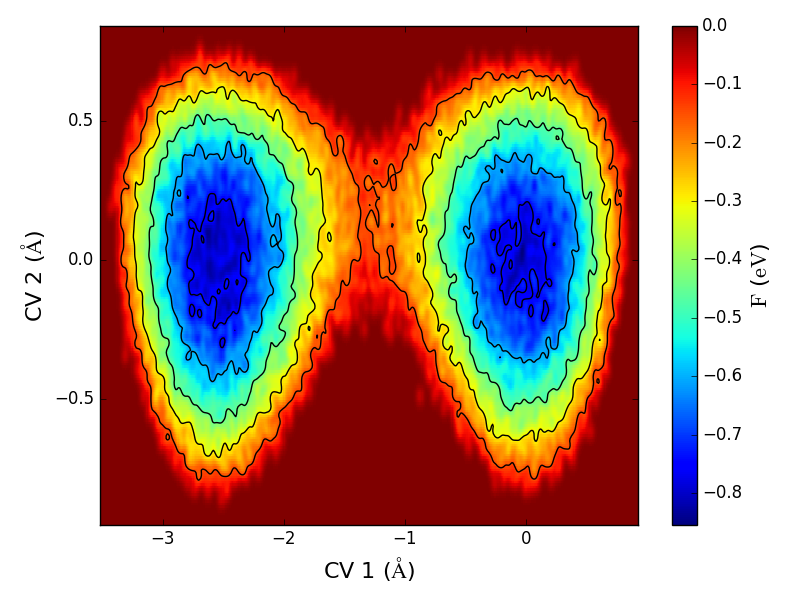
在温度不太高的情况下,分子动力学过程往往会被局限于(自由能)能量面上的一个局域极小值附近采样,这大大限制了分子动力学的应用。Metadynamics则是在普通的MD基础上按一定的模拟时间间隔施加一个人为的势场,促使研究的体系克服势垒从一个较深的局域极小附近离开到另外一个局域极小附近。这种方法大大提高了对能量面的采样的效率。在材料模拟领域,Metadynamics常常用来研究固体的晶态多样性、固体-液体界面、固体中或表面上的化学反应。
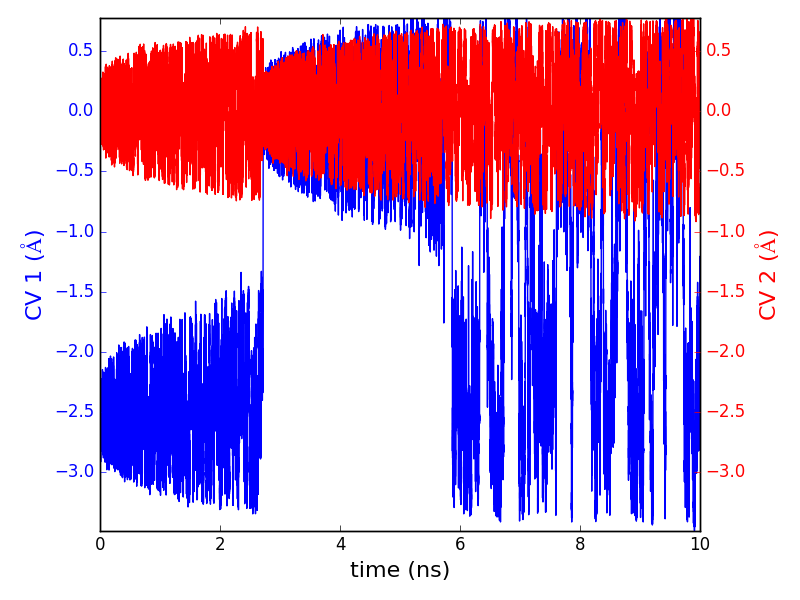
下图:Cu在Cu(111) 表面扩散的能量曲面,图中显示扩散过程中的两个能量极小;扩散过程中原子坐标随时间的变化。
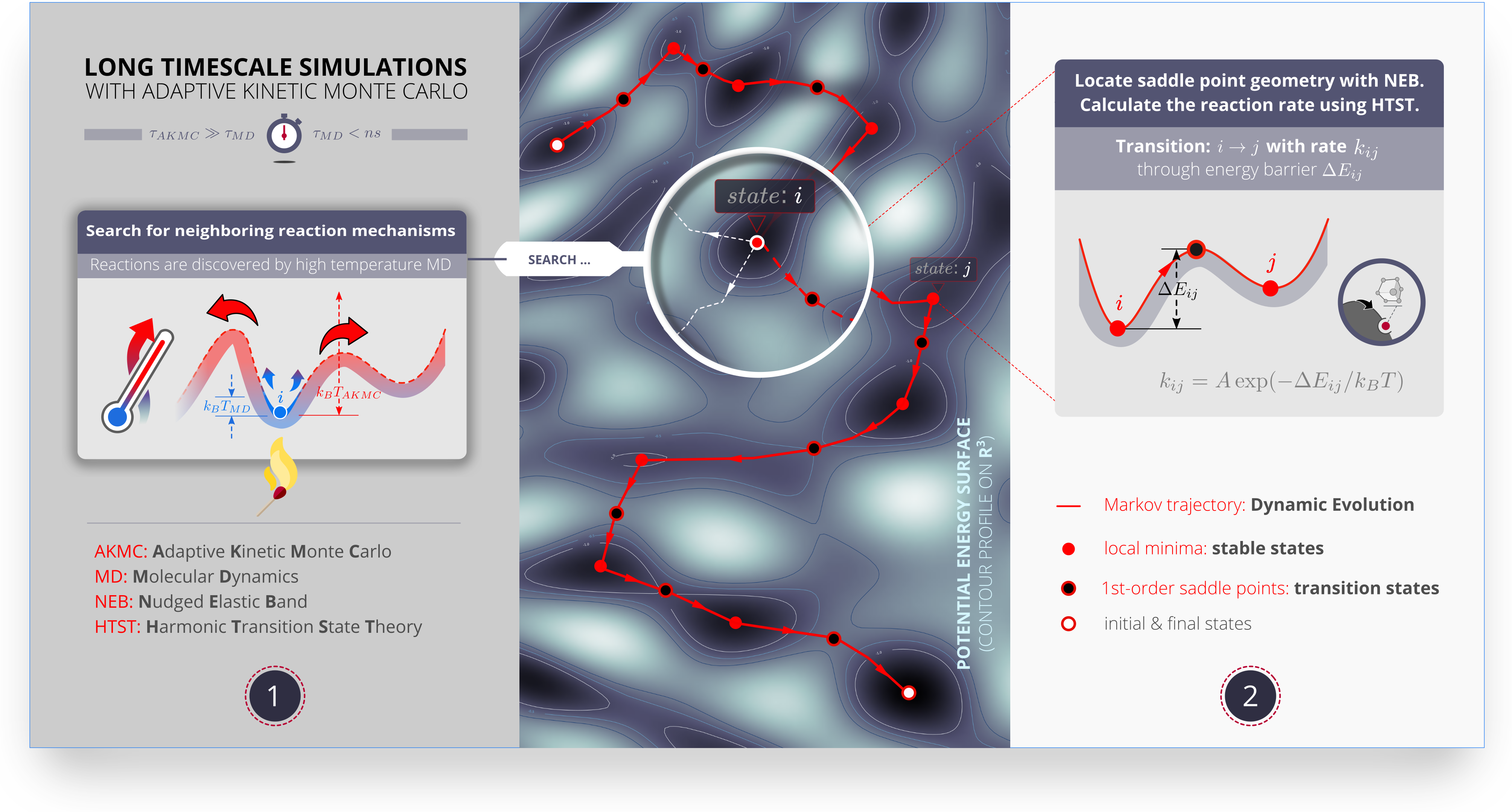
自适应动力学蒙特卡洛(akMC)方法
akMC将高温MD与NEB过渡态搜索结合,是另一种研究固体中结构变化(反应、扩散)过程的方法。这些结构变化过程在统计学上是罕见的事件,因此很难用传统的MD模拟,尤其是与结构变化直接相关的能量面鞍点信息。(图:akMC原理)
akMC可以得到:
- 一系列结构变化形成的Markov链
- 结构变化过程中的每步的势垒和变化速率
具体实例详见下文的“实例与教程”中的链接。
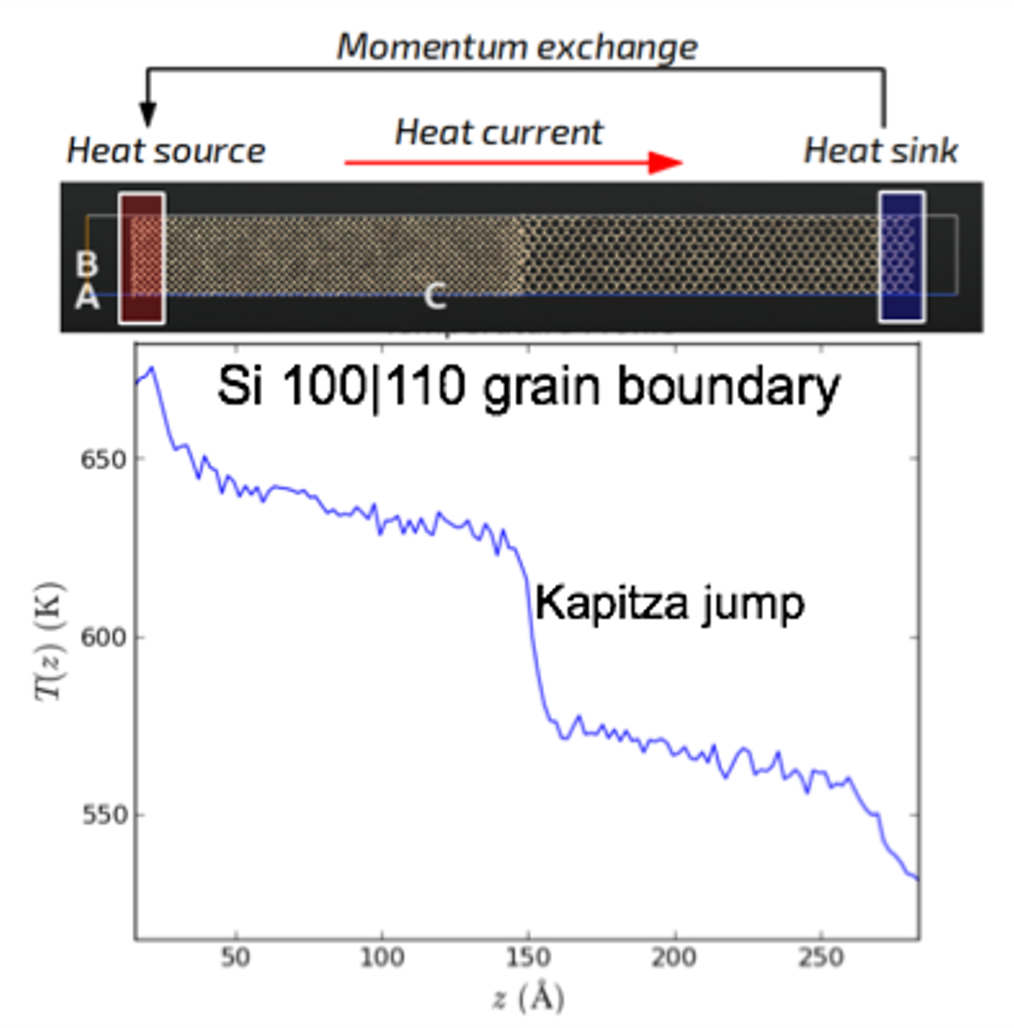
RNEMD:非平衡态分子动力学研究热导
使用非平衡态分子动力学研究材料/界面的热导。下图:Si 100|110界面,通过对两段进行加热和冷却,在体系内建立温度梯度和热流,即可计算出体系的热导。
NanoLab:强大易用的图形界面,让研究者专注于研究,更快获得结果
超大体系的显示和分析,原子数可达百万级
QuantumATK支持高效的图形渲染,可以在普通的主流笔记本电脑上快速、平滑的渲染高达百万原子的体系。
建模工具:方便的构建各种复杂的结构
- 分子、块体、表面、界面、器件建模
- 使用packmol产生初始的分子充填结构
- 使用吸附工具自动创建任意吸附位点、任意覆盖度的的吸附结构
- 使用经验力场产生无定形结构
- 使用多晶建模工具构建多晶模型
- 详见: 【NanoLab建模功能介绍】
设置计算:模块化、流程化设置动力学计算过程
结果分析工具
- 直接由分子动力学轨迹得到体系的各种分布函数和性质
- 径向分布函数
- 速度/动能分布
- 速度自相关函数
- 局域质量密度分布
- 局域应力分析
- 从MD轨迹计算声子DOS
- 配位数分析
- 角分布函数
- 均方位移
- Evolution of average nearest neighbor number with tine
- 中子散射结构因子
- 弹性常数(应力-应变曲线)
- 多种函数重叠作图
- 支持柱状图、线状图
- 显示MD模拟过程的原子速度
- 显示MD动画并支持自定义显示、按帧导出结构,导出动画文件
- 支持导入LAMMPS和VASP的MD结果并进行分析

模拟实例与教程
- 分子动力学基础
- 模拟气相沉积薄膜生长
- 模拟原子轰击石墨烯
- 如何施加单轴和双轴应力
- 添加、组合、修改经验力场
- 生成无定形模型
- 缺陷碳纳米管的杨氏模量
- 非平衡态分子动力学与界面热导
- 液体中扩散现象的分子动力学模拟
- 多晶铜的蠕变
- 使用PLUMED Metadynamics模拟铜空位在Cu111中的扩散
- 锂-硫电池的电压性质
- 液体粘度的分子动力学模拟
- 半导体合金中的空位扩散动力学(AKMC方法)
- Pt表面的岛状结构的形成过程(AKMC方法)
- Pt表面原子的扩散
- 使用主动学习方法产生HfO2结构的MTP机器学习力场
