研究简介
范德华多铁隧道结有望实现小型化、高密度和非易失性存储,在下一代数据存储和存算一体器件中具有巨大应用潜力。福州大学材料科学与工程学院萨百晟课题组联合北京航空航天大学和华中科技大学,采用结合密度泛函理论与非平衡格林函数结合的计算方法,模拟了由铁磁半金属材料 $\mathrm{Mn}_2\mathrm{Se}_3$ 作为自旋过滤势垒,金属材料 $\mathrm{Ti}\mathrm{Te}_2$ 作为电极,铁电材料 $\mathrm{In}_2\mathrm{S}_3$ 作为隧道势垒组成的范德华多铁隧道结器件的自旋输运性质。器件采用双层 $\mathrm{In}_2\mathrm{S}_3$ 作为隧道势垒时可以同时实现显著的隧道磁阻和隧道电阻效应,在非零偏压下,最大隧道磁阻和电阻比率分别可达6237%和1771%。进一步发现在该多铁隧道结内存在四种可区分的电导状态,即仅需一个多铁隧道结单元就可实现四态非易失性数据存储。且通过等效的磁、电开关可以分别控制器件电流的通断和大小,通过搭建多铁隧道结阵列可同时实现逻辑计算和多级数据存储。这些研究结果揭示了该隧道结在存算一体以及多级数据存储器件中的潜在应用。福州大学材料科学与工程学院博士研究生崔舟为第一作者。该研究得到了国家重点研发计划与国家自然科学基金的资助支持。
研究内容
利用QuantumATK软件,以单层铁电材料 $\mathrm{In}_2\mathrm{S}_3$ 作为势垒层,具有金属性质的 $\mathrm{Ti}\mathrm{Te}_2$ 作为电极材料,搭建了如图1所示的器件模型,图1(a)和(b)中显示了 $\mathrm{In}_2\mathrm{S}_3$ 的两种不同极化方向的情况,在考虑铁磁层磁矩的方向后,单层 $\mathrm{In}_2\mathrm{S}_3$ 器件理论上可以实现四种导电状态。图1(c-f),进一步计算了器件不同状态下的透射系数曲线和费米面处的透射谱,并且统计了各种状态下的费米面出的隧穿磁阻率和隧穿电阻率。对于单层 $\mathrm{In}_2\mathrm{S}_3$ 器件最大可以实现448%隧穿磁阻率,但是其最大的隧穿电阻率仅有30%。

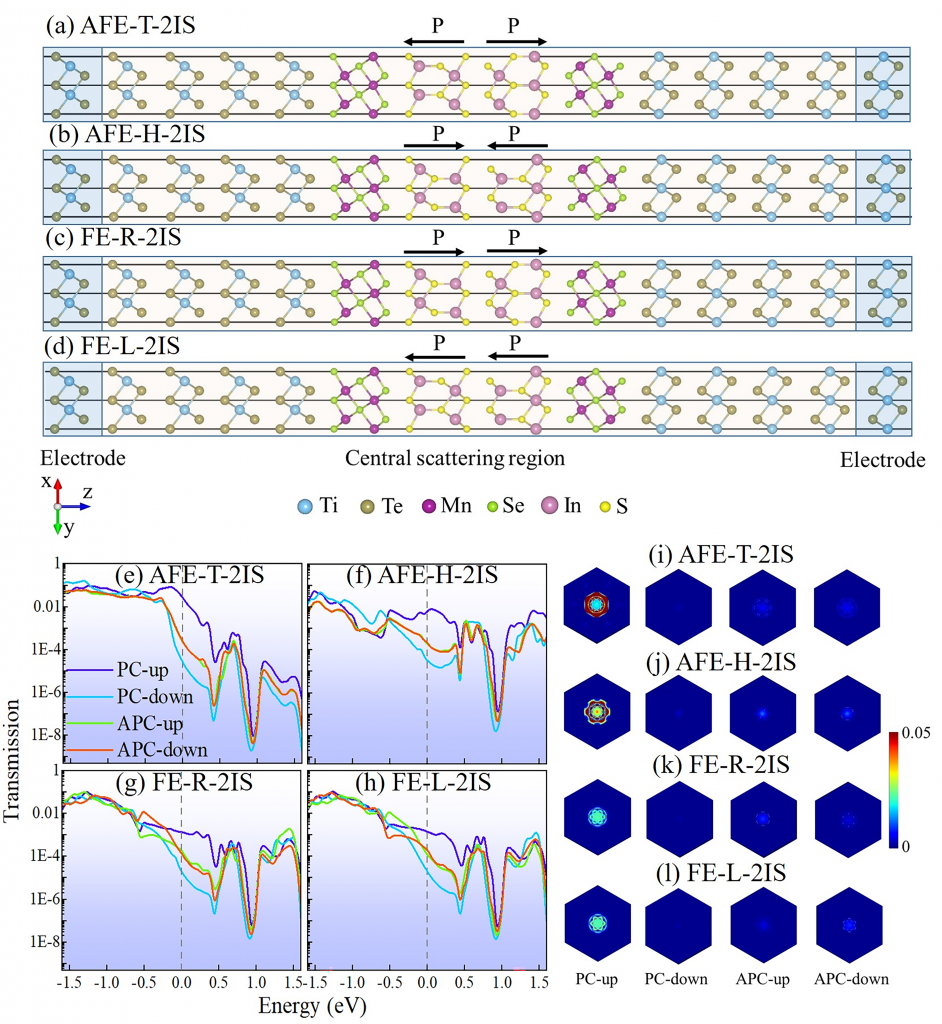
将单层 $\mathrm{In}_2\mathrm{S}_3$ 势垒层替换为双层 $\mathrm{In}_2\mathrm{S}_3$ 后,如图 2 所示,不同状态下的透射系数曲线和费米面处的透射谱具有更明显的差异。对于双层$\mathrm{In}_2\mathrm{S}_3$ 器件可以实现最大的隧穿磁阻率为5698%,最大隧穿电阻率为1771%。从费米能级处的透射谱可以得知,高的隧穿磁阻率和隧穿电阻率主要是由于平行磁阻态下的自旋向上电子的透射能力具有显著差异。
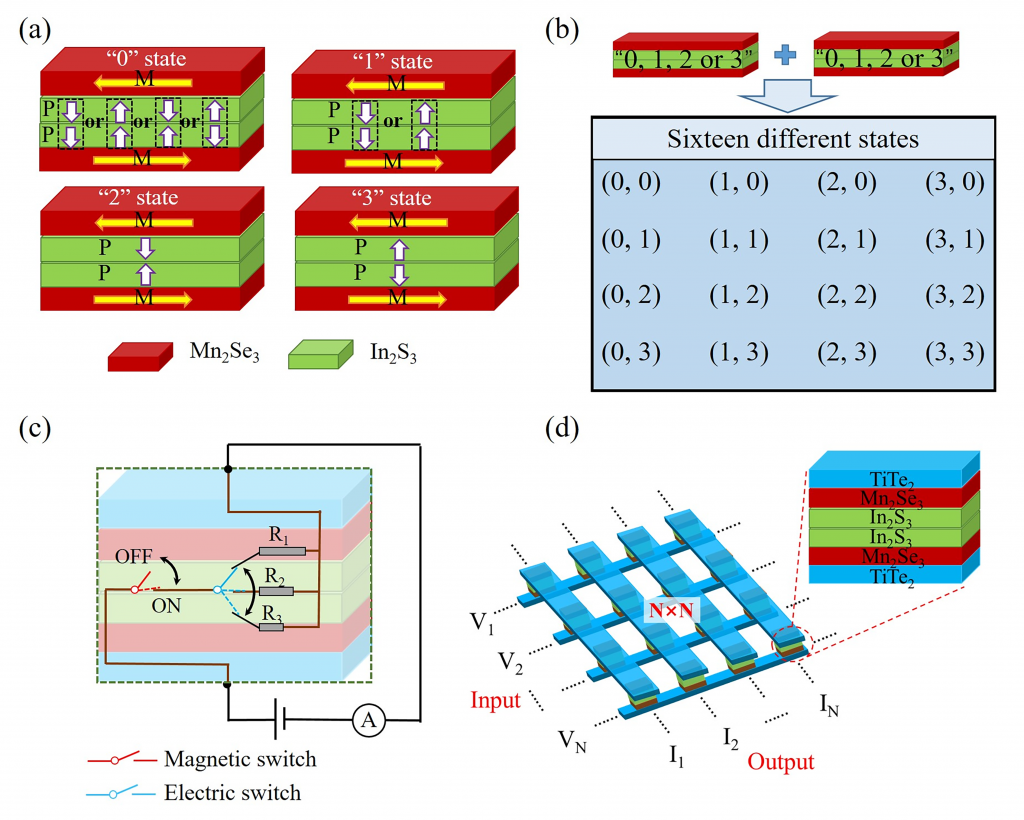
为了进一步探究这种差异的原因,计算了双层 $\mathrm{In}_2\mathrm{S}_3$ 作为隧道势垒的多铁隧道结在各种状态下 $\mathrm{Mn}_2\mathrm{Se}_3$ 和 $\mathrm{In}_2\mathrm{S}_3$ 层的态密度。从图3中可知,由于受到 $\mathrm{Mn}_2\mathrm{Se}_3$ 铁磁层的影响,$\mathrm{In}_2\mathrm{S}_3$ 层在费米面处产生了新的态密度,这是造成器件导电能力不同的主要原因。最后本文阐述了器件可能应用的方向。双层 $\mathrm{In}_2\mathrm{S}_3$ 器件的八个导电状态可以简并为如图4(a)所示的四种可显著分辨的导电状态,仅用两个隧道结单元就可以实现十六种存储状态,用于多态存储,如图4(b)所示。另外,可以将一个隧道结单元等效成为一个磁电开关,用磁场开关控制电路的通断,电场开关控制电流的大小,如图4(c)所示。将多个隧道结单元排列成如图4(d)所示的 N×N 阵列,在输入端加一系列电压,根据基尔霍夫定律和欧姆定律,在输出端可以得到一系列电流,从而完成一次乘法累加运算。由于每个多铁隧道结本身具有数据存储的能力,这样就可以将“存”和“算”集成在同一器件单元上,实现存算一体。

参考
- Z. Cui, B. Sa, K. Xue, Y. Zhang, R. Xiong, C. Wen, X. Miao and Z. Sun., Magnetic-ferroelectric synergic control of multilevel conducting states in van der Waals multiferroic tunnel junction towards in-memory computing, Nanoscale, 2024. https://doi.org/10.1039/D3NR04712a
