基于 XRCT 数值模拟透水路面混合料在现场和实验室的渗透特性

一、概述

透水路面混合料的排水能力通常使用变水头渗透仪在远高于现场预期的水头下测量。在实验室中准确评估渗透性对于避免排水性能的严重高估或低估至关重要，这将会影响设计参数如孔径、出水管和排水系统，以及选择适当的级配和厚度，这些因素直接影响路面的成本和现场预期功能。

计算流体动力学（CFD）和基于 X 射线计算机断层扫描（XRCT）建模的最新研究进展则消除了保持较低水头的实验室挑战。然而，数字图像处理（DIP）和有限体积模拟中的不当表征会导致渗透率测量和流体流动行为的显著误差。过往研究确定了在透水路面混合料中遵循 Izbash 和 Forchheimer 定律的非达西流体流动特性，本研究通过使用先进的基于 XRCT 建模方法比较不同实验室和现场水头下的达西和非达西渗透参数，有助于更好地理解目前实验室测量的局限性，为开发更精确的渗透仪或更好的路面排水设计提供新的见解。

二、亮点

• 开发可以模拟现场水力梯度下流体流动特性的数值模型
• 比较实验室和现场水头下的达西和非达西渗透参数
• 由适当的 DIP 算法和速度获得雷诺数表征流体流动状态特性

三、试样制备和实验

使用单一尺寸和密级配骨料制备三种不同的圆柱形透水混凝土混合物试样，记为 P1、P2 和 P3。每种试样有三个，如表示为 P1-1、P1-2、P1-3。混合物中包含粗骨料、I 型水泥、高效减水剂，水灰比为 0.3。

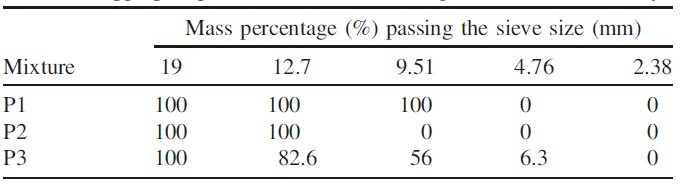
采用 ASTM C1754-12 标准测定透水混凝土试样的有效孔隙率。使用变水头渗透仪测定非达西渗透系数和流动指数，施加从 150 到 25 mm的上游水头并保持恒定的下游水头，通过测量和分析流速获得渗透参数。

四、模拟

4.1 扫描和图像处理

采用西门子 Somatom Emotion 医用 X 射线 CT 扫描设备获得透水混凝土图像，体素尺寸为 0.326 × 0.326 × 0.7 mm。将扫描数据导入 Simpleware 软件进行图像处理，基于阈值分割透水混凝土试样的固体相和孔隙相，在 Simpleware FE 模块采用 +FE Free 算法生成高质量的四面体网格模型。去除孤立孔隙，使用分水岭算法将连通孔隙结构在喉道处分割为多个较小的孔隙，研究不同透水混凝土试样的平均孔隙网络特性，从而确定雷诺数。

4.2 流体流动模拟

将 Simpleware 软件生成的体积网格模型导入 ANSYS CFX 进行模拟，孔隙结构模型中顶部入口和底部出口采用恒压边界条件，所有其他周围表面均采用无滑移壁面边界条件，采用 NavierStokes 方程和 k − ε 湍流方程模拟流体流动行为。

使用雷诺数 Re 确认不同水头下流体流动状态特性：

Re=νd/μ_k

其中，v 是特定流量或渗流速度，d 是平均有效孔径；μ_k 是流体运动粘度。平均有效孔径是通过 DIP 算法确定，忽略这些算法及阈值算法的重要性会导致孔隙网络特性和雷诺数计算出现重大错误。需要强调的是，如果使用平均速度（渗流速度除以有效孔隙率）而不是渗流速度将会导致雷诺数估算过高和流态描述错误。流体流动状态的表征遵循：

• 达西流态：R_e < 1
• Forchheimer 流态：1 < R_e < 150
• 后 Forchheimer 流态：150 < R_e < 300
• 完全湍流：R_e > 300

五、结果与讨论

5.1 模型验证

比较实验和基于 XRCT 模拟方法获得的有效孔隙率、非达西渗透率和流动指数。有效孔隙率的误差在 −1% 至 30%（P3-3 除外），非达西渗透率系数的误差在 3% 范围内。与之前其他数值研究相比误差要低得多，这种改进可归因于 DIP 算法的适当使用和湍流建模。流动指数在 0.44 至 0.53 范围内，表明流体流动处于湍流状态。总体而言，基于 XRCT 开发的模型和 DIP 算法能够预测流体流动特性，并研究不同水力梯度对不同透水混凝土混合物的达西和非达西渗透特性影响。

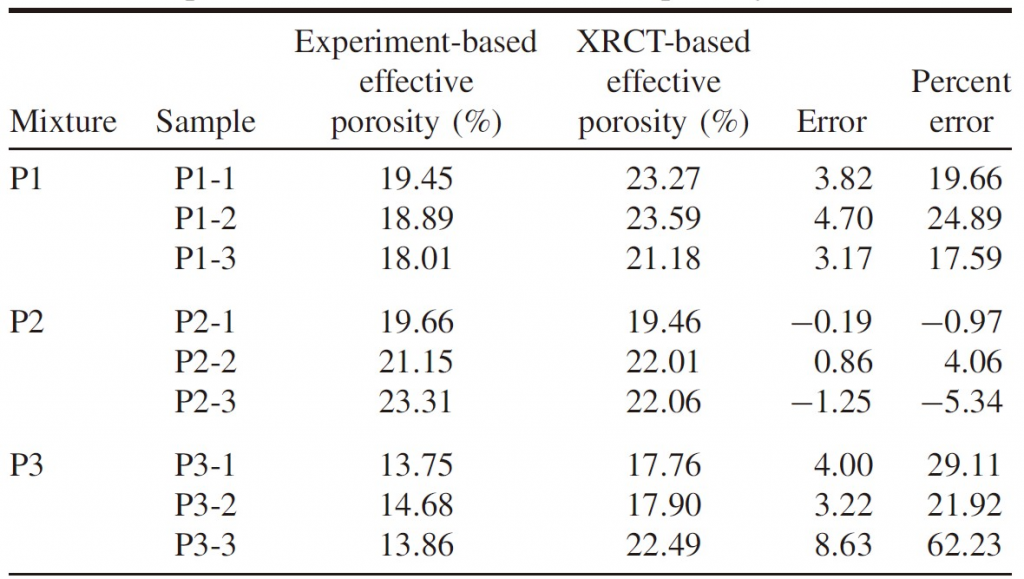
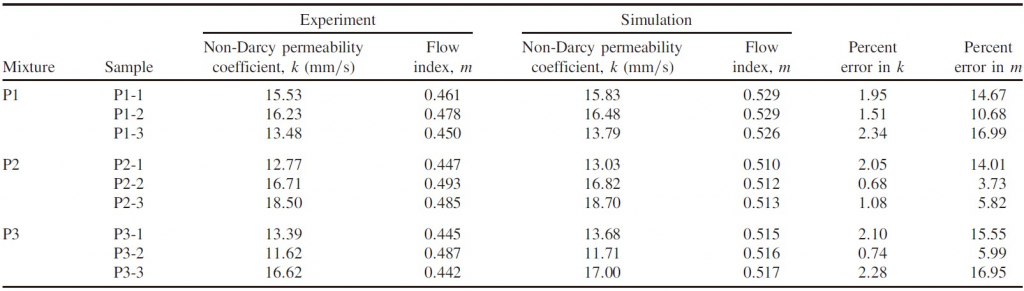
5.2 渗透参数比较

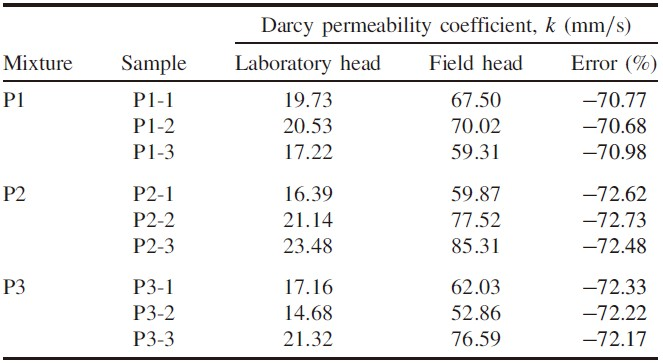
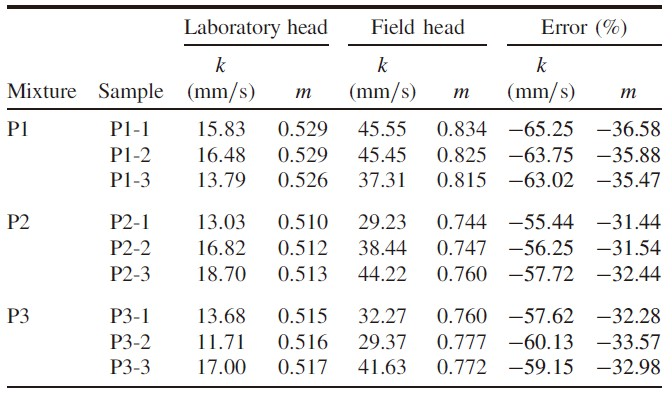
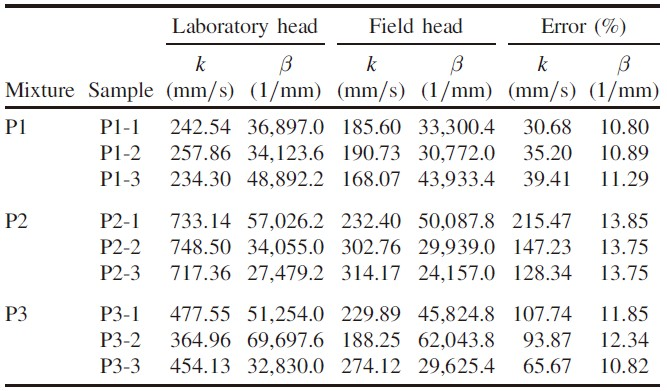
对现场和实验室水头下获得的渗透参数进行比较：达西方程不适合不同水头范围内的流动状态，这也与过去关于流体流动非线性的实验和数值研究结果一致；非达西方程（Forchheimer 和 Izbash）则可以很好地拟合不同水头范围内的流动状态。

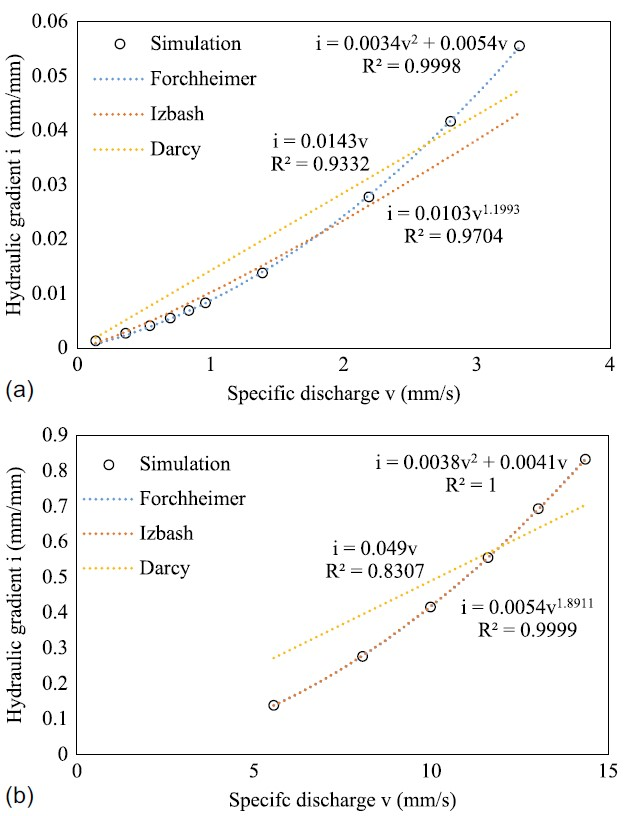
与现场水头相比，使用实验室水头会导致 Darcy 方程和 Izbash 方程的渗透参数被严重低估，而 Forchheimer 方程的渗透参数被高估。随着水头范围的增加，平均流动指数 m 从 0.5（实验室） 增加到 0.8（现场），表明现场水头下为过渡状态，实验室水头下为湍流状态。研究结果强调了水头范围对流动行为的影响，必须使用非达西渗透参数在现场水力梯度下对渗透特性进行适当的评估。

5.3 流体流动状态表征

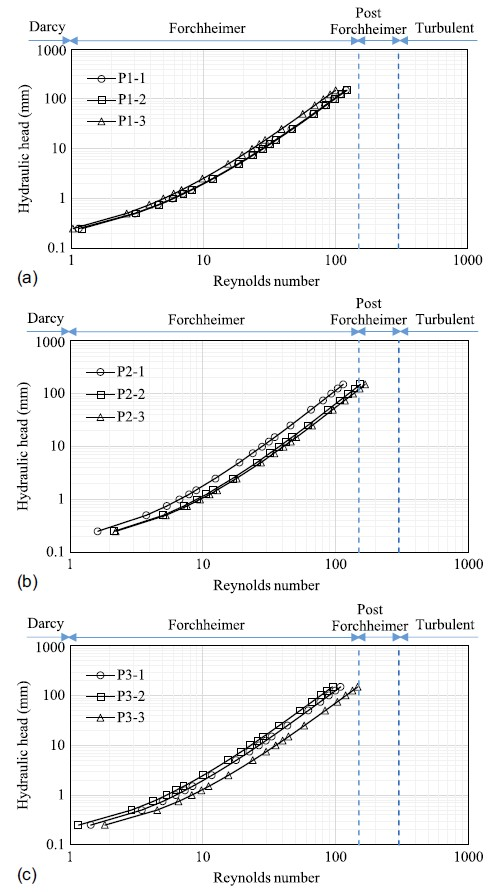
透水混凝土混合物中的流动状态在实验室和现场水力梯度下都表现出流动特性的非线性：

• 随着水头数值的降低，雷诺数也随之降低，代表了所有透水混凝土试样的流动状态变化。
• 大多数试样的雷诺数均在 1 到 150 的范围内，即 Forchheimer 流态；P2-2 和 P2-3 除外，这两个试样的雷诺数略大于 150，为后 Forchheimer 流态。
• 证明达西定律（R_e < 1）在较低水头下不存在。
• 与骨料尺寸较大的试样 P2 相比，试样 P1 表现出较低的雷诺数。

六、结论

本研究旨在探索实验室和现场水头对各种渗透参数如 Darcy、Forchheimer 和 Izbash 参数的影响，使用基于 XRCT 的数值建模量化不同透水混凝土混合物在现场水力梯度下的流态特征。通过实验对主要孔隙网络特性进行验证，针对不同的流体流动方程对各种透水试样在实验室和现场水力梯度下的渗透特性进行评估，最后使用精确的 DIP 算法对流体流动状态进行表征。

• 实验室现有的渗透率测量装置无法复制实际的现场条件（在较低的水头下）。
• 与现场水头相比，使用实验室水头会造成 Darcy 和 Izbash 方程渗透参数的严重低估、Forchheimer 方程的高估。
• 非达西方程非常适合评估现场水力梯度下的透水混凝土流体流动分析。
• 透水混凝土混合物中的流体流动行为是非线性的，且在实验室和现场水力梯度下都表现出过渡流态。

本研究结果强调了基于 XRCT 的建模在弥合实验室和现场渗透特性之间差距方面的重要性，从而增强对透水路面非达西渗透特性的理解。该方法可能有助于工程师为全尺寸透水路面设计有效的排水系统，未来的研究应侧重于实验室和现场水头对透水路面排水设计各个要素的影响。

七、参考

• Jagadeesh A, Ong G P, Su Y M. Bridging Field and Laboratory Permeabilities of Pervious Pavement Mixtures Using XRCT-Based Numerical Modeling[J]. Journal of Materials in Civil Engineering, 2024, 36（4）: 04024026.