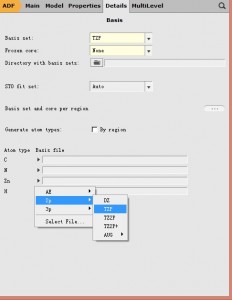
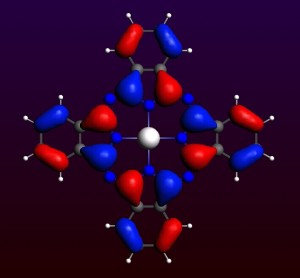
参考文献:Ground and Excited States of Zinc Phthalocyanine Studied by Density Functional Methods, G. Ricciardi and A. Rosa, E. J. Baerends, J. Phys. Chem. A 2001, 105, 5242-5254
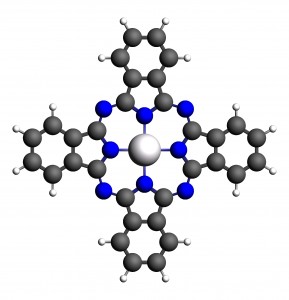
锌酞菁本身具有荧光性,本文计算了锌酞菁的基态和激发态性质。
1, 在ADFinput中画好这个分子的大致模型后,使用ADFinput的自动对称化工具(窗口下方的五角星),将该分子自动往最靠近的高点群调整,如果没有达到要求的D4h群,则稍微调整原子的位置,反复几次,就可以达到最高的D4h群。
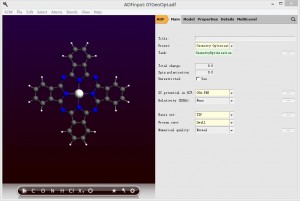
2, 按照文章的流程,我们首先进行几何优化,参数如图中所示:
有几点值得说明:
1) 几何结构优化本身,对泛函、基组、积分精度等参数不太敏感,简而言之,不同的参数,优化得到的几何结构通常差别很小。很多时候,即使电子占据方式不正确,也能优化出很可靠的几何结构。因此,对于大分子在做几何结构优化的时候,我们通常会用很差的参数去优化,例如使用LDA、DZP、Frozen core Large、低积分精度(例如4)等等去优化,这样能够很快收敛。然后将收敛后的几何结构使用高精度参数再优化一遍。这样看起来稍微麻烦,但实际上能够节省大把的时间。而且修改参数重新优化的操作,在ADFinput里面非常方便。例如优化结束之后,ADFinput会提示要不要把优化后的最新的结构更新进来。这时候,当然选择“yes”,然后修改参数,另存,重新优化就可以了。另外值得一提的是,在不设置对称性的情况下,倘若分子的基态具有对称性,例如CO2具有D∞h的点群,那么即使初始结构非常不合理,例如只有Cs群。使用ADF优化(对称性设置不需要修改,使用默认设置)之后,能够自然地得到D∞h群的结构。而其他流行量化软件在这方面则非常困难,甚至不可能做到。
2) ADF中SAOP泛函(确切的说,是一种有效势,没有对应的能量泛函)对于激发能的计算,可靠性往往比其他泛函好,尤其是对于高激发态,得到的结果往往比其他泛函好。但SAOP泛函不支持结构优化,因此我们使用PBE泛函——一种结构优化方面,普适度远高于B3LYP的泛函。
3) 由于该体系具有D4h点群的对称性,因此默认即会采用这样的对称性。而由于对称性的使用,会大大降低计算时间。用一个比喻来说明:D4h分子,有8个区域是等价的,因此计算的时候,只需用计算其中一个区域就够了(这是一个比喻)。实际上在该对称性下,计算最耗时的Fock-like矩阵对角化的部分,原先需要对角化整个矩阵,而现在,整个矩阵(维度非常大)的对角化就变成了10个对角线上的小矩阵的对角化。这12个小矩阵分别是不可约表示A1.g、A2.g、B1.g、B2.g、E1.g(二重简并)、A1.u、A2.u、B1.u、B2.u、E1.u(二重简并),其中E1.g、E1.u对应的小矩阵有两个,本征值是一样的,因此解一遍即得到2个小矩阵的本征值。
通过如上的理论,计算量会比不使用对称性的情况下,降低几十倍,因此计算时间也会缩短几十倍。对于这样大的一个体系,在普通台式机上(4核),十几分钟即可完成高精度的优化。
4) 另外,由于ADF的并行化做的很完善,并行效率非常高,因此对于大体系的计算,只要有足够多的计算资源,并行起来运算,速度是非常快的。例如一个200原子的Si、O、H体系,使用metaGGA进行高积分精度的激发态计算,在128核集群上,也只需要大约十几分钟。目前计算金属团簇、大分子(1000原子-2000原子),ADF非常流行。
3, 对比优化结果
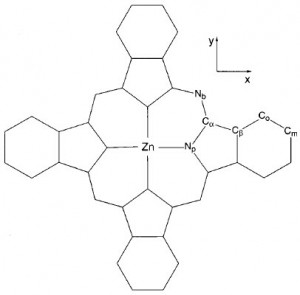
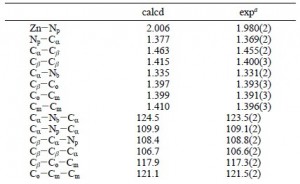
关于几何结构,文献中报道的计算结果和实验结果,如下图所示:
由于D4h点群对称,因此上述表格中的参数,就可以完全确认整个分子的结构。测量Zn-Np的键长(按住Shift键,然后鼠标分别点击两个原子,窗口右下角即显示键长):2.010埃。
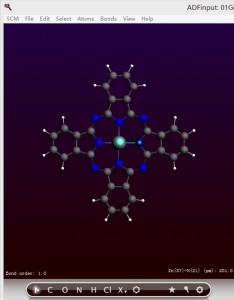
与文献中计算数值相差0.004埃。这是在误差许可范围内的。实际上相差0.02埃左右,都是可以接受的,能级、激发能对键长也同样不很敏感。
另外对应的几个键长也都相差在0.01埃以内,键角(按住Shift键,然后按顺序选中三个原子,右下角即显示键角;二面角的情况类似,按顺序选中4个原子即可)相差在1度以内,这都被认为是相等的。
4, 基态计算
优化结束后,ADFinput提示是否要更新结构:
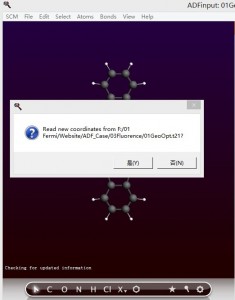
选择yes,则自动刷新结构。此时设置参数为单点计算的参数,如下:
注意此时计算的泛函改为了SAOP,此处基组的冻芯(Frozen core),也更改为不冻芯(因为SAOP不支持冻芯近似)。这与文献中略有差别:文献中基态计算使用了冻芯,其中C和N元素,将1s轨道冻结(如下图所示——点击Basis set选项右方的“…”即可进入该界面,对基组进行详细设置);
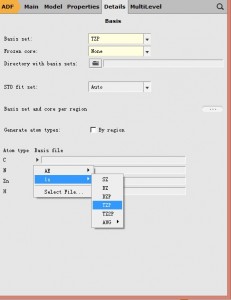
注意 以上图示为文献中的选项,但本次计算,并不做这样的设置,而使用了主面板的Frozen core none的选项,也即“AE”选项,表示All Electron,即进行全电子计算,不做冻芯,所有电子参与自洽迭代。
保存、运行,在4核台式机上,5分钟完成任务。
5, 结果比对
因为文献中使用了冻芯近似,而本计算则使用全电子计算。因此电子数会比文献中多,轨道的序号也会略有差别。不过我们能够很轻易地分辨出对应关系。文献中的能级能量及排序如下:
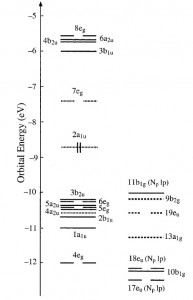
注意上图,由于-10eV到-13eV区域能级过于密集,因此分开两列显示。
我们查看的能级图,如下:
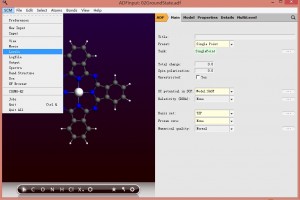
得到能级图如下,选择菜单Axes-Unit-eV,将能级用eV来表示,以保持跟文献一致。否则会使用默认能级单位是Hatree (1Hatree = 27.2113845 eV)。
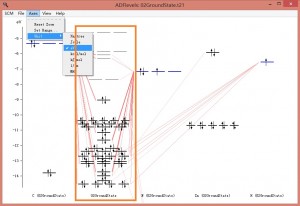
上图中,第二列(名字在下方:02GroundState,为整个任务的名字)为整个分子的能级,左方和右方的列,名字以元素符号开头,例如第一列C(02GroundState),表示该列为C原子的能级。右方的N、Zn、H类似。这些原子轨道(如果使用片段的话,则为片段轨道),如何构成整个分子轨道,这种关系可以从上图大致看到。当鼠标移动到某个能级上,则能看到该能级的情况,例如鼠标放在分子的最高占据轨道(HOMO)上:
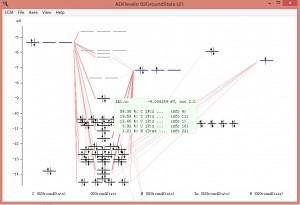
显示该能级的能量为-9.044389eV,占据数为2.0,分别由C原子的1Pz轨道(占59.38%)、另一个C原子的1Pz轨道贡献19.56%,这些轨道分别来自哪个原子数,可以从对应sfo的序号在02GroundState.out文件中找到。右键点击该能级:
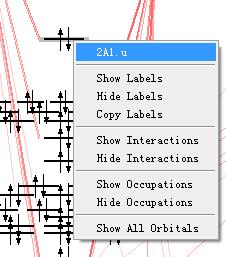
依次对照能级排序,可以发现和文献中的能级排序基本一致(命名规则略有差别)。通过滚动鼠标中键,可以放大或缩小纵坐标。从而理清轨道排序。
值得一提的是:文献中4a2u和19eu两个能级非常接近,从图中几乎无法区分高低,在我们的计算结果中,两个能级也非常接近,在ADFlevel中的标识分别为5a2u和30e1u,能级分别为-10.80eV和-10.92eV。此处单独拿出来说明:化学反应、光学性质,通常与分子的前线轨道关系较为密切,DFT计算的靠内层的轨道,能级排序意义大大减弱,不同的泛函排序可能不同。但这些离HOMO能量稍低的轨道的排序,通常而言,并不影响计算结构、光谱性质。对于吸收光谱而言,即使刚好由于这两个轨道导致,通常也会由于该轨道的对称性的不同而将二者彻底地区分开,从而其排序并不影响最后结果,或者影响非常弱。
但前线轨道的能量排序则很重要,尤其是对光学性质影响非常大。但DFT计算得到的前线轨道通常排序都会比较一致。只是具体数值会有所不同。例如B3LYP的能级间隔要大一些,LDA的能级间隔要小很多。
接下来分析轨道构成:
文献中列举的轨道:
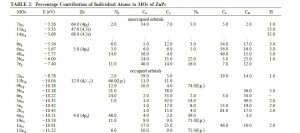
表中第一个轨道7a2u(也就是HOMO之上,第二个a2u的轨道,我们按照这种相对参照的方式,找到对应的轨道更方便,因为前面我们提到了,我们使用全电子计算,而文献使用冻芯,因此轨道的序号略有差别,但不可约表示的名字则是固定的,因为它代表者轨道的对称性),在我们的计算中,对应的是8a2u。能量为-3.69eV。
此处需要说明:在DFT计算中,HOMO附近的一两个轨道,能量与实验值,例如IP和EA是可以比对的。离HOMO较远的轨道,物理意义变差,较高的空轨道,能量基本就不可靠了,因此高激发态的计算,误差也非常大。但一般而言,其轨道的组分变化则稍小,即主要组成成分,基本上是确定的,另外其能级排序也如前面所说一样,意义不大。
我们的计算中,8a2u轨道组分(在ADFlevel界面,鼠标停放在8A2u能级上即可):
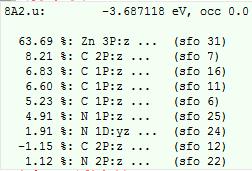
主要成分为Zn的3Pz轨道(sfo 31,即A2u不可约表示的片段轨道中,第31号轨道),百分比为63.69%与文献中64.0%非常接近。该轨道对应的不可约表示为A2u,因此组成它的片段轨道也必须是A2u。在02GroundState.out文件中,我们可以查看该不可约表示(A2u)下的所有片段轨道:
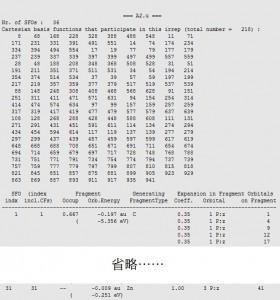
31号片段轨道,来自Zn原子数的3Pz,在level图中也可以看到这种对应关系:

6,激发态与荧光的计算、分析(待续)
更多案例参见费米科技WIKI-ADF
版权声明:本文版权归属费米科技,未经许可,任何其他单位不得用于商业、市场活动。