参考文献:Ground and Excited States of Zinc Phthalocyanine Studied by Density Functional Methods, G. Ricciardi and A. Rosa, E. J. Baerends, J. Phys. Chem. A 2001, 105, 5242-5254
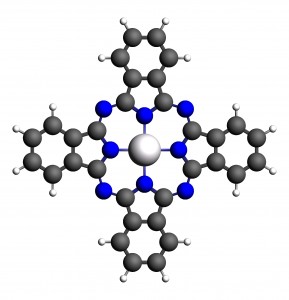
锌酞菁本身具有荧光性,本文计算了锌酞菁的基态和激发态性质。基于前一篇文章的内容,我们此处主要介绍激发态计算、激发态结构优化、激发态频率计算、Franck-Condon因子计算等。
1, 采用优化好的锌酞菁分子结构进行计算:
ADFinput支持比较灵活的分子拷贝、粘贴操作,例如:
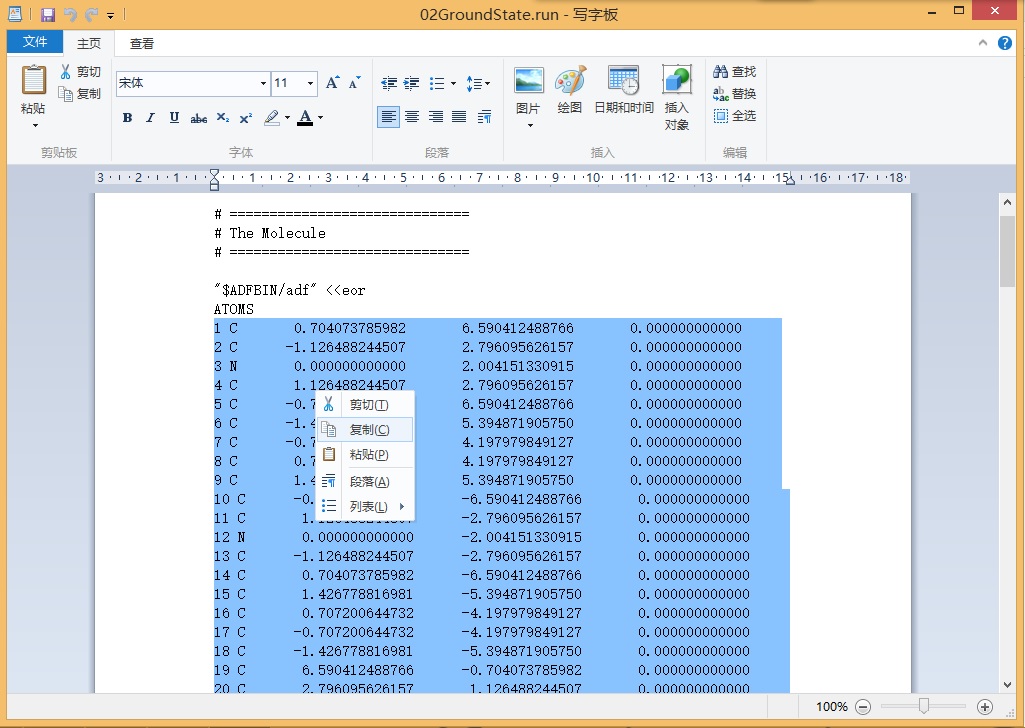
将前一次计算的结构,从*.run文件
或者在上一次计算使用的ADFinput界面里面按快捷键CTRL A(全选),此时ADFinput窗口,所有的原子都被选中,呈高亮状态(当然如果我们希望复制的是一部分原子也是可以的),然后CTRL C(复制)
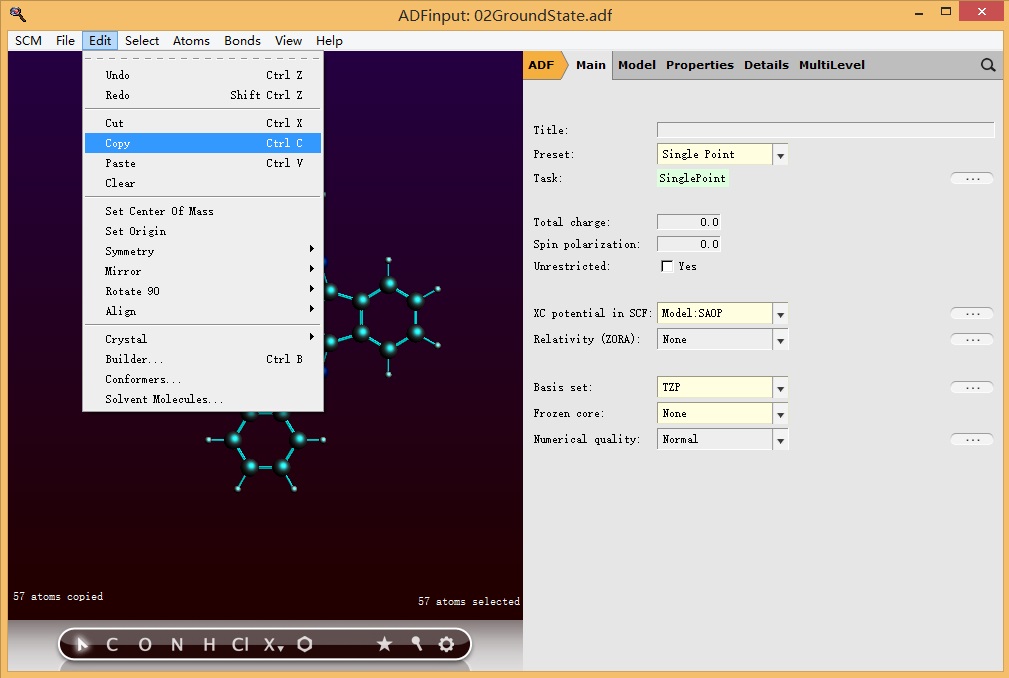
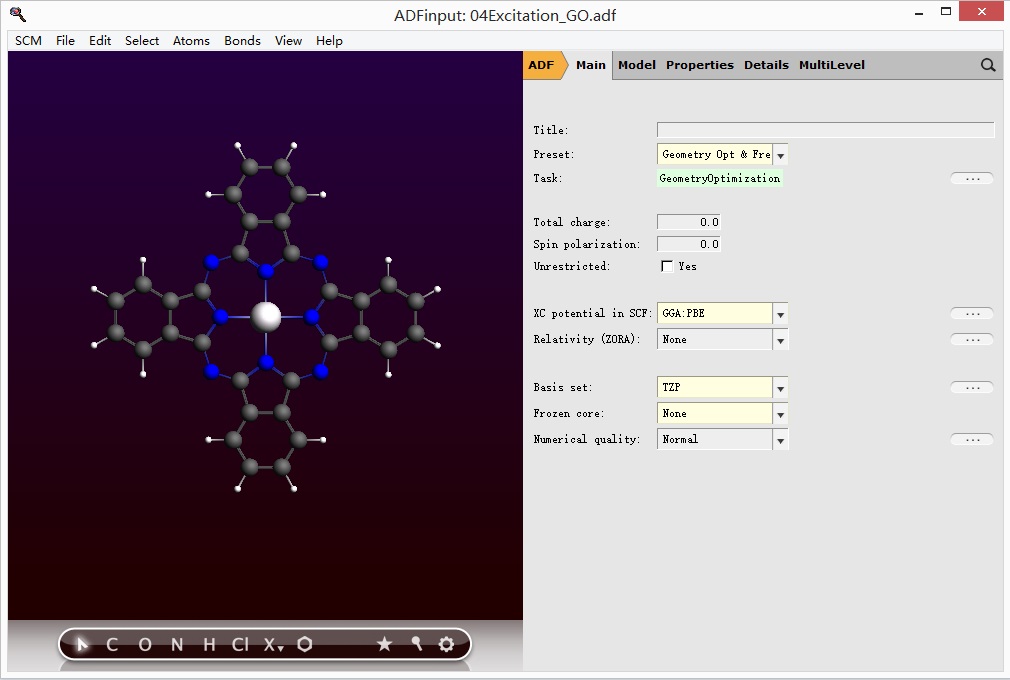
然后在新的ADFinput界面粘贴(或者按快捷键CTRL V),主面板参数设置如下图所示:
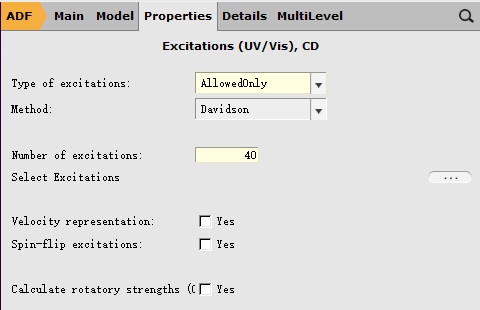
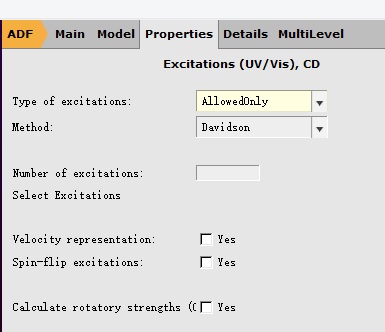
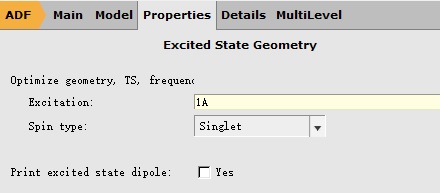
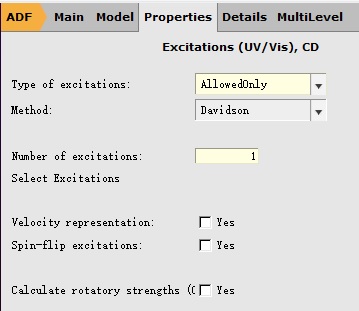
 在Properties-Excitation(UV/Vis),CD设置激发态计算的参数:
在Properties-Excitation(UV/Vis),CD设置激发态计算的参数:
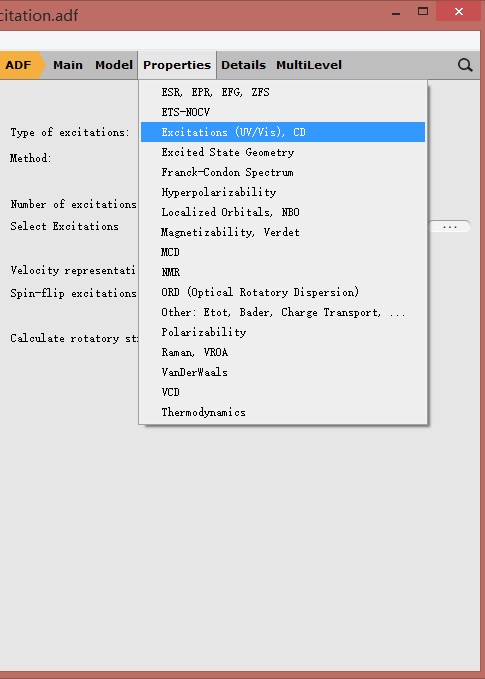
如上图所示,对于激发态的计算,一般而言只需要设置两个参数:Type of excitations和Number of excitations。
前者用于设置激发的类型:对于紫外可见吸收,基态为单重态(S0态),激发态仍然为单重态(S1态);对于此例,选择AllowOnly与选择SingletOnly是等价的。
后者用于设置需要计算的激发态的个数:例如此例中设置为40,表示希望得到S1、S2……S40等40个激发态。该参数一般对于紫外可见吸收,经常也不需要设置,默认值10已经足够。但这个参数对计算速度的影响并不大。
设置完毕,保存任务,例如名为03Excitation。
如果需要计算其他的激发,例如当我们希望计算原子内层轨道电子对X射线的吸收,这时候,可以使用Select Excitations,将需要激发的态指定为内层原子轨道。指定方式非常灵活,可以根据能量也可以根据轨道序号。内层轨道能量或者轨道的序号,从该结构对应的基态计算结果中,可以查找出来,进而进行指定。注意能量单位为Hartree,这是很常用的能量单位,与eV的换算关系:1Hatree=27.2113845eV。
2, 输出结果
提交任务进行计算,计算结束之后,得到03Excitation.t21、03Excitation.out、03Excitation.logfile。这三个输出文件是最重要的输出文件,也是最常用的输出文件,其他输出文件则一般很少用到。查看吸收谱:
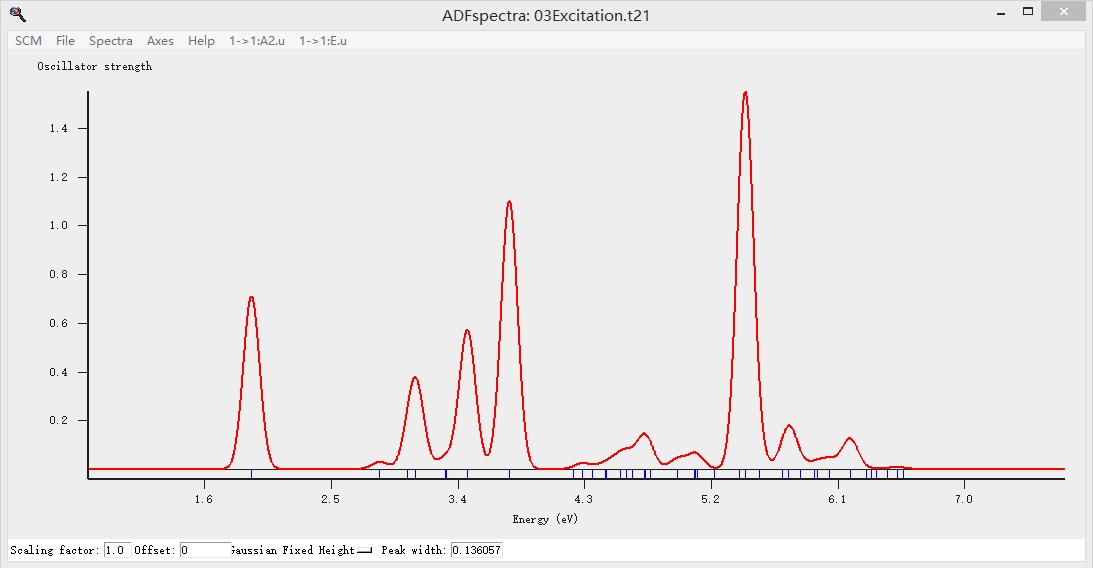
显示吸收谱如下:
SCM-Spectra可以显示所有的谱,因为当前计算的是吸收谱(或者说激发态),因此Spectra自动显示吸收谱,如果计算的是其他的谱,就会自动显示其他谱,如果同时计算了多种谱,可以通过该窗口中的“Spectra”下拉菜单,在不同的谱中切换:
3, 激发态分析:
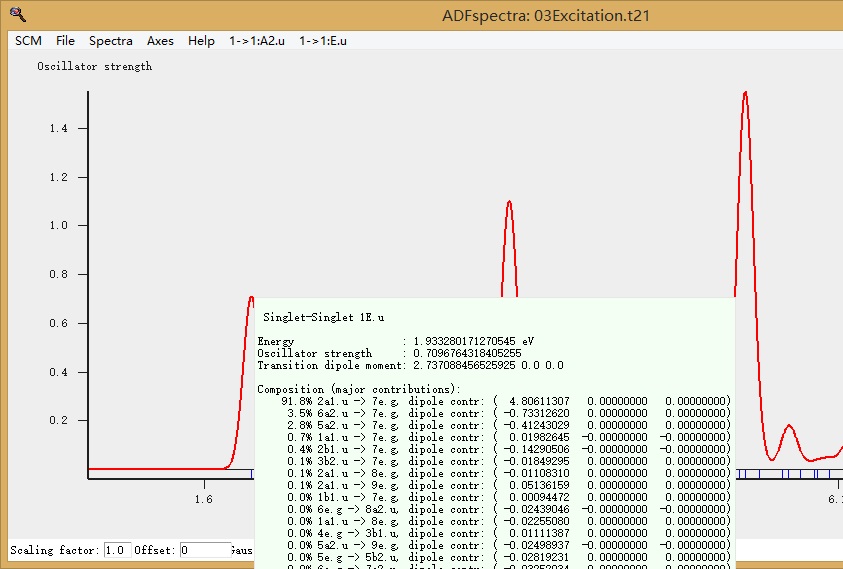
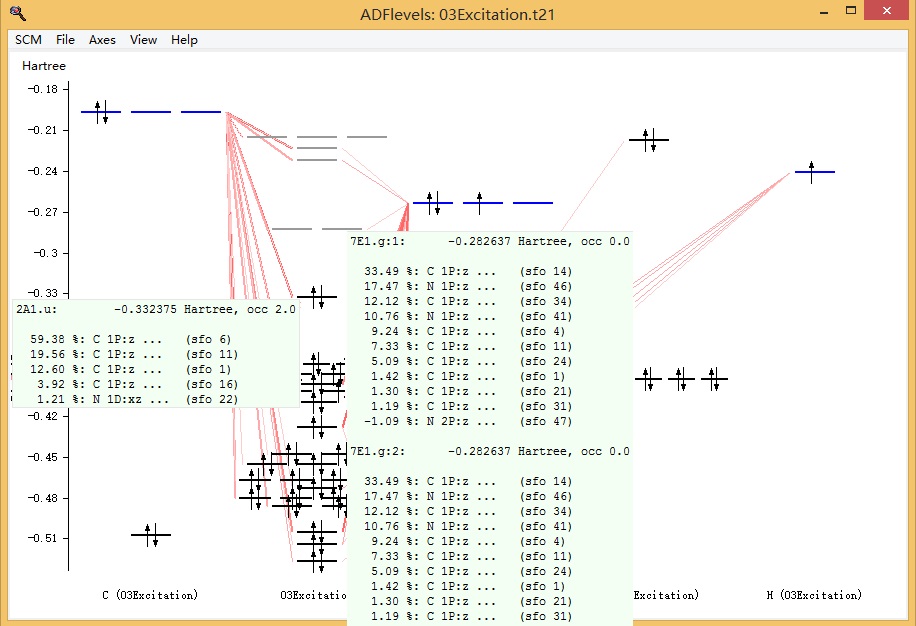
将鼠标置于吸收峰处,或者至于该吸收峰对应的横轴的细蓝线处,即显示该激发态或吸收峰的构成,例如下图:
为能量最低的激发态(S1),其构成为:91.8%从2a1.u激发到7e.g,即从a1.u不可约表示的第2个态激发到e.g这个不可约表示的第七个轨道,而这两个态,在SCM-levels中查看,实际上就是HOMO(最高占据轨道)和LUMO(最低空轨道),当鼠标移动到对应的能级上,即分别显示对应的轨道序号和组成:
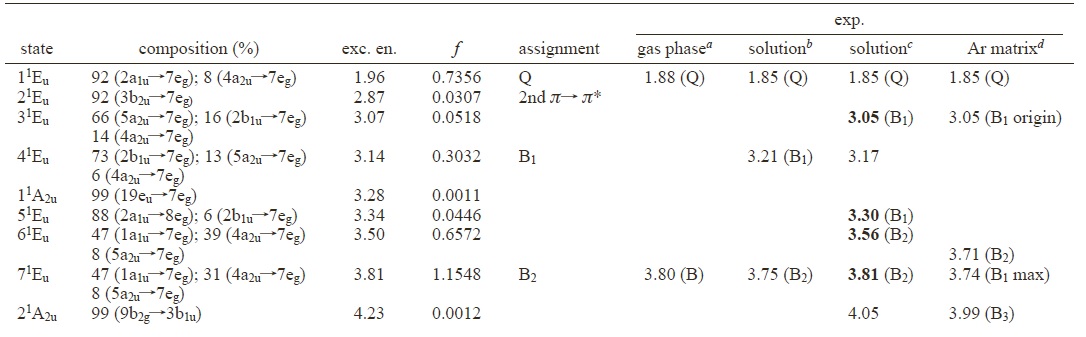
需要说明的是,e.g是二重简并的不可约表示,所以每个e.g能级其实都有两个轨道,能量相同(这两个能级假如要往上面填充电子的话,就可以填4个电子)。这在上图中,也可以看到。同时该激发态的振子强度为0.7097.振子强度与吸收强度成正比。则文献的列表中对应着f的那一列,例如对于S1态振子强度为0.7356。对应地,我们在文献中看到作者的计算结果中激发态的列表:
能量最低的激发态,也就是表中的第一个激发态。其中state列,列举的是激发态的名称,字母例如Eu表示激发的不可约表示,字母左上角的数字表示激发态的自旋多重度,字母前面的数字则是标记激发态在该不可约表示中的排序,数字为1表示该不可约表示的激发的最低激发态。
上表中第一个激发态,激发能最低,实际上就是S1态。构成中,有92%是从HOMO激发到LUMO,其他小的成分则略有差别。我们一般只关心主要组分。其他小组分可靠性并不高。
需要说明的是,我们没有使用冻芯近似,因此基态轨道的不可约表示中,轨道的排序与文献中略有不同,例如此例中,我们的5a2u对应着文献中的4a2u。这种对应关系,可以从levels中找出来,HOMO往下a2u轨道分别为6a2u、5a2u……而文献中HOMO往下,则分别为5a2u、4a2u……,对应关系即因此而找到。
以上是激发态的计算完毕。
需要说明的地方:
1)通常而言,激发能与基态计算得到的轨道能关系很大,激发能实际上可以认为由两项构成:
第一项,即占据轨道和空轨道之间的能级差。拿此例S1态来说,也就是HOMO和LUMO能级之差。这一项往往占激发能的大部分,甚至达到90%。因此很多时候,我们用HOMO、LUMO能级直接来估算最低吸收峰。但也需要注意,有的时候,例如HOMO-LUMO为禁阻跃迁,那么最低激发就不是HOMO-LUMO激发,这种估算也就无效。
第二项,可以认为是占据轨道和空轨道之间的“耦合作用”,这种耦合作用大部分情况下很弱,但有时候很强,轨道的对称性对这种耦合影响很大。当耦合项很大的时候,前面提到的估算吸收峰的方式就不可靠了。
有的时候一个激发态的主要组分是好几个跃迁,这个时候,这种估算方式就更加无效了。
2)基于前面的原因,不同的泛函对激发能的影响也就非常大。因为不同的泛函计算得到的能级差往往差别很大。一般性地说,LDA计算得到的能级差最小,其次是PBE等,再次是B3LYP等杂化泛函或者SAOP。另外,冻芯与否,对能级也有较大的影响,但对能级差的影响次之。因此,一般而言,在激发态的计算时,取消冻芯近似(即:使用全电子基组)是恰当的。
3)激发态的质量:一般而言,例如B3LYP对于有机体系的低激发态,可靠性往往都是不错的,但更高的激发态,可靠性则会变差,越高的激发态,可靠性越差。其主要原因,往往也在于DFT方法本身,对于较高的空轨道能量、较内层的占据轨道能量的计算,效果都比较差。越是离HOMO-LUMO远的轨道,能量差的越多。更深层次的原因则是:DFT原则上,只有HOMO、LUMO的能级与真实的IP、EA有对应关系,而其他能级实际上与电子能级并没有对应关系;我们把DFT能级当作电子能级来使用,实际上是一种很粗糙的近似。
4, 激发态的结构优化:
如果我们需要计算荧光或者磷光,激发态的结构优化就是必须要做的事情。一般而言,激发态的几何结构和基态的几何结构不一定具有相同的对称性。因此分子处于激发态的时候,其对称性我们是不清楚的。因此,对于激发态的优化,我们应该将分子的对称性取消掉,然后进行优化。优化之后,如果保持了原有的对称性结构,那就可以认为激发态对称性与基态一样(这种情况其实很少见);如果优化后,对称性消失了,或者降低了,那就只能认为激发态的对称性消失或降低了(大部分情况是如此);也有对称性变高的情况,但非常少。
ADF计算的精确度很高,因此能够让结构收敛到正确的对称性上面去。例如CO2分子,我们从一个对称性最低的结构,例如Cs群的结构去优化,最后收敛后,ADF也能得到D∞h的直线型结构。
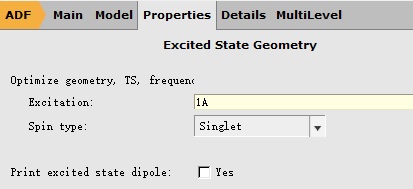
由于我们取消了对称性,因此激发态的不可约表示就变成一个A了。最低激发态,也就变成1A了。因此我们如下设置激发态优化的参数(分子结构沿用上一步的结构):
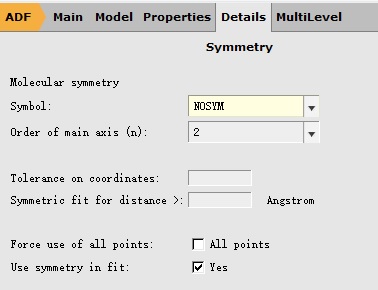
同时取消对称性如下:在Details下拉菜单中选择Symmetry得到如下菜单:
保存任务,例如名为:04Excitation_GO,则自动生成04Excitation_GO.adf、04Excitation_GO.run文件。同时会生成04Excitation_GO.pid文件,这个文件对我们一般没有用处。然后执行任务。
5, 结果分析
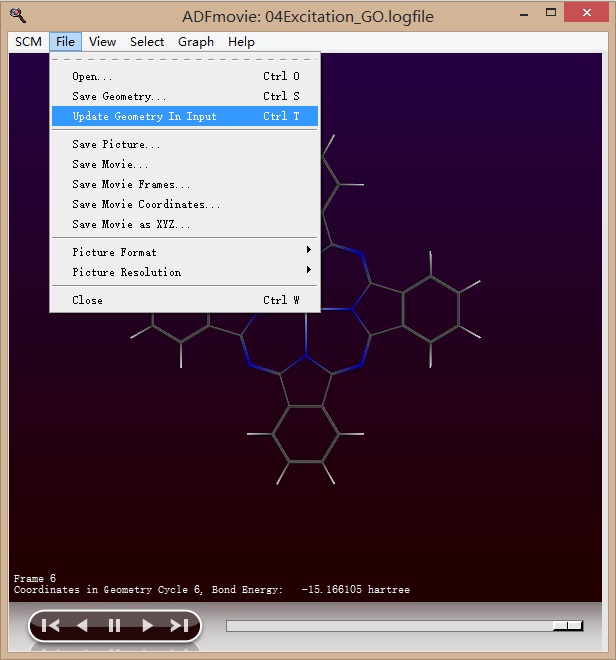
优化后的分子结构,可以从SCM-movie中播放的优化过程动画的最后一帧看到。导出该结构可以用如下方式:
也可以选择Save Geometry将其保存为xyz格式。而优化结束之后的激发态,与前面一样,可以在SCM-Spectra中查看。可以看到新的S1态的激发能。这其实就对应着荧光的发射峰。组分等也可以同样查看到。这部分工作该文献中没有进行,包括下面的激发态频率计算,文献中也没有做。
6, 激发态频率计算:
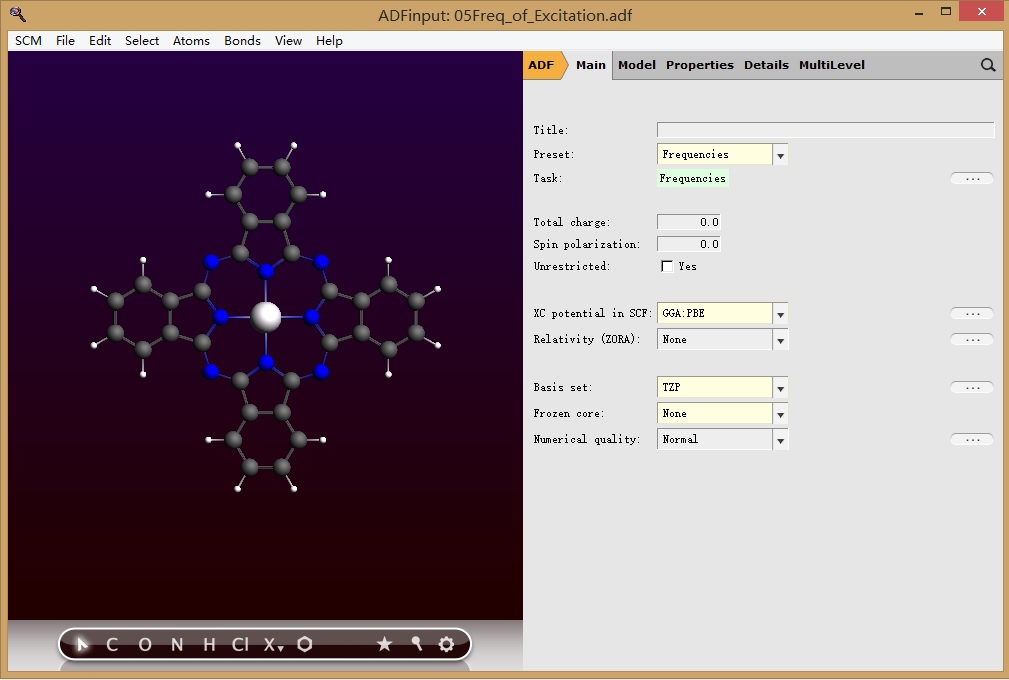
本步计算的分子结构是上一步计算得到的结构。可以从movie中File-update Geometry In Input得到,也可以从File-Save Geometry得到的xyz文件导入。参数设置(这一步需要非常小心,否则会变成基态的频率计算)如下:
保存任务,例如名为05Freq_of_Excitation。运行计算。
注意:
激发态频率的计算,实际上是使用数值拟合的方式去计算。也即是说,需要将每个原子逐个从平衡位置做微小偏移动,然后计算这种微小形变之后的激发能,因此对于像这样的大分子,计算激发态频率将是非常耗时的。如果不考虑对称性的话,计算的结构数大约为原子个数的6倍——也即是说需要计算这么多次激发态。ADF激发态的并行效率很高。因此高核数并行对于这样的计算很重要,否则几乎不可能完成这样的计算任务。总体而言ADF的效率不错,本计算在4核台式机上完成,大约用了4天。如果在16核服务器,基本上1天就足够了。
7, 结果查看:
同样地,在SCM-Spectra中可以查看到振动谱:
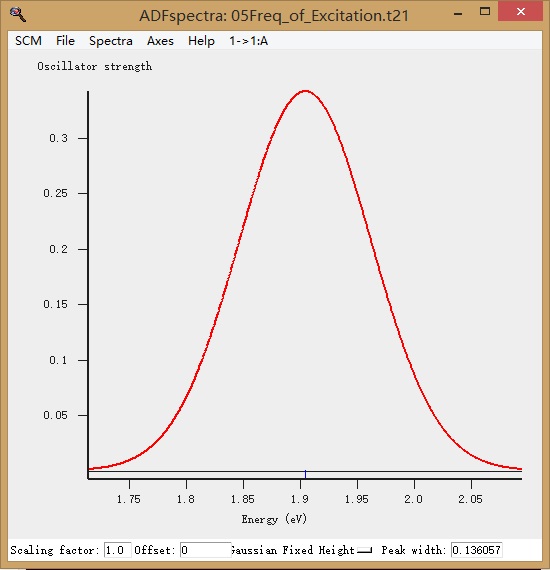
首先显示的是激发态(我们上面只计算了1A这一个激发态,因此只有一个峰):
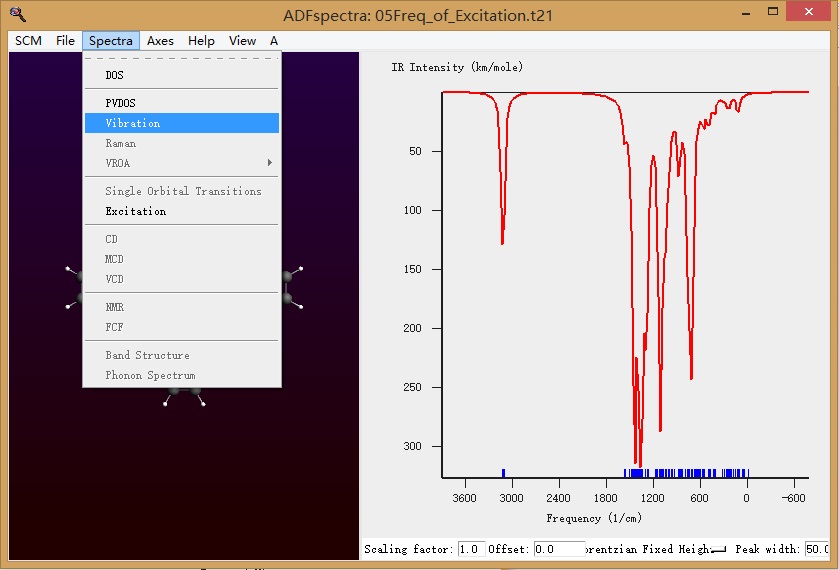
选择振动谱:
即得到右方的振动谱。振动谱中没有虚频(负数的频率)。
8, 如果计算振动分辨的电子光谱:
需要利用激发态的振动数据以及基态的振动数据。在ADF中,使用FCF程序可以进行这样的计算。制作一个后缀为.run的文本文件,内容如下:
$ADFBIN/fcf << eor
STATES 02GS_Freq.t21 05Freq_of_Excitation.t21
QUANTA 3 0
TRANSLATE
ROTATE
SPECTRUM 0e3 20e3 1001
eor
需要注意的是第二行和第三行:
其中第二行是02GS_Freq.t21和05Freq_of_Excitation.t21分别是基态频率计算(此处没有进行额外讲解,具体可以参见ADF的GUI Tutorial;该文件则ADF2014.01/doc/PDF/文件夹下;该文件夹内还有其他手册、文档)、激发态频率计算产生的*.t21文件。在Linux中,如果这两个*.t21文件与此*.run文件在同一个目录下面,则不需要指明路径,如果不在同一目录下,则需要分别指明两个*.t21文件的路径。在window下计算,一定需要指明文件的路径。例如:
STATES F:\ADF_Case\03Fluorence02GS_Freq.t21 F:\ADF_Case\05Freq_of_Excitation.t21
第三行是用于指出上面的两个振动的振动量子数。例如此例中QUANTA 3 0,表示计算S0态的前三个振动态(各个振动模式的振动基态、第一激发态、第二激发态、第三激发态)与S1态的振动能量最低的振动模式的振动基态之间的Franck-Condon因子。如果是QUANTA 0 0则表示计算S0态的振动能量最低的振动模式的振动基态与S1态的振动能量最低的振动模式的振动基态之间的Franck-Condon因子。
TRANSLATE与ROTATE分别表示将平动和转动考虑在内计算振动模式之间的“跃迁”, SPECTRUM 0e3 20e3 1001表示计算跃迁能量为0到20000波数之间的1001个点的“跃迁”强度。
即可运行。在生成*.out文件可以查看结果。其中
Ground state to ground state overlap integral: 0.7427127782
Number of Franck-Condon factors calculated: 13861
Avg. sum of Franck-Condon factors for the first state: 0.8893560618
Avg. Sum of Franck-Condon factors for the second state: 0.6416247470E-04
这部分两个态(我们此处命名为a和b)的关系:avg(a)N(b)=avg(b)N(a)
振动分辨的电子光谱的计算,需要参考其他文献,此处不详细展开。