概述
众多可持续发展目标需要探索和生产新的可持续材料。作为最有前途的材料之一,多孔金属结构由于其较高的表面积、刚度和孔隙体积及固定的孔隙网络成为改善流体和传热的理想候选材料。固体含量较高的泡沫为闭孔金属泡沫,而固体含量较低的泡沫为多孔金属泡沫。材料的拓扑和孔隙结构特征往往受到生产工艺(发泡、铸造、烧结等)路线和操作条件的影响,可由几乎所有液态金属或金属粉末制成,包括铝、铜、镍、钢、铁和合金。多孔金属可广泛应用于航空航天、热力水力输送、燃料电池、吸声板、空气净化技术和环境减排等。
为设计可应用于高效传热传质的金属泡沫,了解其流体结构特性、流体流动状态和边界是非常必要的。本项目采用多学科方法,利用实验、计算流体动力学(CFD)建模和仿真以及人工神经网络(ANN)机器学习反向传播研究液态熔体渗透技术制备铝泡沫的流体动力学。
图像处理
将含 99% 铝的液态熔体加热至 800 ℃ 后分别倒入由近球形盐、软水盐和粒状盐的空心填充床组成的模具中,凝固后压实。
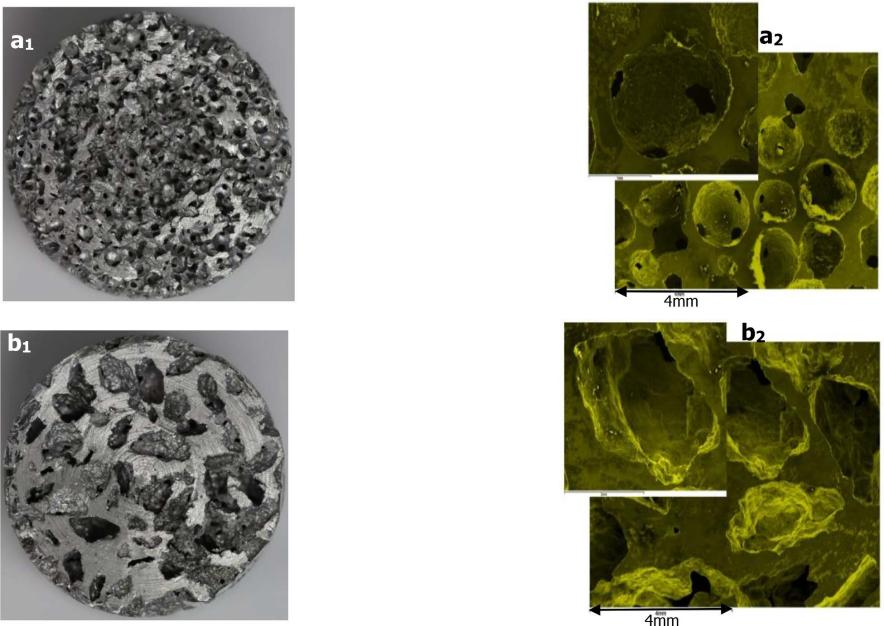
使用 Zeiss Xradia Versa XRM-500 X 射线计算机断层扫描(CT)系统获得图像数据集(3000 张 TIFF 格式),导入 Simpleware 软件中进行图像处理,应用各种工具(阈值、滤波器、腐蚀和膨胀等)生成 3D 体积结构。在Simpleware ScanIP 模块中,从一个大的 3D 模型中裁剪出合适的 3D RVE(代表性体积单元)结构,使其测量的孔隙率与实验得到的名义孔隙率仅相差 ±3 %,尺寸为材料平均开孔直径的 3-5 倍。在 ScanIP 中可以直接测量铝泡沫的孔隙率、体积和表面积,平均孔径和平均开孔通过平均分水岭分割孔隙和开孔流体域 3D RVE 的中心线得到。
在 Simpleware FE 模块生成 3D RVE 流体域的四面体网格模型,最小和最大边长分别为 3 倍和 7 倍体素尺寸,获得 5 种铝泡沫试样的最佳网格密度(2.6-3.1 Mcells)。设定边界条件,求解 Navier-Stokes 方程。

实验
本项目重复达西实验,构建恒水头渗透仪测量 18-20 ℃ 下流动液体/水通过多孔铝泡沫的渗透速度(vs)和水头损失(ΔH)。为避免流体损失并保持对流体通过泡沫结构孔隙和窗口的完全控制,设置管道系统内径与泡沫结构内径相同。将测量的水头损失(ΔH,mmH20)转换为压降(ΔP,Pa),拟合压力/速度到方程确定多孔结构的渗透率和形状阻力特性。单位压降 ΔP/L 可表示为:
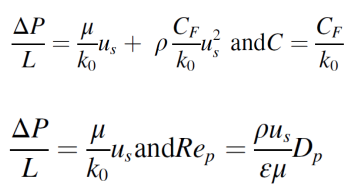
其中,k0 是渗透率,CF 是 Forchheimer 系数,µ 是流体动力粘度,ρ 流体密度,us 是表层流体速度,C 是形状阻力,ε 和 Dp 是材料孔隙率和平均孔径。
结果和讨论
铝泡沫试样 A-E 的孔隙结构相关和流动信息如下所示,由公式计算泡沫的渗透率和惯性(Forchheimer)系数。通过将液态熔体渗透到由近球形盐床形成的收敛间隙而制成的泡沫 C 渗透率最低(1.291 × 10-09 m2),具有最宽平均开口孔隙(0.212 mm)的泡沫 D 渗透率最高(8.479 × 10-09 m2)。处理泡沫 A-D 的渗透压力(0.5 bar)相似,但由于盐颗粒形状和尺寸的差异,它们的平均孔径显著不同。根据经验,泡沫 E 应比泡沫 D 具有更宽的平均孔径,但前者在 1.0 bar 的较高压力下制成,影响了孔径的尺寸。与其他研究结果一致,多孔金属泡沫的孔隙率和惯性系数之间呈指数反比关系。
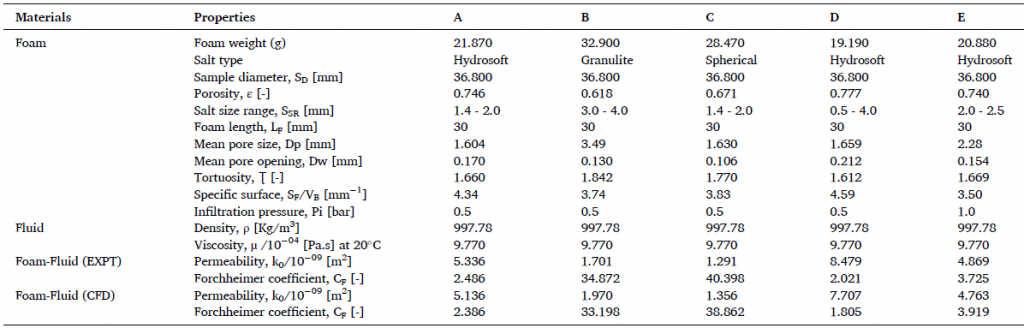
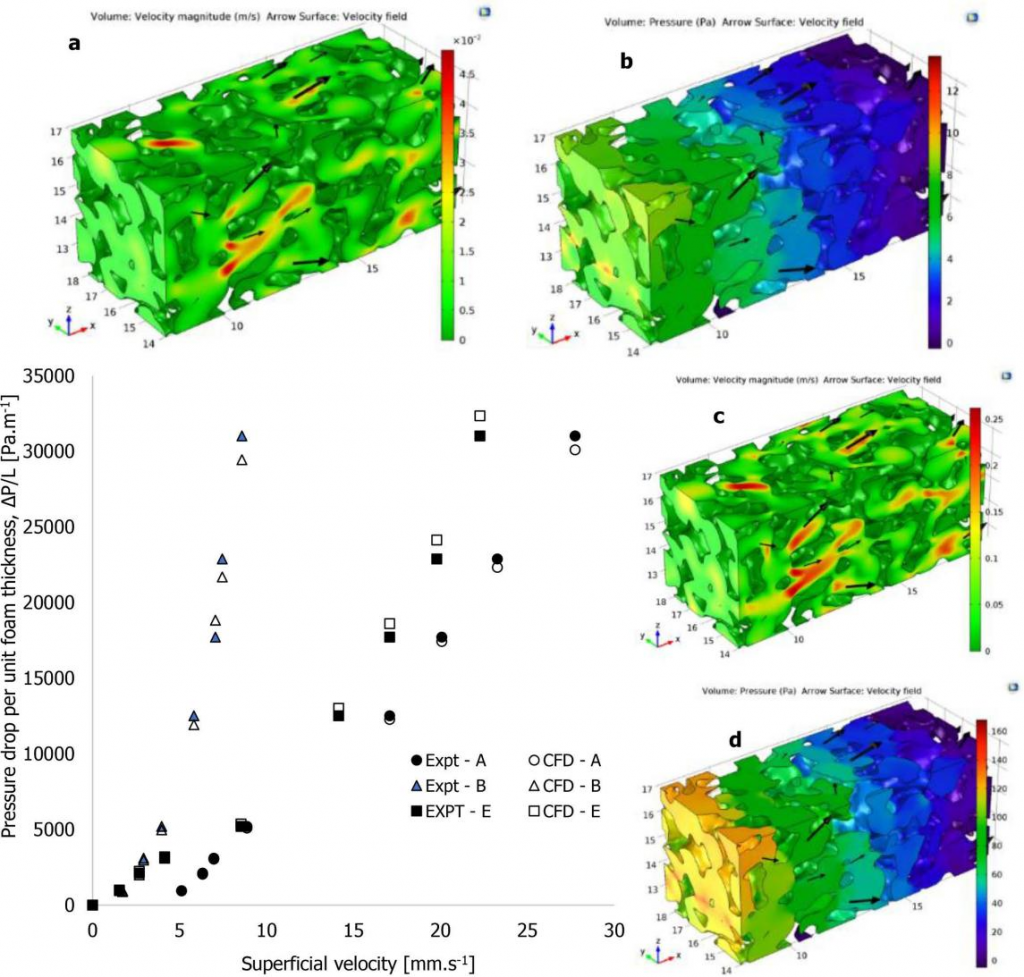
五种泡沫铝的单位压降与表层水流入速度关系图显示出多孔材料典型的压力和速度之间的二次函数关系,具有近乎完美的相关系数(R2 ~ 1.0)。对于孔径较大和孔隙率较高的材料,流量限制较小。而对于孔径较小和孔隙率较低的材料,流量限制最高。
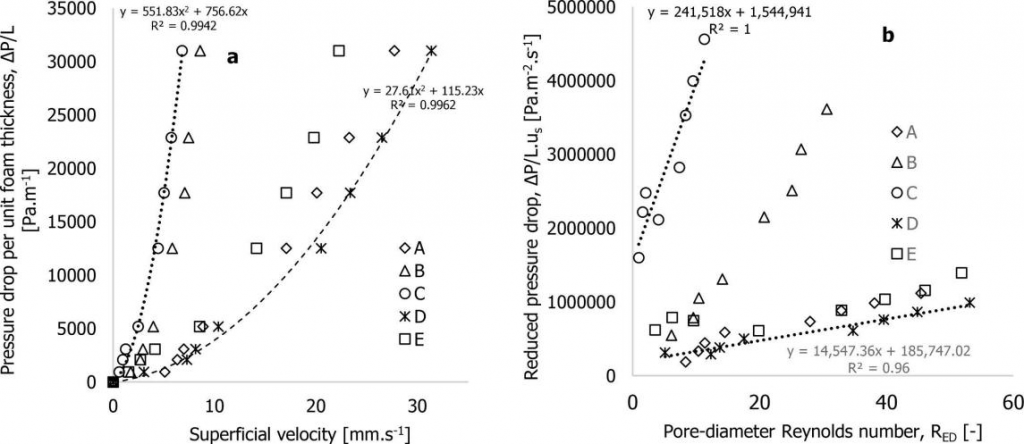
降低压降与无量纲孔径雷诺系数的关系用于描述流动流体状态。泡沫 C 的孔径雷诺数(Rep)范围在 0.99 至 11.32 之间,具有更宽平均孔径和孔体积分数的泡沫 E 范围在 5.13 至 53.15。将多孔介质的流态分为达西流态、前 Forchheimer 流态、Forchheimer 流态、后 Forchheimer 流态和湍流流态。基于孔径雷诺数在 0 到 1 之间对应达西流态,1 到 10 代表前 Forchheimer 流态(即从达西流到惯性流),完全发展的惯性流在 10 到 150 之间,湍流则高于 300。
粘性流在多孔介质中占主导地位,其流动渗透率受到拓扑结构的强烈影响。在 Forchheimer 流体流动状态下,降低的压降与表层入口流体流速线性相关。边界层开始在孔壁附近形成,从而产生依赖于孔体积分数(孔隙率)和比表面积的惯性力。当流体通过连续的隔室、开口孔隙和狭窄韧带时,动能在运动的流体和孔壁之间耗散,因此在这种情况下的流动速度很高。
CFD 预测数据与泡沫 A 实验数据的差异(2.3%)几乎可以忽略不计,泡沫 E 的差异最为显著(4.3%),表明相对较小的 3D RVE 样本(3-5 倍平均开口孔隙)足以对流动信息进行相对准确的预测。下图展示了流体如何从左向右流动,强度随入口流向出口而降低。观察结果表明,泡沫结构的开口孔隙内强度较高。泡沫 C 的强度最高,其平均开口孔隙最窄(0.106 mm);而泡沫 A 的强度最低,其平均开口孔隙最宽(0.172 mm)。因此,泡沫流体特性由材料中开口孔隙以及其他孔结构相关特性驱动。
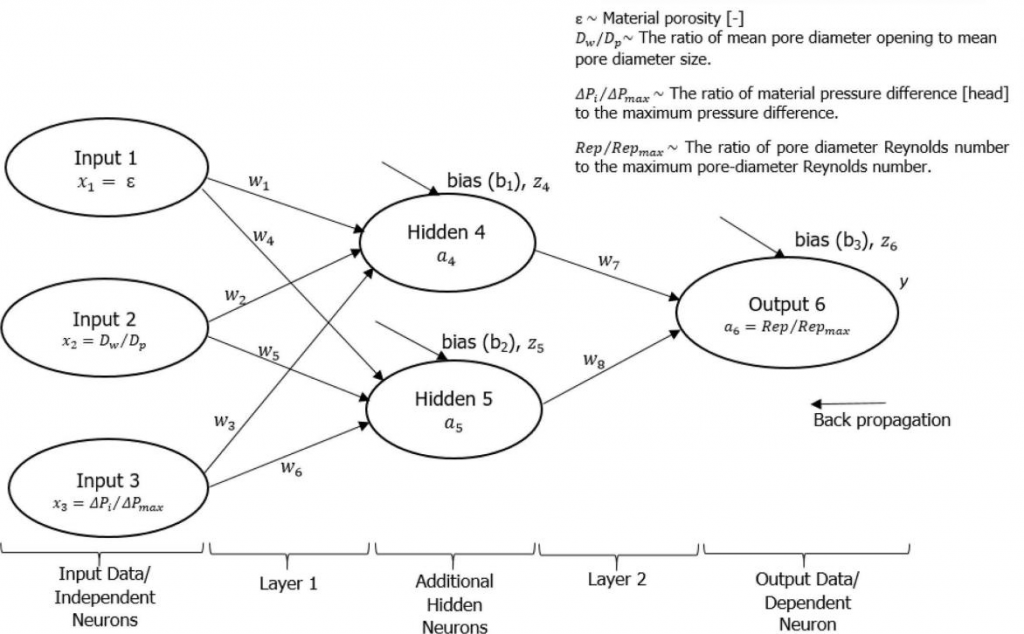
反向传播人工神经网络分析实验数据
为预测实验输出,任何人工神经网络(ANN)都需要与具有突触权重(wi)和偏差(bi)的多个输入(xi)和输出(y)信号进行交互。ANN 模型中将孔径雷诺数与最大孔径雷诺数(53.16)的比值作为预测输出信号(a6),所有输入信号(x1、x2 和 x3)均设置为从 0 到 1。由于实验输出和输入信号不是线性的,因此建议使用隐藏节点(神经元)。卷积和非线性可以通过添加更多隐藏层(即简单地添加更多神经元)来改进。关键目标是通过简单地训练 ANN 模型设置,在无论是否存在额外隐藏神经元(深度神经网络 DNN,单神经网络 SNN)时改进预测输出信号,使其与实验测量值紧密匹配。
调整线性率,将成本函数降低至接近于零,这对于得出结论至关重要。在 ANN 网络的训练过程中,在初始和中间或中间和最终任意值之间获得数值,最终训练数据的成本为 0.9648。ANN 模型产生的输出信号是恒定的(0.94),但与实验结果(Rep/Repmax)有显著偏差。然而,随着 ANN 网络继续训练,通过系统处理连续学习,预测值将越来越接近实验值,从而获得更好的输出信号。
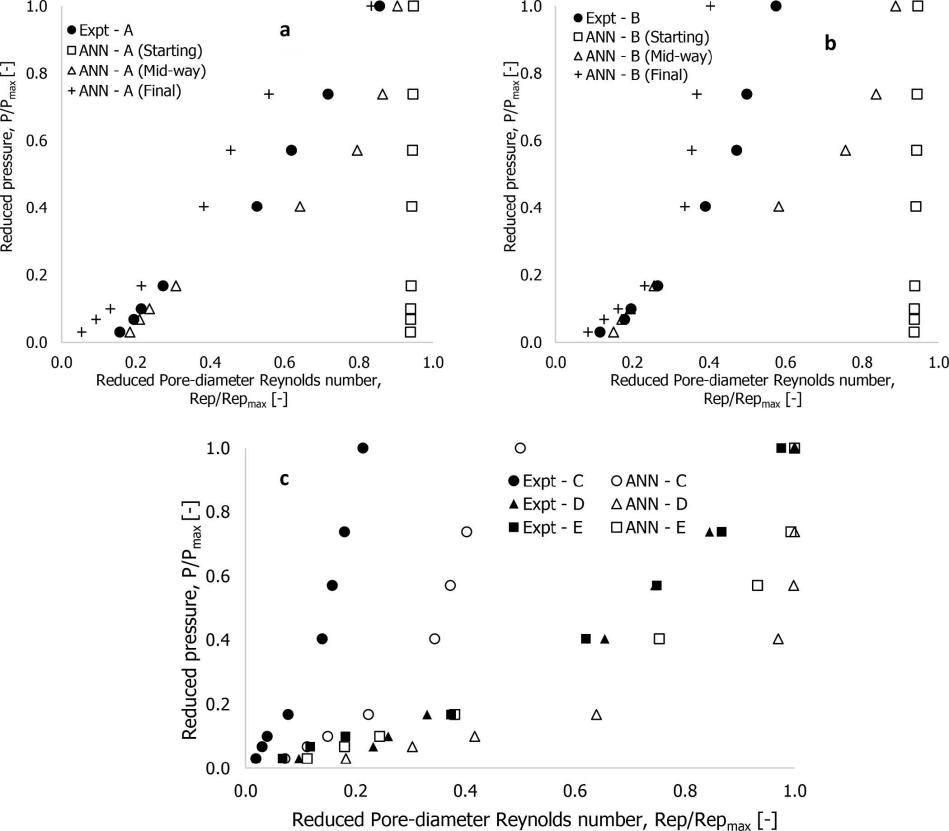

对于所有泡沫结构(A-E)使用最终值时,实验和 ANN 预测的输出信号之间偏差都很大。因此,在 ANN 模型的隐藏层中添加神经元以改进输出信号。
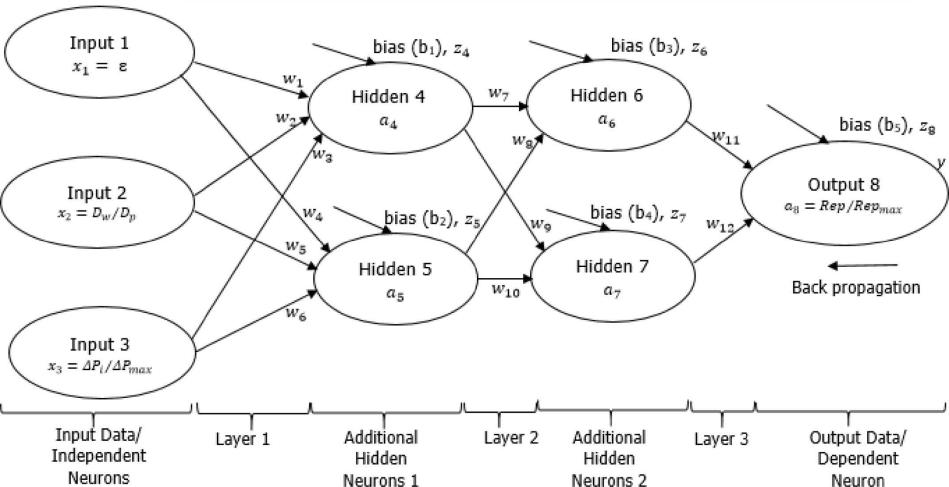
双层 ANN 模型的实验测量值和预测值间的偏差通常在 2%- 50%,而使用三层 ANN 模型获得的最终输出信号在 0.3%-9%。
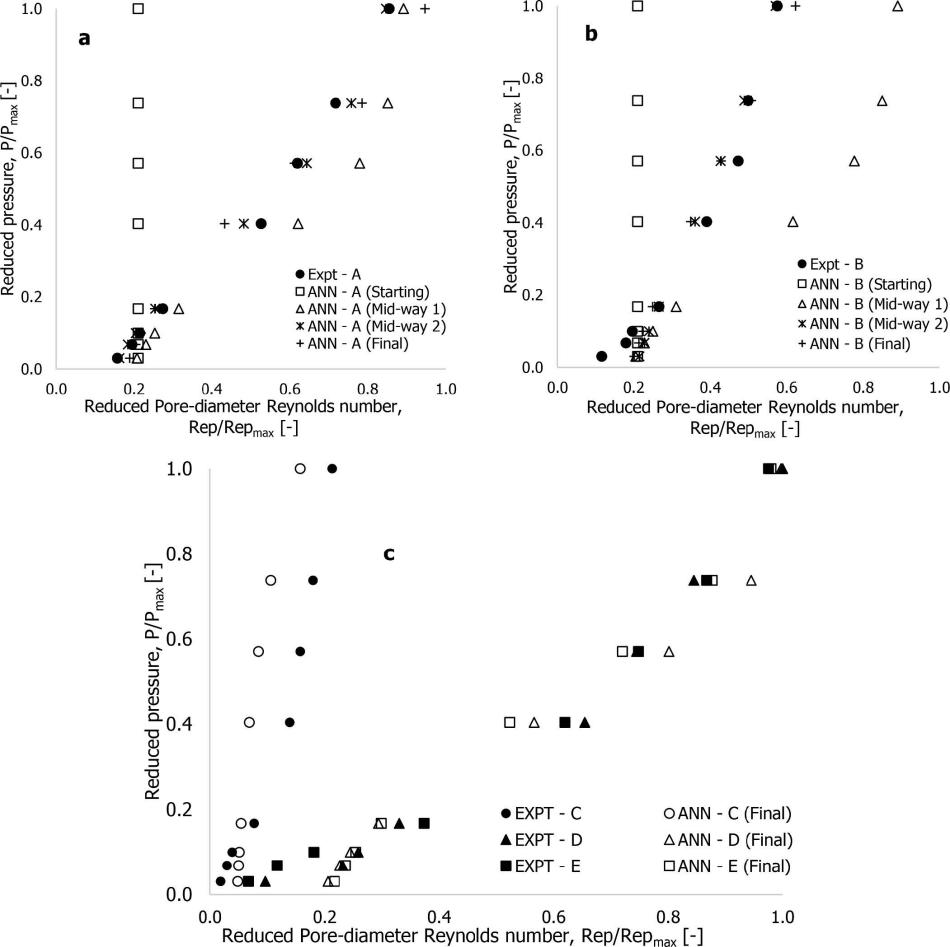
三层 ANN 模型在网络训练停止并获取值之前,使用 0.01 的线性率,成本降至 0.152。如果在更长的时间内进一步训练,最终值可能会更接近于零。最终训练的突触权重w2(4.673)远高于权重w1(-19.892)和w3(0.669),表明多孔材料开口孔径变化(输入2)极大地影响着隐藏输出 4。而材料孔隙率(输入 1)对隐藏输出 5 的贡献更高,但隐藏输出 4 对结构粘性状态(渗透率)的贡献比输出 5 更大。这些发现证实了金属泡沫的孔隙率和开口孔径对于获得最佳流体流动性能至关重要。

结论
在本研究中,通过液态熔体渗透到盐填充床形成的收敛间隙制成多孔铝泡沫,使用 X 射线计算机断层扫描数据对试样的多孔结构进行表征和三维高级图像分析。对具有不同孔径、开口孔隙和间隙的多孔金属泡沫进行实验和计算流体动力学模拟,使用恒水头渗透仪技术提供流体流动信息。虽然渗透率和 Forchheimer 系数都取决于孔隙结构相关特性,但前者在低速时占主导地位,后者在高速时占主导。CFD 模拟与实验结果相当一致,表明开口孔隙对泡沫间隙内的流体流动状态有显著影响,进一步证实了孔隙尺度技术为此类复杂材料提供有用信息的可行性。
使用机器学习反向传播人工神经网络建立孔隙结构相关特性和流体流动信息之间的关系。通过隐藏神经元网络关联输入和输出信号,改善数据的卷积和非线性。在对 ANN 模型进行后续训练后,预测处于实验分散范围内(偏差在 0.3%-9%),三层 ANN 模型比双层模型能更好地预测结果。泡沫的孔径和孔隙率被认为是影响流体流动特性的因素,且被发现会影响泡沫流体动力学的渗透性(粘性主导)和 Forchheimer 系数(惯性主导)。基于这种方法,隐藏神经元的添加可以改进预测输出信号并减少训练时间,从而改善金属泡沫材料的输出信号。
参考文献
- Otaru A J, Alhulaybi Z A, Owoseni T A. On the hydrodynamics of macroporous structures: Experimental, CFD and artificial neural network analysis[J]. Chemical Engineering Journal Advances, 2023, 16: 100545.
