复数能带的概念和求解方法
对于周期性固体,薛定谔方程 Hψnk=EnkSψnk (S为重叠矩阵)中的 ψnk 可以写为 ψnk(r)=e−ik⋅rUnk(r),这里的 Unk(r) 是与晶体自身周期性相同的周期函数。在一般的能带结构计算中,给定一系列实数的波矢k(通常位于第一布里渊区的高对称方向上) ,可以通过求解上面的薛定谔方程得到不同 k 值上的本征矢,由此确定本征能量 Enk (即能带结构)。
在给定能量 E时,可以求解满足薛定谔方程的 k 值。这种解法可以得到实数和复数的 k,实数 k 的解是通常的 Bloch 态,而带有虚部的解是在一个方向上呈指数递减,相反方向上递增。这样的解通常不能稳定存在于块体材料中,因此在能带结构计算中通常被忽略。然而,它们可以存在于表面或界面处,并且可以提供关于电子态如何在材料中衰减的信息。计算复数能带的方法可参考:
- Yia-Chung Chang and J. N. Schulman. Complex band structures of crystalline solids: An eigenvalue method. Phys. Rev. B, 25:3975–3986, Mar 1982. doi:10.1103/PhysRevB.25.3975。
复数能带与衰减电子态
下图清楚的显示了复数能带上不同点的波函数形态:实数能带具有完整的周期性,而复数能带则呈现衰减态。
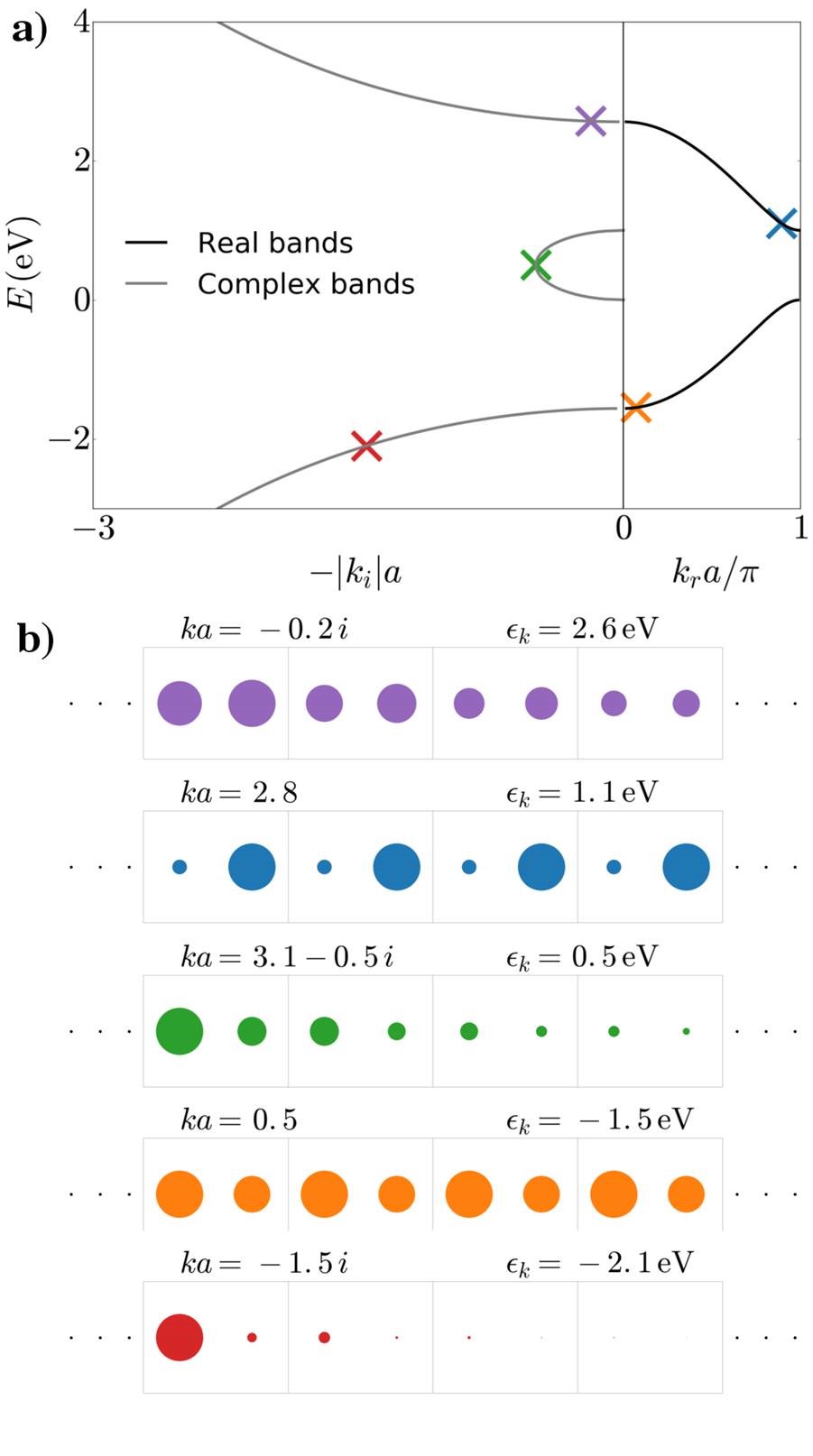
复数能带与电子透射
对于导电结,很自然地可以通过材料的电导-长度依赖性β来表征材料,此依赖性可以通过计算复数能带获得。更多关于复数能带结构的概念和在导电结中的应用,请参考:
- Jensen, A. et al. Complex band structure and electronic transmission eigenchannels. J. Chem. Phys. 147, 224104 (2017)。
作者利用复带结构和DFT-NEGF-LANDAUER输运两种基本理论都可以对β进行理论估计复数布洛赫波和传输本征通道都揭示了单个态β的信息。作者给出了由复带结构确定两种最导电状态的衰减常数的计算,以及分子结和半导体结的标准DFT-NEGF输运计算。结果表明,尽管这两种方法的性质不同,但分子结的衰变常数计算值有很强的一致性,而半导体结的衰变常数计算结果存在一定的差异。
下图显示电子态如何隧穿通过不同厚度的势垒。
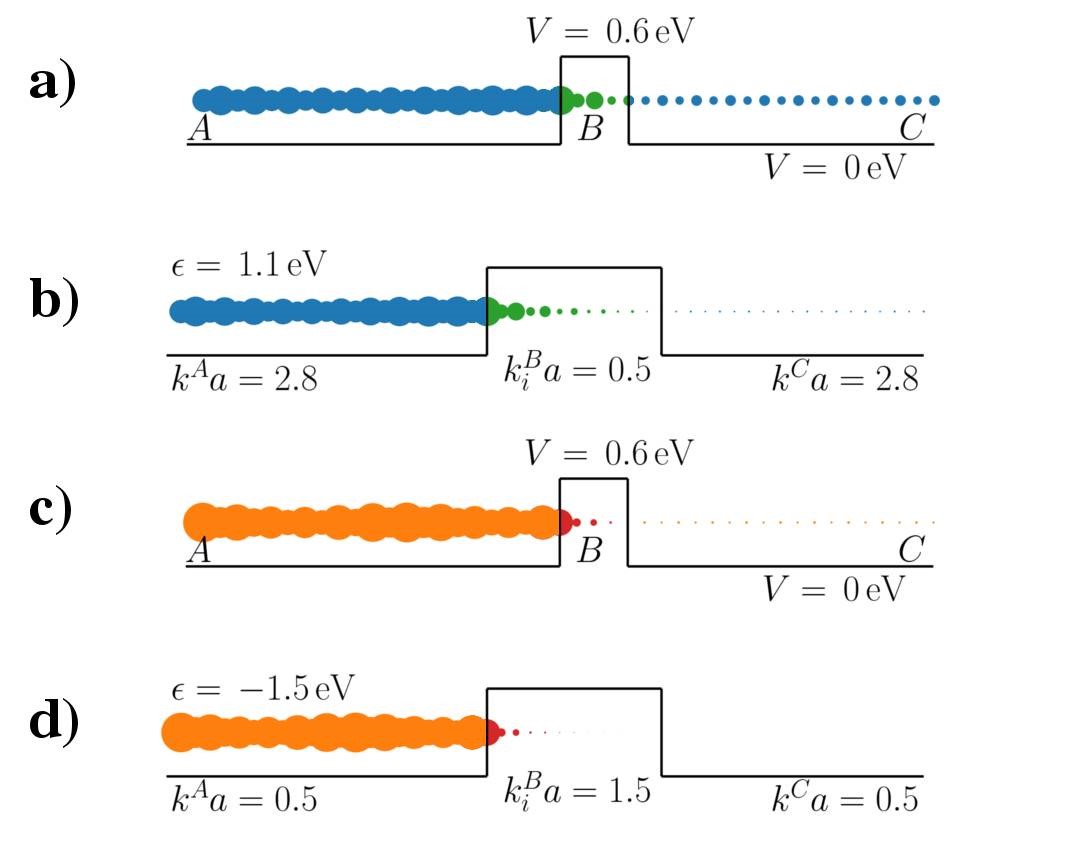
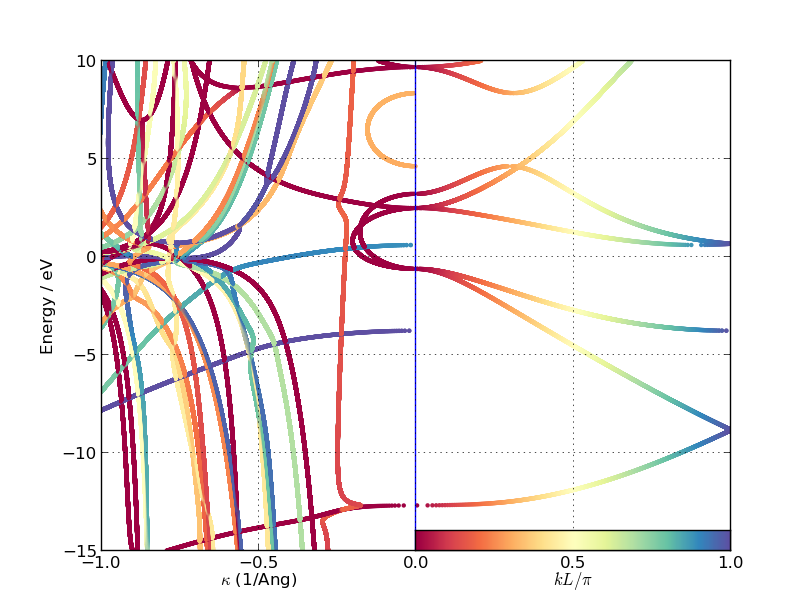
计算实例
立即试用 QuantumATK!
