基于 µCT 建模研究亚麻纤维的形态和力学性能

概述

在当前可持续资源需求持续增长的背景下，植物纤维作为玻璃纤维等合成纤维的替代材料，近年来在市场上的能见度与占有率逐渐提升。在各类植物纤维中，亚麻纤维相较于玻璃纤维因其已通过生命周期评估证实的环境优势而备受关注。但在结构产品中的大规模应用仍受到多重因素的制约，植物纤维的自然特性在不同层面上引入了变异性，给更好地理解结构-力学性能关系带来了巨大挑战。

本研究基于 µCT 扫描图像数据创建亚麻纤维的微观结构模型，采用有限元方法模拟复杂纤维形态引起的局部应力和应变分布，探索形态特征对力学性能的影响。

图像处理和模拟

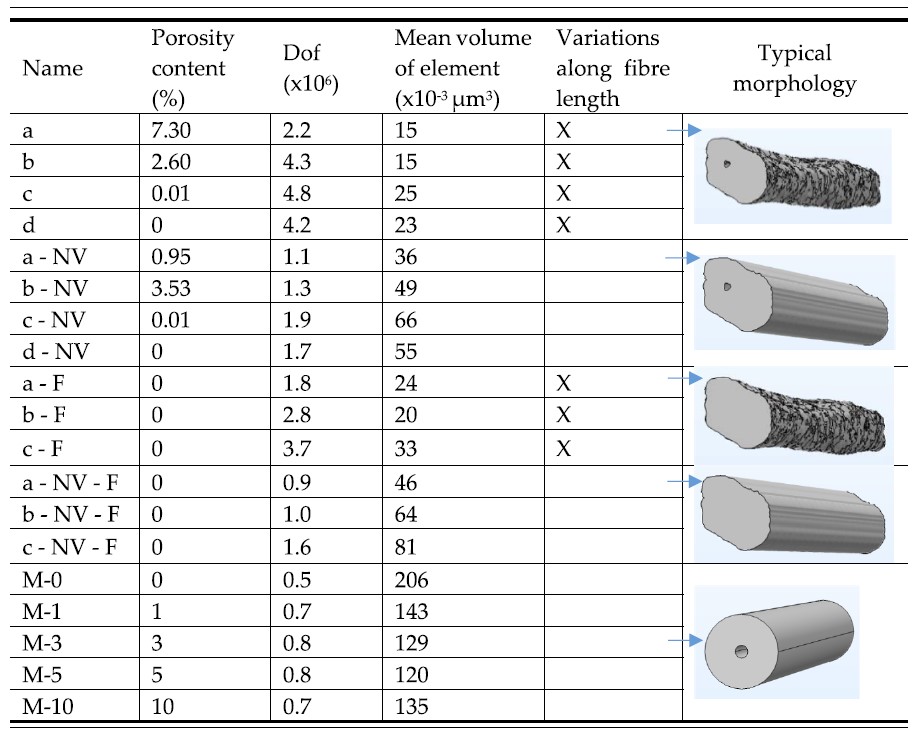
遵循标准 NF t 25-501 对 42 根单元纤维进行拉伸测试实验。使用 Zeiss Xradia 510 versa 设备进行扫描，获得 4 个单一亚麻纤维（a-d）的图像数据，体素尺寸为 150 nm。将 μCT 扫描图像数据导入 Simpleware 软件进行图像处理，由于亚麻纤维中不同亚层的 X 射线吸收特性相近且外部层状结构厚度极薄，无法通过 X 射线显微 CT 实现亚层区分。因此，在分析中将纤维简化为仅由形成较厚细胞壁的胶质层（G 层）构成。为进行对比，取纤维一端的横截面沿长度方向延伸（横截面无变化）记为 -NV；使用工具填充内部孔隙后的纤维分别记为 -F 和 -NV-F；构建直径为 15 μm 的圆柱形理想纤维（内腔占比为 1-10 %）记为 M。

在 Simpleware FE 模块生成高质量的四面体网格模型，为寻求计算时间和结果精度间的最佳平衡进行了收敛性测试。调整纤维 a 的网格粗糙度和体素尺寸，使自由度数量为 1.1 × 10⁵ 至6.3 × 10⁶，平均单元体积为 5 × 10³ 至 325 × 10³ µm³。通过整体刚度误差和应力分布曲线评估模拟结果的准确性。为精确表征纤维的孔隙率进而计算杨氏模量，同时保证具有足够的分辨率捕捉表面粗糙度和内腔复杂形状引起的应力集中，所有纤维均采用所测试的第三种网格粗糙度，模型尺寸的自由度介于 9 × 10⁵ 至 5 × 10⁶。

长度为 140 μm 至 10 mm 的纤维在拉伸测试实验中预测杨氏模量的差异可以忽略不计，通过改变无内腔纤维的长度（50 μm 至 10 mm）评估相同边界条件下不同纤维长度对杨氏模量的影响。结果显示边界条件引起的应力集中对总纤维长度的影响小于 10 %，统一选取纤维长度为 140 μm。

将体积网格模型导入 COMSOL 软件进行求解，假设材料为线弹性，忽略粘性和塑性行为。在纤维素微纤丝关联的坐标系中，纤维细胞壁可视为横观各向同性材料，其对称轴沿微纤丝取向排列。

结果与讨论

形态

对四根纤维的几何形态及内腔进行三维体积量化分析，统计纤维横截面上纵横比、表面积、孔隙率沿纤维长度的变化。纤维 b 和 c 的纵横比沿长度方向相对稳定，平均值介于 1.04 至 1.26。纤维 a 和 d 的纵横比和标准偏差较大，表明沿长度方向的形变。

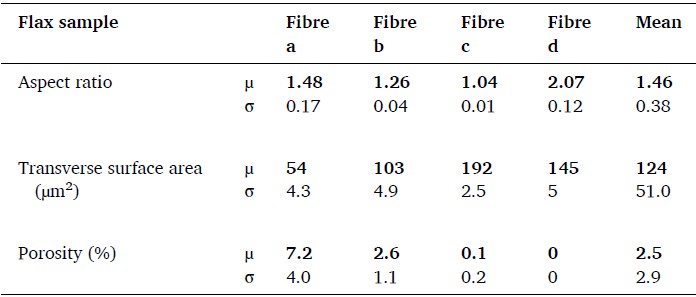
纤维间的孔隙率存在较大差异，平均孔隙率为 0-7.2 %。纤维 a 和 b 在部分区域孔隙率接近 0，表明这些部位的内腔发生狭窄化。内腔的某些区域可能受限于 150 nm 体素分辨率，纤维 c 中几乎无法识别内腔结构，仅在特定位置出现约 2% 的孔隙率，可能源于缺陷的形成。未检测到纤维 d 的内腔，推测是前期纤维变形所致。

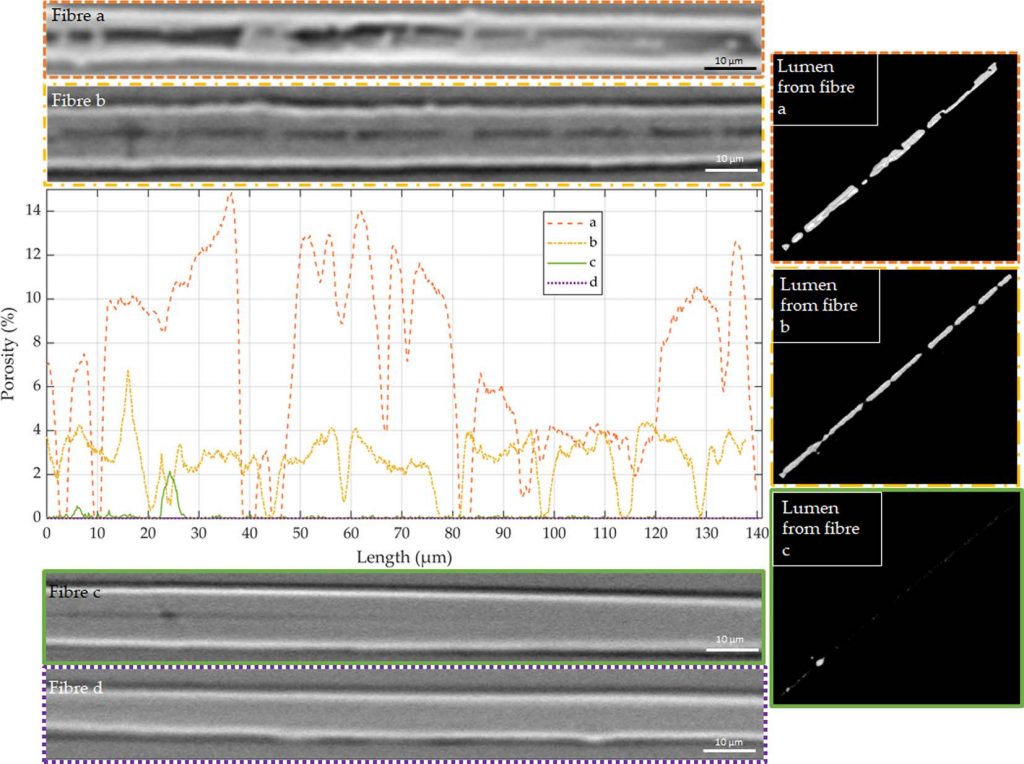
总体预测行为

对纤维施加 1% 的变形，方向 1 和 方向 2 的位移揭示了纤维几何形态（取向与截面变化）引起的非对称位移分布。基于线弹性假设，模型成功捕捉到了 μCT 观测到的纤维表面应力异质性。由于纤维具有屈服应力，持续增加的载荷导致模型中应力被高估，但仍能反映出由表面粗糙度引起的应力集中。与之相反，圆柱形纤维的应力分布则呈现均质特性。

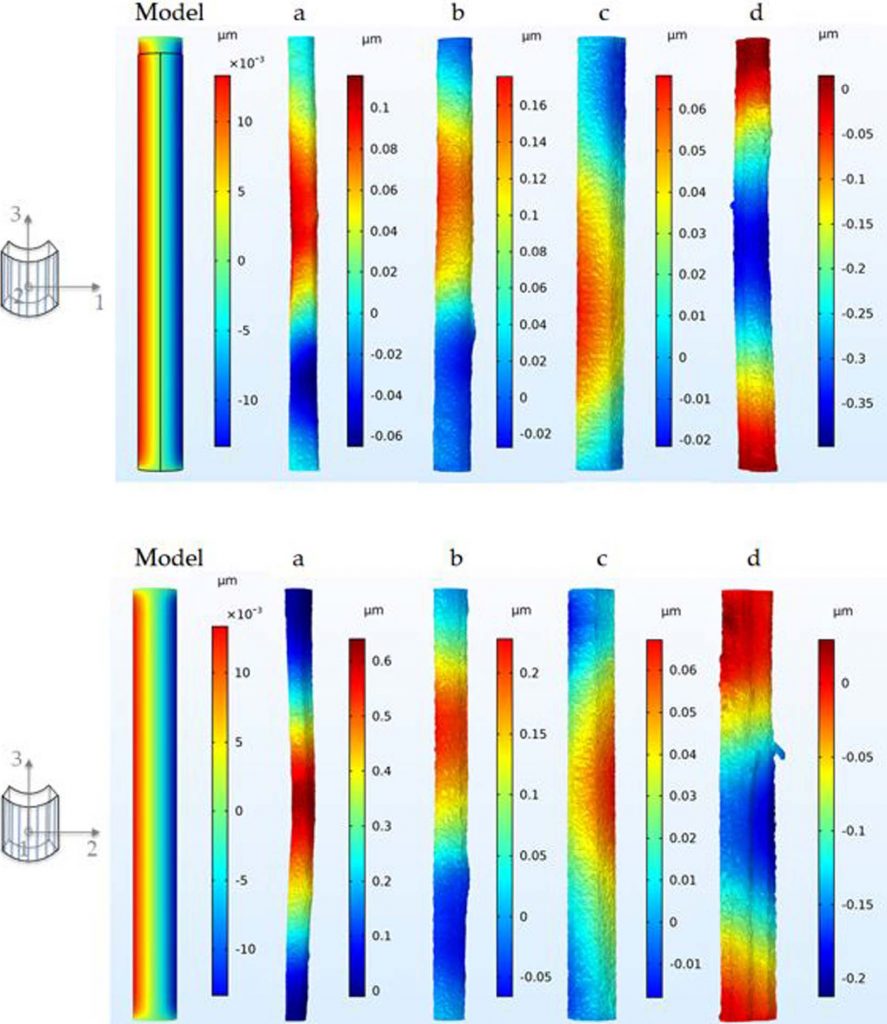
理想化纤维（M）和沿长度无形态变化纤维（-NV）的模拟计算杨氏模量与孔隙率呈完美线性关系。低孔隙率（通常 < 10%）情况下，模量降低仅受孔隙体积分数影响且呈线性关系，因为主导变形机制为拉伸而非孔隙引发的弯曲。

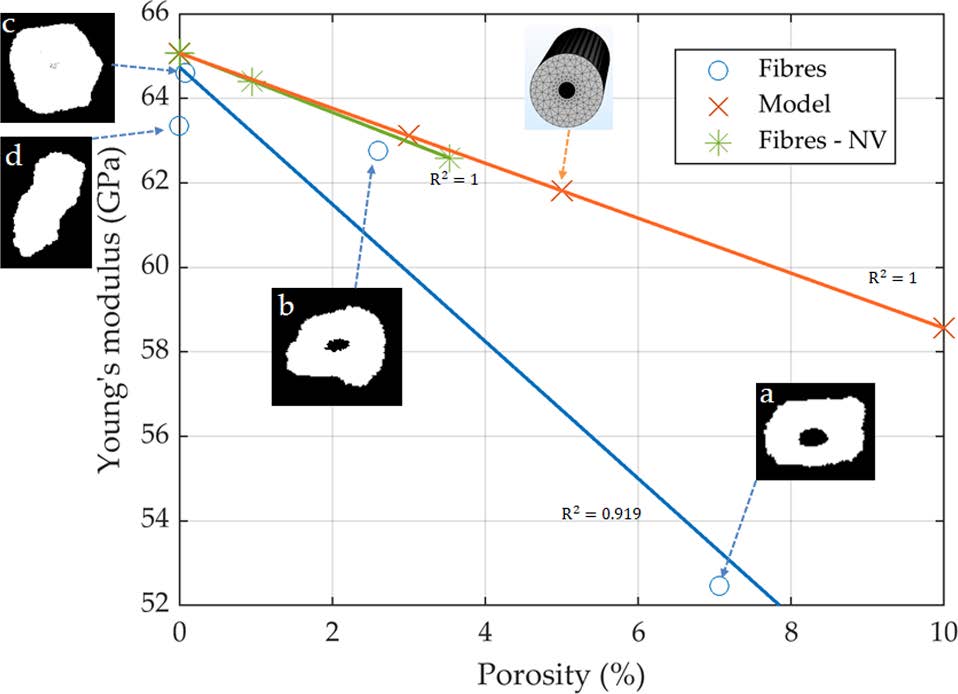
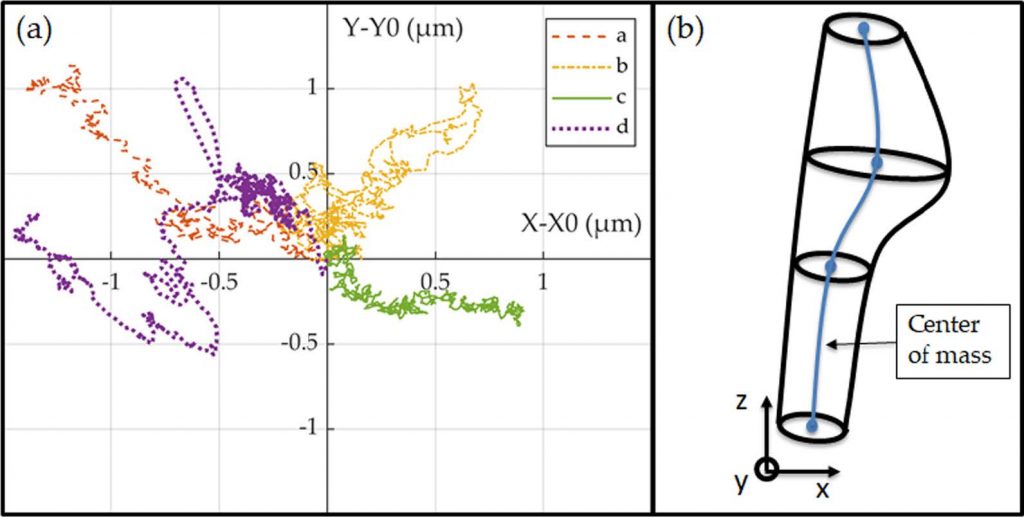
对于沿长度存在形态变化的纤维，杨氏模量随孔隙率增大而下降得更快（斜率增大）。绘制纤维横截面质心位置的演化，纤维 a 和 d 的偏移最显著。尽管加载模式为单轴拉伸，几何因素仍诱导剪切应力。由拉伸方向反作用力计算得出的模量并非纯粹纵向模量，而是轴向与剪切应力共同作用的结果。

应力异质性

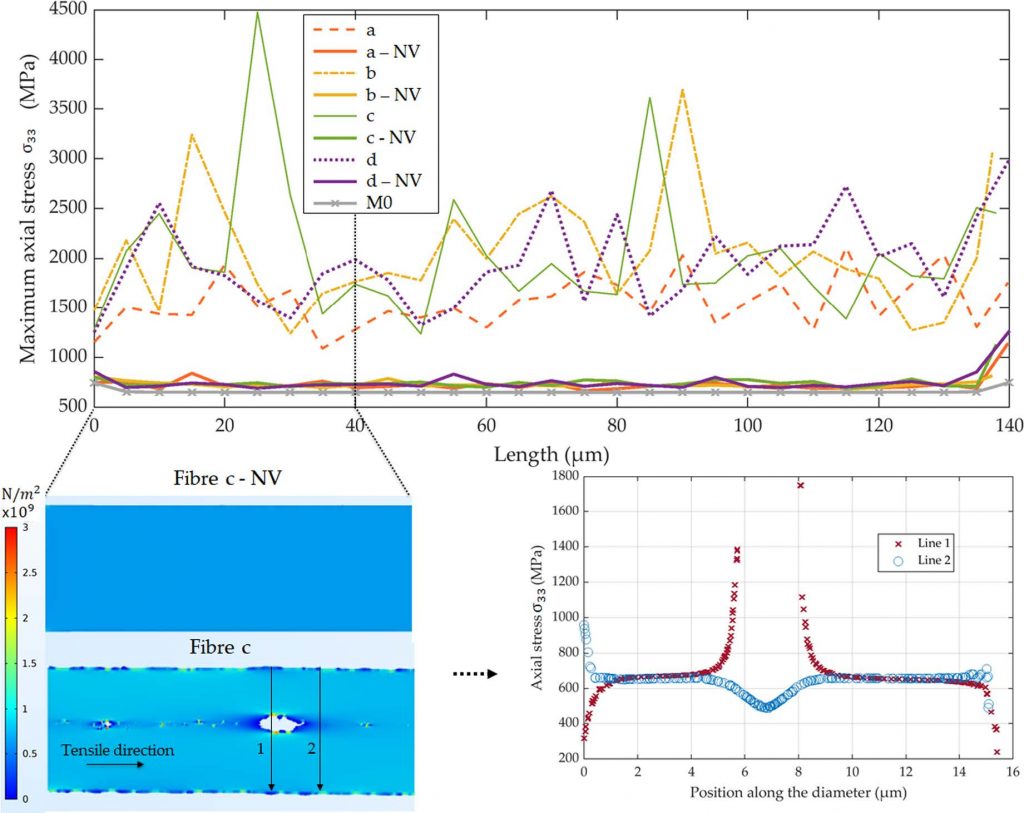
所有纤维整体体积内的平均轴向应力 σ₃₃ 在拉伸方向上较为接近，但其分布异质性因纤维而异。纤维 a-d 因表面粗糙度、外轮廓及内腔形态沿长度变化，剪切应力 σ₁₃ 和 σ₂₃ 非均匀性显著，均呈现正负交替分布。

为量化主导拉伸测试应力分量的集中程度，沿纤维（12 平面）每隔 5 µm 选取横截面，绘制应力峰值及局部关键区域的应力场。结果显示，纤维 a-d 高度轴向应力集中，纤维 c 在特定位置峰值达 4500 MPa。尽管线弹性假设导致该值偏离实际，但仍揭示表面粗糙度与复杂内腔形态共同引发的应力集中。与之相比，无形态变化纤维（-NV）在排除边界效应后，最大轴向应力稳定于 750-850 MPa。

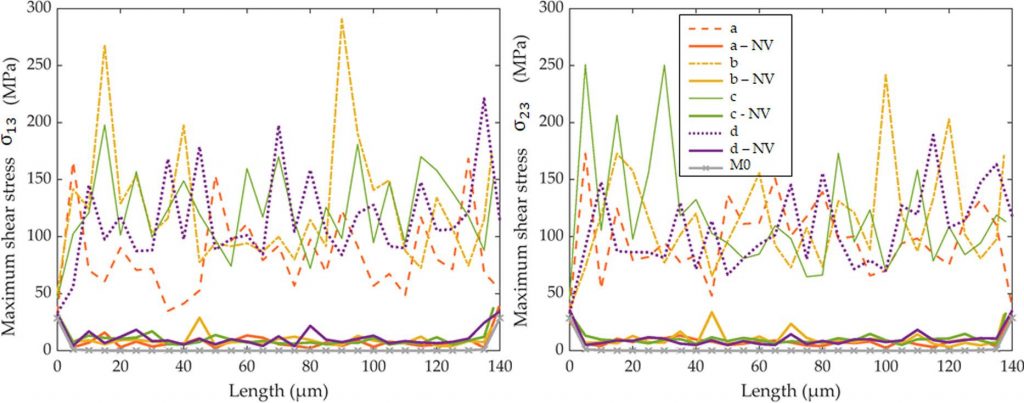
与轴向应力类似，纤维形态沿长度的变化似乎增强了剪切应力场的非均匀性，峰值介于 50-250 MPa，显著高于无变化纤维（-NV 及 M-0）的 35 MPa上限。综上，表面粗糙度、内腔复杂形态及缺陷区微孔可能通过不同加载路径（剪切或拉伸）竞争主导纤维失效，具体取决于根据 Griffith 准则裂纹尖端扩展所需能量。

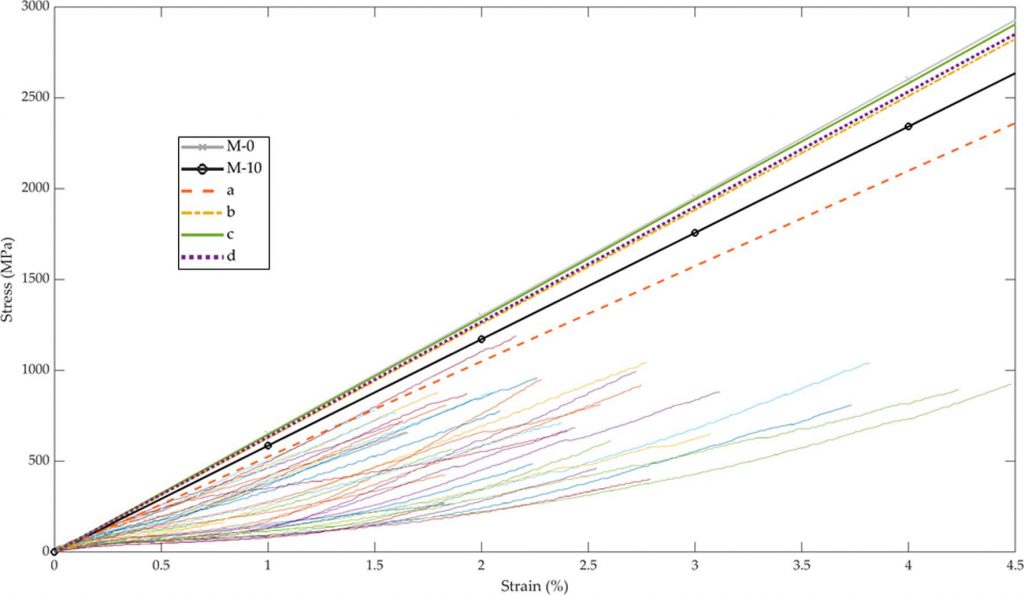
比较实验和有限元模拟获得的纤维应力-应变曲线，孔隙率差异及拉伸载荷下几何因素诱导的剪切应力可以部分地解释实验观测到行为的离散性。相较于实验数据，模拟的杨氏模量被高估，模型因强假设（线弹性、微纤丝角为 0°）未考虑非线性。

总结

本研究基于 μCT 扫描数据创建亚麻纤维的微观结构模型，通过有限元分析探究复杂形态对拉伸性能的影响。未来的工作可以通过实验研究拉伸试验中微纤丝取向和重取向，并将其纳入模型以更好地拟合实验数据。进一步的研究可考虑其他现象如粘性和塑性行为，以及其他反映复合材料零部件寿命期间遇到各种条件的机械载荷和环境类型。

参考

• Richely E, Bourmaud A, Dhakal H, et al. Exploring the morphology of flax fibres by X-ray microtomography and the related mechanical response by numerical modelling[J]. Composites Part A: Applied Science and Manufacturing, 2022, 160: 107052.

---