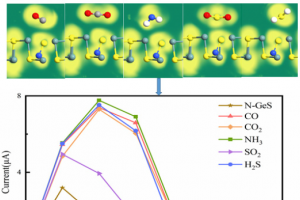
QuantumATK 因其在材料电子态、输运性质和分子动力学性质等方面有丰富的模拟工具箱,特别适合研究这类气敏材料和器件特性,包括: 检测分子在材料上的吸附和脱附 使用过渡态搜索或分子动力学方法研究 吸附导致的电输运特性变化 构造器件构型,直接计算体系电流变化与影响因素 相关机理的探讨 丰富的电子态投影、电荷分析、结构分析等手段,帮助理解机理 Biaxila 应变调控 C5N 基二维器件高各向异性气敏性能:第一性原理研究 二维氮化碳材料因其丰富的元素资源、高物理化学稳定性和优异的电子性能,被广泛应用于器件制备、气体吸附与分离等诸多领域。本文采用密度泛函理论和非平衡格林函数方法,研究了 C5N 基结构的电子结构、输运特性和气体灵敏度。结果表明,电子输运表现出明显的各向异性,其中扶手椅型方向的电子输运比锯齿型形方向的电子输运更具导电性。值得注意的是,两个方向都存在负微分电阻效应。此外,还研究了吸附在 C5N 单层上的无机分子(NO、CO、NO2、SO2 和 NH3)的输运和传感特性。结果表明,CO、SO2 和 NH3 以物理吸附的形式存在于C5N表面,而 NO 和NO2 则以化学吸附的形式粘附在 C5N 表面。设计的C5N 气敏传感器对 NO 和 NO2 分子表现出很高的灵敏度,在 0.1 V 偏压下对 NO2 的灵敏度达到81%。最后研究了应变对气敏器件吸附性能的影响。研究表明,在扶手椅方向施加 -4% 的应变可以明显增加 NO 和 NO2 的电流,显著提高气敏器件的性能。无论是对器件施加应变还是气体吸附,C5N 材料始终保持明显的各向异性。本研究表明 C5N 是一种高度各向异性和灵敏性的二维材料,在电子特性和气体传感领域有着广阔的应用潜力。 Li, H., Liu, Z., Liu, G., Yang, N., Wu, […]
考虑自旋轨道耦合的二维范德瓦尔斯铁电半导体中可调的自旋体光伏效应
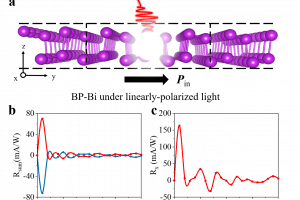
背景介绍 体光伏效应是一种特殊的非线性光学效应,它可以让在中心反演对称性破缺的体系中受到光照后产生直流电,这种效应和二次谐波效应(产生交流电)也具有密切的关系。自旋体光伏效应是体光伏效应的一种衍生子效应,特指材料在被光照射后可以产生自旋流。要产生自旋体光伏效应的核心是自旋-动量锁定,而考虑相对论效应则是最直接的一种实现自旋-动量锁定的方法。在本文中,作者系统地总结了由于相对论效应产生的自旋体光伏效应的机理,并通过对称性分析和第一性原理量子输运方法研究了在铁电调控下这些自旋流的调制情况。 研究内容 近日,北京大学物理学院吕劲课题组在Phys. Rev. B上发表了题为“Tunable spin photogalvanic effect in two-dimensional van der Waals ferroelectric semiconductors with spin-orbit coupling”的工作,该工作系统性地研究了由于自旋轨道耦合效应导致的自旋体光伏效应在范德瓦尔斯铁电材料中受铁电调控的一般情况。并且在研究面内铁电极化时发现一种全新的物理现象,即调控体系的铁电极化方向后,光激发的自旋流不发生改变,但电荷流的方向发生改变,作者将这种全新的现象命名为“隐藏的自旋流调控”效应。 本文中的相对论性第一性原理量子输运模拟是由QuantumATK实现(采用了相对论性的赝势和原子轨道基的结合),本文的结果表明了使用量子输运方法研究特定体系的输运性质(包括非线性光学效应)已经成为了继密度泛函微扰理论之后的又一有力工具。本文的第一作者为课题组博士方世博,通讯作者为北京大学物理学院罗昭初研究员和吕劲研究员。 以下是使用QuantumATK计算的自旋体光伏的电荷流和非共线自旋流性质,文中考虑了三种二维材料中的铁电调控情况,分别是面内铁电材料(BP-Bi为例): 面外铁电材料(α-GeTe为例): 和面内面外耦合的铁电材料(α-In2Se3): 总结: 该工作系统地提出了一个模型,用于描述自旋-光电旋效应(SPGE)在自旋轨道耦合(SOC)铁电半导体中的行为,考虑了一阶相对论扰动(Rashba效应),包括平面内、平面外和平面内-平面外耦合的自旋轨道耦合。在平面内铁电材料中,可以通过调节铁电性质来调制Sz分量的自旋电流,但不能通过圆偏振光来实现。在平面外铁电材料中,无论是线偏振光还是圆偏振光都可以通过调节铁电性质来调制Sx和Sy分量的自旋电流。在耦合铁电材料中,无论入射光的类型如何,都可以通过铁电性质有效地控制自旋电流的所有三个分量。通过采用第一性原理计算和量子输运,该文使用BP-Bi、α-GeTe和α-In2Se3这三个案例验证了这个模型。结果表明,当忽略高阶相对论扰动时,该模型是成立的。然而,当铁电材料受到来自高阶相对论效应(Dresselhaus效应)的扰动时,需要对模型进行特定修改。这项工作为未来关于电-光-磁耦合新型存储器的研究铺平了道路。 参考文献: Tunable spin photogalvanic effect in two-dimensional van der Waals ferroelectric semiconductors with spin-orbit coupling. Phys. Rev. B 109, 195202 (2024); DOI:https://doi.org/10.1103/PhysRevB.109.195202
基于Janus-MoSSe和C3N4构建的范德华异质结中的可调节能带排列和光学特性
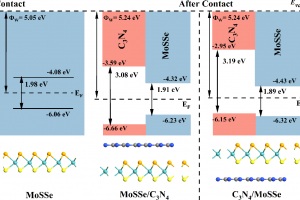
背景简介 具有可调节能带排列的范德华异质结被认为是未来制造高性能多功能纳米光电器件的理想候选材料。在半导体与半导体结合构建的异质结构中具有多种能带排列方式,包括I型(跨接)、II 型(交错)以及 III 型(断隙)。I 型异质结构中的电子和空穴都位于同一种半导体材料中,这将有利于载流子的快速复合,这一特性使得I型异质结通常用于发光器件中。而在II型异质结构中,电子和空穴则位于不同的半导体材料,这种空间上的分离能够有效抑制载流子的复合并延长层间激子寿命,因而在太阳能器件中得到广泛应用。对于III型异质结构,由于两种半导体材料的价带和导带相互重叠,导致III型异质结构具有更高的电子隧穿概率。因此,实现异质结构的可调节能带排列是制造高性能的多功能纳米光电器件的前提。然而,目前大多采用调节异质结构的构成层成分或者厚度的方法来实现能带排列方式的变化,显然这些方法难以在实验中实现。 研究内容 由于具有 S 原子和 Se 原子两个不同的表面,因此 Janus-MoSSe 两表面的电势并不相同。基于 MoSSe 的这种特性并考虑 C3N4 相对 MoSSe 的不同旋转角度,通过结合能的计算获得最稳定的 MoSSe/C3N4(C3N4-Se)和 C3N4/MoSSe(C3N4-S)异质结构,并进行相关性质的研究。研究表明,由于两种异质结构内建电场强度的不同(图1c-d)导致构成层的能带边缘位移的差异(图2),MoSSe/C3N4 异质结构呈现出I型能带排列特征,这将适用于发光器件中,C3N4/MoSSe 异质结构呈现出II型能带排列特征,这将有利于载流子的分离并在太阳能器件中具有较大应用潜力。相较于目前调控异质结构能带排列方式的手段,这种通过切换异质结构堆叠方式来实现的方法,将更容易在实验中实现。此外,这两种异质结构的能带排列方式可以通过外加电场进行调节,即在I型和II型能带排列之间转换。另一方面,两种异质结构在原始状态下的主要吸收峰都位于可见光区(~2.9eV),通过施加正(负)方向电场,吸收峰的峰值可以得到增强(减弱),这一特征使得 MoSSe/C3N4 和 C3N4/MoSSe 异质结构可以应用于光调制器中。这些研究结果表明,MoSSe/C3N4 和 C3N4/MoSSe 异质结构在多功能电子器件(包括发光器件、太阳能器件、光调制器等)中具有巨大的应用潜力。 图1 MoSSe/C3N4 和 C3N4/MoSSe 异质结构的(a-b)层相关的投影电子能带结构和(c-d)沿z方向的有效势。 图2 MoSSe/C3N4 和 C3N4/MoSSe 异质结构的能带排列和功函数示意图。ΦW、Evac 和EF 分别表示功函数、真空能级和费米能级。真空能级设置为零。 总结 基于 Janus-MoSSe 的面外不对称性,将 C3N4 分别放置在MoSSe 的不同侧面构建出 MoSSe/C3N4(C3N4-Se)和 C3N4/MoSSe(C3N4-S)异质结构,以此希望通过更为简便的方法实现异质结构能带排列方式的转换和更强的光学性能。由于 MoSSe 两侧原子的势能差异,两种异质结构的内建电场强度并不相同,导致其构成层能带边缘的位移程度也存在差异,最终 MoSSe/C3N4 […]
新的低成本 Meta-GGA 泛函计算获得正确带隙(Phys Rev Mater. 2023)
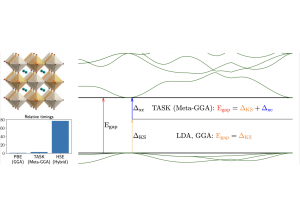
摘要 对于新材料的发现,准确快速地预测带隙非常重要,密度泛函 LDA 和 GGA 虽然效率很高,但是系统性地倾向于低估带隙,其根本原因在于忽略了 ∆xc 导数的不连续性问题。带隙的可靠预测,通常需要求助于计算上更昂贵的杂化泛函,或超越 DFT 方法如 GW 计算。不过对材料筛选或大型复杂体系,这些方法通常在时间成本上无法承受。 最近的一项研究中,研究人员发现 Meta-GGA 中的 TASK 泛函[1](AMS2023 以后的版本包含该泛函)可以相当好地兼顾精度和计算速度[2]。Kohn-Sham 和广义 Kohn-Sam 计算结果比较表明, TASK 来自正确的理论,即,适当结合 Kohn Sham 间隙 ∆KS 和 ∆xc 导数不连续性的贡献,能够得到正确的带隙。即使对于卤化物钙钛矿等复杂材料,TASK 也预测出类似于混合 HSE[3] 的带隙,但值得注意的是,TASK 的效率却不是 HSE 能比的。在其他设置相同的情况下进行带隙计算,数值稳定的 Meta-GGA TASK 的效率通常是 GGA 的1/3,但比杂化泛函快 20-30 倍。 Meta-GGA TASK 可直接在 AMS 中的 Libxc 中调用。另外,与其他 Meta-GGA 不同,TASK 对原子径向网格的密度要求比其他 Meta-GGA 低。此外,虽然带隙通常使用广义 Kohn-Sham 计算,但 […]
新型二维材料 $\mathrm{WSi}_2\mathrm{N}_4$ 亚5纳米门长晶体管的性能极限(Phys. Rev. Appl. 2023)
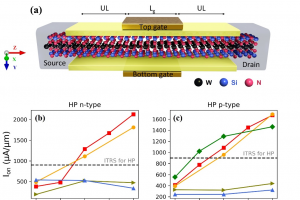
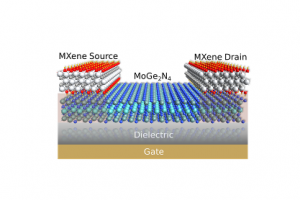
简介 构建互补金属氧化物半导体(CMOS)器件需要 n 型和 p 型金属氧化物半导体场效应晶体管(MOSFETs)。但在超短栅长情况下寻找一种 n 型掺杂和 p 型掺杂同时满足国际半导体技术路线图(ITRS)标准的沟道材料仍然是一个挑战。最近合成的二维晶体 $\mathrm{WSi}_2\mathrm{N}_4$ 具有较高的空穴和电子载流子迁移率,为这一问题提供了可能的解决方案 [Science, 2020, 369 (6504), 670-674]。北京大学物理学院吕劲课题组使用第一性原理密度泛函理论(DFT)和非平衡格林函数(NEGF)方法,探讨了双栅单层 $\mathrm{WSi}_2\mathrm{N}_4$ MOSFETs 在亚 5 nm 栅长下的性能极限 [Phys. Rev. Appl., 2023, 20 (6), 064044]。这项研究显示,n型和p型双栅单层 $\mathrm{WSi}_2\mathrm{N}_4$ MOSFETs 可将满足ITRS高性能(HP)标准的门长尺寸缩短为 3 nm,开态电流高度对称。在功耗延迟积(PDP)与延迟时间($\tau$)的多目标优化 Pareto 边界分析中,n 型单层 $\mathrm{WSi}_2\mathrm{N}_4$ 晶体管处于典型二维材料中最优平衡的 Pareto 边界上。显示了单层 $\mathrm{WSi}_2\mathrm{N}_4$ 作为下一代 CMOS 器件沟道材料的潜力。考虑温度和无序的影响,模拟结果仍然适用。该项工作于今年12月发表在 Physical Review Applied 上,北京大学物理学院博士生黎颖为第一作者,北京大学物理学院吕劲研究员和洛阳师范学院化学化工学院副教授、哈佛大学 John A. Paulson 工程与应用科学学院访问学者孙晓甜为共同通讯作者。 研究内容 本研究通过掺杂浓度和欠叠层结构对亚 5 nm […]
范德华多铁隧道结中面向存算一体的磁电协同控制多级导电态(Nanoscale 2024)
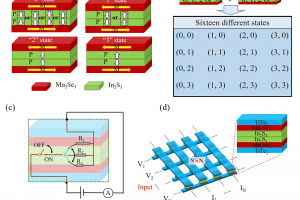
研究简介 范德华多铁隧道结有望实现小型化、高密度和非易失性存储,在下一代数据存储和存算一体器件中具有巨大应用潜力。福州大学材料科学与工程学院萨百晟课题组联合北京航空航天大学和华中科技大学,采用结合密度泛函理论与非平衡格林函数结合的计算方法,模拟了由铁磁半金属材料 $\mathrm{Mn}_2\mathrm{Se}_3$ 作为自旋过滤势垒,金属材料 $\mathrm{Ti}\mathrm{Te}_2$ 作为电极,铁电材料 $\mathrm{In}_2\mathrm{S}_3$ 作为隧道势垒组成的范德华多铁隧道结器件的自旋输运性质。器件采用双层 $\mathrm{In}_2\mathrm{S}_3$ 作为隧道势垒时可以同时实现显著的隧道磁阻和隧道电阻效应,在非零偏压下,最大隧道磁阻和电阻比率分别可达6237%和1771%。进一步发现在该多铁隧道结内存在四种可区分的电导状态,即仅需一个多铁隧道结单元就可实现四态非易失性数据存储。且通过等效的磁、电开关可以分别控制器件电流的通断和大小,通过搭建多铁隧道结阵列可同时实现逻辑计算和多级数据存储。这些研究结果揭示了该隧道结在存算一体以及多级数据存储器件中的潜在应用。福州大学材料科学与工程学院博士研究生崔舟为第一作者。该研究得到了国家重点研发计划与国家自然科学基金的资助支持。 研究内容 利用QuantumATK软件,以单层铁电材料 $\mathrm{In}_2\mathrm{S}_3$ 作为势垒层,具有金属性质的 $\mathrm{Ti}\mathrm{Te}_2$ 作为电极材料,搭建了如图1所示的器件模型,图1(a)和(b)中显示了 $\mathrm{In}_2\mathrm{S}_3$ 的两种不同极化方向的情况,在考虑铁磁层磁矩的方向后,单层 $\mathrm{In}_2\mathrm{S}_3$ 器件理论上可以实现四种导电状态。图1(c-f),进一步计算了器件不同状态下的透射系数曲线和费米面处的透射谱,并且统计了各种状态下的费米面出的隧穿磁阻率和隧穿电阻率。对于单层 $\mathrm{In}_2\mathrm{S}_3$ 器件最大可以实现448%隧穿磁阻率,但是其最大的隧穿电阻率仅有30%。 图1 单层 $\mathrm{In}_2\mathrm{S}_3$ 作为隧道势垒的多铁隧道结在(a)FE-R-1IS和(b)FE-L-1IS状态下的结构示意图。(c)FE-R-1IS和(d)FE-L-1IS状态下多铁隧道结自旋分辨的零偏压透射系数曲线。(e)FE-R-1IS和(f)FE-L-1IS态下多铁隧道结自旋分辨的透射谱。 将单层 $\mathrm{In}_2\mathrm{S}_3$ 势垒层替换为双层 $\mathrm{In}_2\mathrm{S}_3$ 后,如图 2 所示,不同状态下的透射系数曲线和费米面处的透射谱具有更明显的差异。对于双层$\mathrm{In}_2\mathrm{S}_3$ 器件可以实现最大的隧穿磁阻率为5698%,最大隧穿电阻率为1771%。从费米能级处的透射谱可以得知,高的隧穿磁阻率和隧穿电阻率主要是由于平行磁阻态下的自旋向上电子的透射能力具有显著差异。 图2 双层 $\mathrm{In}_2\mathrm{S}_3$ 作为隧道势垒的多铁隧道结在(a)AFE-T-2IS,(b)AFE-H-2IS,(c)FE-R-2IS和(d)FE-L-2IS状态下的结构示意图。(e)AFE-T-2IS,(f)AFE-H-2IS,(g)FE-R-2IS和(h)FE-L-2IS态下多铁隧道结自旋分辨的零偏压透射系数曲线。(i)AFE-T-2IS,(j)AFE-H-2IS,(k)FE-R-2IS和(l)FE-L-2IS态下多铁隧道结自旋分辨的透射谱。 为了进一步探究这种差异的原因,计算了双层 $\mathrm{In}_2\mathrm{S}_3$ 作为隧道势垒的多铁隧道结在各种状态下 $\mathrm{Mn}_2\mathrm{Se}_3$ 和 $\mathrm{In}_2\mathrm{S}_3$ 层的态密度。从图3中可知,由于受到 $\mathrm{Mn}_2\mathrm{Se}_3$ 铁磁层的影响,$\mathrm{In}_2\mathrm{S}_3$ 层在费米面处产生了新的态密度,这是造成器件导电能力不同的主要原因。最后本文阐述了器件可能应用的方向。双层 $\mathrm{In}_2\mathrm{S}_3$ 器件的八个导电状态可以简并为如图4(a)所示的四种可显著分辨的导电状态,仅用两个隧道结单元就可以实现十六种存储状态,用于多态存储,如图4(b)所示。另外,可以将一个隧道结单元等效成为一个磁电开关,用磁场开关控制电路的通断,电场开关控制电流的大小,如图4(c)所示。将多个隧道结单元排列成如图4(d)所示的 N×N 阵列,在输入端加一系列电压,根据基尔霍夫定律和欧姆定律,在输出端可以得到一系列电流,从而完成一次乘法累加运算。由于每个多铁隧道结本身具有数据存储的能力,这样就可以将“存”和“算”集成在同一器件单元上,实现存算一体。 图3 双层 $\mathrm{In}2\mathrm{S}_3$ 作为隧道势垒的多铁隧道结在(a)AFE-T-2IS,(b)AFE-H-2IS,(c)FE-R-2IS和(d)FE-L-2IS状态下各个 $\mathrm{Mn}_2\mathrm{Se}_3$ […]
铁电调控的双向光响应器件:基于Van der Waals α-In2Se3/NbX2(X = S, Se和Te)铁电二极管
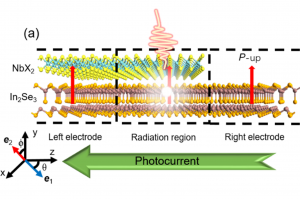
简介 双向光电探测器是指在外部刺激下,其光电流可以在不同方向之间切换的设备。在神经形态视觉系统中,单个双向光电探测器可以分别表示兴奋和抑制行为中的正负权重,从而大大减少了人工神经网络中的硬件数量。现有的可调双向光电检测主要依赖于二维材料中的门控带对齐和金属与半导体复合系统中的光热效应。然而,门控工程的要求必然消耗额外的功率,并且光热效应的响应时间过长。 铁电二极管是一种特殊的二极管,其整流方向可以通过极化反转进行切换。基于铁电氧化物的传统体积型Fe二极管可以通过轻松切换其电极化方向来产生非易失的对称双向光响应。这种切换过程具有超快的动力学响应(<1纳秒)和高度可控性,无需持续的电压供应。切换机制源于由极化引起的表面电荷调制的肖特基势垒的高度(SBHs)和内建电场。然而,现有的铁电二极管还主要是基于传统的铁电氧化物材料,在实际应用中存在着较为严重的界面缺陷。 研究内容 利用QuantumATK软件,作者首次使用第一性原理结合量子输运的方法模拟了二维范德瓦尔斯型α-In2Se3/NbX2 (X = S,Se和Te) 铁电二极管的电学传输和光电输运性质。作者通过计算器件的局域器件态密度发现,可以通过调控α-In2Se3的铁电极化方向使器件从一个p-i结转化为一个n-i结,因此其整流方向就会发生转变,从而实现非易失性存储功能和双向光响应效应。作者的工作揭示了vdW Fe二极管在未来计算-传感器架构中具有巨大潜力。 图1. α-In2Se3/NbX2(X=S、Se和Te)铁电二极管中(a)向上极化和(b)向下极化态双向光电流的基本原理 图2. α-In2Se3/NbS2-Fe二极管的局域器件态密度(a)P向上和(b)P向下。子图(c)和(e)与(a)相同,但X分别为Se和Te。子图(d)和(f)与(b)相同,但X分别为Se和Te。每个子图中的两条水平白色虚线之间的距离表示铁电能带偏移(EFE)。中心区域和电极区域由垂直的白色虚线分隔开。 图3. (a) vdW α-In2Se3/NbS2铁电可开关二极管在不同铁电极化和沿y轴以偏振角θ入射的线偏振光下的光响应。子图(b)和(c)与(a)相同,但分别用于NbSe2和NbTe2。子图(d)与(a)相同,但对于沿着z轴入射的具有偏振角Φ的线偏振光。子图(e)和(f)与(d)相同,但分别用于NbSe2和NbTe2。 参考 Fang, S.; et al. Phys. Rev. Mater. 2023, 7 (8), 084412. https://doi.org/10.1103/PhysRevMaterials.7.084412.
探索氢键对低维材料金半接触中的性能提升与理论极限(Mater. Horiz. 2023)
简介 超越硅材料的先进电子学发展需要将沟道材料厚度缩减至二维(2D)极限。然而,利用 2D 半导体制造器件的一个关键挑战是需要接近量子极限的低接触电阻,这主要受限于固有的范德华间隙导致的附加隧穿电阻。最近,半金属(铋、锑等)/二硫化钼接触的强范德华接触接近量子极限,为进一步缩小器件尺寸和延续摩尔定律提供了希望,引发了一波探索 2D 晶体管性能极限的研究热潮。然而,继续降低接触电阻仍然具有挑战性,因为半金属接触受限于范德华相互作用的本质及狭窄的功函数范围。此外,实现清洁无损的金属沉积工艺仍具有一定技术挑战。因此,急需实现能本质上克服范德华间隙的超洁净、无损的金半接触。北京大学信息工程学院张敏课题组利用第一性原理和量子输运模拟,提出与阐明了氢键接触技术在开发新型低维器件和探索性能极限中的潜力,凸显了化学、物理和材料科学之间的交叉研究对电子学发展的重要机遇。 图1. 氢键接触的概念图 图2. 氢键异质结中洁净且紧密的金半接触 研究内容 这项研究基于第一性原理提出利用氢键相互作用本质上克服固有的范德华间隙,并讨论了在各种 2D 半导体中实现良好氢键接触的通用设计理念。鉴于氢键所具备的类似于范德华力的洁净界面特性,且具有更强的电子态耦合能力,氢键接触能够实现接近量子极限的超低接触电阻。此外,2D 材料的表面工程赋予了氢键接触较高的设计灵活性,能够使金半接触同时逼近修正的肖特基-莫特极限。理论预测优异的氢键接触可以为各种新型高迁移率 2D 半导体(如氮化物、氧化物、卤化物、硫族化合物等)提供延续摩尔定律所需的电接触。这项研究成果将为进一步探索 2D 晶体管的性能极限提供理论指导,并为从高性能晶体管到量子器件的广泛应用提供了一种设计理想金半接触的方法,从而加速这个令人兴奋且迅速发展的领域的进步。 图3. 氢键接触在十余种二维半导体中同时实现量子极限和修正的肖特基-莫特极限 图4. 氢键异质结的动力学结构稳定性分析 本研究进一步利用 QuantumATK 中的机器学习力场模块研究了复杂的氢键接触体系的动力学稳定性,在理论上指出了最有利于实验实现的材料组合。使用 QuantumATK 中的 Nudge Elastic Band 模块计算了氢键异质结中氢原子的扩散势垒来进一步评估氢键接触的化学稳定性。研究结果表明,氢原子扩散势垒的高度与异质结的接触性能之间存在权衡。具体来说,随着异质结结合能的增加,两种材料之间的接触会变得更紧密,并表现出更大的隧道概率。因此,这导致氢原子的扩散阻力降低。为了在接触性能和稳定性之间取得平衡,作者重点研究了 Nb4C3(OH)2/MoS2 异质结,它的扩散势垒为 0.94 eV,同时接触电阻较低(n2D = 1.5×1013 cm-2 时为 109.82 Ω μm;n2D = 3×1013 cm-2 时为 57.31 Ω μm)。 为了量化温度效应导致的接触几何形状对电接触的影响,作者利用 QuantumATK 的分子动力学模块在进行长达 100ps 的NVT热平衡之后独立进行了多个时长为 5ps 的 Langevin 动力学采样。由于粒子的初始速度是从随机麦克斯韦分布中产生的,因此对多个样本的结果取平均值可确保在给定温度下产生具有统计学意义的结果。这种方法已被广泛用于解决电子-声子耦合问题(如 Phys. Rev. B, 2017, […]
H-diamond/h-BN中层间转角调控的界面特性
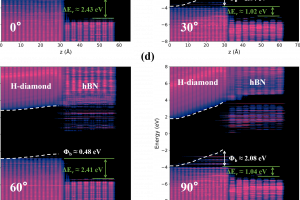
简介 层间转角作为一种全新的调控自由度,为新奇的强关联物理现象提供研究平台的同时,也为混合维度范德华(vdW)异质结界面特性的调控提供了新的思路。在本文中,西安电子科技大学张进成老师课题组基于QuantumATK中密度泛函理论(DFT)和非平衡格林函数(NEGF)耦合的方法,研究了层间转角对H-diamond/h-BN vdW异质结界面处载流子行为和能带对齐特性的调控机理。结果表明,层间转角为h-BN引入的可控应变将诱导其重杂化并产生额外的自由轨道。此外,层间转角可以通过改变堆垛模式实现对异质结特性的调控。在这两个因素的共同作用下,H-diamond/hBN异质结的vdW耦合强度,电荷转移程度,带隙,界面势垒和价带带阶都可以通过组分间的相对转角进行调控。 层间转角调控下H-diamond/h-BN界面的载流子行为 当层间转角为30°或90°时,严重的晶格失配将为h-BN引入8.56%的压缩应变,此时抗弯刚度较差的h-BN向面外方向弯曲以释放所受应力。屈曲h-BN与H-diamond间的电荷转移程更高,这源于sp2到sp3的轨道重杂化所产生的额外自由轨道。剧烈的电荷转移有助于确保2DHG与维持系统电中性所需的负电荷在空间上充分分离,有效屏蔽了表面杂质散射对2DHG迁移率的影响。 由于倏逝波函数从h-BN向H-diamond表面的渗透,h-BN在H-diamond的导带中引入了额外的能带。其中平面h-BN为H-diamond引入的额外能带局域在H-diamond的CBM附近,而屈曲h-BN引入的额外能带则广泛分布在H-diamond的整个导带中,这表明屈曲h-BN和H-diamond之间的杂化更为强烈。 层间转角调控下H-diamond/h-BN界面的能带结构 四种特定层间转角下H-diamond/h-BN异质结的VBM均由H-diamond贡献,而CBM则由h-BN主导,四种构型均表现出II型异质结的特性。电子和空穴在空间上的充分分离有助于降低载流子输运过程中所遭受的库仑散射,这对保障H-diamond表面高迁移率的2DHG意义重大。 层间转角调控下H-diamond/h-BN界面的能带对齐方式 由于界面处剧烈的电荷转移,30°和90°构型的界面势垒分别高达2.04 eV和2.08 eV。此外,相较于30°构型,90°构型中H-diamond表面的价带带边具有更高的状态密度,这意味着该构型下H-diamond表面具有更高的空穴承载能力,该构型更有利于在H-diamond表面形成高密度的2DHG。 参考 Wang, B.; Ning, J.; Zhang, J.; Zhang, C.; Wang, D.; Hao, Y. Twist angle modulated electronic properties and band alignments of hydrogen-terminated diamond (111)/hexagonal boron nitride heterostructures. Appl. Surf. Sci. 2023, 614, 156245. https://doi.org/10.1016/j.apsusc.2022.156245.
滑移顺电特性:过渡金属二硫族化合物双层
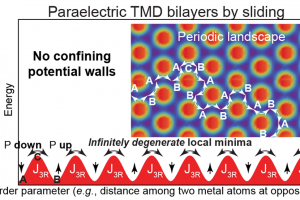
摘要 传统的铁电体经热诱导的相变后结构对称性增加,这种更高对称性结构被称为顺电结构。铁电过渡金属二硫族化合物双层最近被证明是顺电的,但对这种相的原子构型没有太多的描述。采用包括分子动力学在内的数值计算模拟发现,它们的顺电性只能归因于具有相反本征极化的铁电相的时间域平均值,其切换需要宏观上在大的区域里进行一致滑动。 方法 作者对 $\mathrm{MoS}_2$、$\mathrm{WS}_2$、$\mathrm{MoSe}_2$ 和 $\mathrm{WSe}_2$ 等双层进行的研究包含两个部分。第一部分是利用平面波基组密度泛函理论(DFT)计算,得到相对的结构能以及过渡金属二硫族化合物双层的振动特性。另一部分是基于有限温度 MD 计算,采用了机器学习的经典原子间势,这些经典势是采用数值原子轨道基组的 DFT 结果进行训练的。 新一代材料模拟平台 QuantumATK 可以在简单易用的图形界面上完成这类计算的全部计算流程,包括: 支持基于 PAW 势的平面波 DFT 或基于 LCAO 基组的 DFT;计算能量和振动模式;基于 Berry 相位计算极化;直接在图形用户界面上进行 MTP 机器学习势的训练;采用训练好的经典势进行分子动力学模拟。 研究内容 铁电体传统上用具有两个简并极小值的能量图来描述,两个极小值之间存在较小的能量势垒J。3R过渡金属二硫族化合物双层则由于存在周期性的能量势垒结构,成为了一种具有无限数量简并极小值的“不寻常”铁电体。“顺电”状态是极化 P 在长时间内的时间平均值,其中 P 取在任何给定时间交换符号的确定非零值,平均值降到零。 采用机器学习力场的分子动力学模拟 $\mathrm{WSe}_2$双层的滑动(两层间原子对距离随时间的演化)。图 f ~图 i 可以观察到滑动过程。发生滑动的位移方向对应于六角格子的矢量(图 e 插图),通过改变温度直至观察到在 1 微秒内发生滑动,可以确定相转变温度。 490K 温度下的滑动过程 MD 模拟中,可以通过对比滑动前后两帧结构观察到极化的符号翻转。 参考 Juan M. et al. Slippery Paraelectric Transition-Metal Dichalcogenide Bilayers. Nano Letters 2022 […]