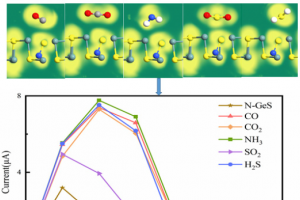
QuantumATK 因其在材料电子态、输运性质和分子动力学性质等方面有丰富的模拟工具箱,特别适合研究这类气敏材料和器件特性,包括: 检测分子在材料上的吸附和脱附 使用过渡态搜索或分子动力学方法研究 吸附导致的电输运特性变化 构造器件构型,直接计算体系电流变化与影响因素 相关机理的探讨 丰富的电子态投影、电荷分析、结构分析等手段,帮助理解机理 Biaxila 应变调控 C5N 基二维器件高各向异性气敏性能:第一性原理研究 二维氮化碳材料因其丰富的元素资源、高物理化学稳定性和优异的电子性能,被广泛应用于器件制备、气体吸附与分离等诸多领域。本文采用密度泛函理论和非平衡格林函数方法,研究了 C5N 基结构的电子结构、输运特性和气体灵敏度。结果表明,电子输运表现出明显的各向异性,其中扶手椅型方向的电子输运比锯齿型形方向的电子输运更具导电性。值得注意的是,两个方向都存在负微分电阻效应。此外,还研究了吸附在 C5N 单层上的无机分子(NO、CO、NO2、SO2 和 NH3)的输运和传感特性。结果表明,CO、SO2 和 NH3 以物理吸附的形式存在于C5N表面,而 NO 和NO2 则以化学吸附的形式粘附在 C5N 表面。设计的C5N 气敏传感器对 NO 和 NO2 分子表现出很高的灵敏度,在 0.1 V 偏压下对 NO2 的灵敏度达到81%。最后研究了应变对气敏器件吸附性能的影响。研究表明,在扶手椅方向施加 -4% 的应变可以明显增加 NO 和 NO2 的电流,显著提高气敏器件的性能。无论是对器件施加应变还是气体吸附,C5N 材料始终保持明显的各向异性。本研究表明 C5N 是一种高度各向异性和灵敏性的二维材料,在电子特性和气体传感领域有着广阔的应用潜力。 Li, H., Liu, Z., Liu, G., Yang, N., Wu, […]
ReaxFF力场、机器学习势、DFTB参数训练工具 ParAMS 正式发布
多尺度全功能的材料与化学模拟平台 AMS AMS 是一款历史悠久而又迅速发展的多尺度全功能的材料与化学模拟平台,目前包括以下功能与应用: 分子体系的量子化学计算:化学反应机理研究、丰富的光谱性质预测、发光、热力学性质、化学键的机理研究、重元素配合物与团簇、多金属氧酸盐、分子构象搜索等 晶体、低维材料:吸附、表面催化、单原子催化、化学反应机理、磁性质、材料电子学性质、化学键的机理研究、力学性能、热力学性质、光的吸收与折射等 介观体系:基于经典力场、反应力场、机器学习势、半经验量子化学方法的分子动力学与蒙特卡洛模拟,被广泛地应用于化学反应机理与预测研究,以及微细加工、燃烧、热解、催化,以及半导体、聚合物物性的研究 宏观物质:离子液体、溶液、气液平衡、液液平衡、共晶、低共熔溶剂等,采用UNIFAC、COSMO-RS/SAC/UNIFAC等方法进行研究,广泛应用于化工、制药领域的研究 更接近实验、工业研究实际:微观动力学、动力学蒙特卡洛 进一步了解,请参考 AMS 的详细介绍(链接)。 ReaxFF力场、机器学习势、DFTB参数的训练工具 AMS 最近几年在参数训练方面发展迅速,AMS2024 版的 ParAMS 功能已经完善,支持导入 ADF、BAND、Quantum Espresso 生成的 DFT 训练集,并方便地从作业中生成键长、能量、电荷、力、Hessian、应力张量、频率、势能面扫描数据,丰富训练集、验证集,甚至可以导入实验数据作为训练集。不仅仅支持训练 ReaxFF 力场,训练 DFTB 的GFN1-xTB、机器学习势 M3GNet 与 NequIP、Lennard Jones 势也大同小异。 训练方法包括:CMAES、Adaptive Rate Monte Carlo、Nevergrad、Scipy、Random Sampling、Grid Sampling。 在训练时,训练集的权重,对训练质量有非常强的影响,ParAMS 能够通过参数敏感度的计算,便于用户衡量需要优化的力场参数、以及训练集的权重。 目前我们提供了完善的训练教程,通过不同的训练方式,展示参数训练时的各方面的功能。 ParAMS 训练的工作思路 使用 DFT 方法,计算相关的体系的各种键长、键角等不同结构下的情况,包括能量、原子电荷、力等,导入 ParAMS 中,作为参考数据,俗称训练集,或者参考集。用户设定好一个初始力场,然后就可以使用 ParAMS 的训练算法,对力场进行训练,得到不同的力场。最终得到一个所谓损失函数最小的力场,就是最佳结果。损失函数用来描述使用力场计算这些体系,与 DFT 计算这些体系,二者之间的差异,差异越小表示力场越优秀。 在训练前,用户也可以根据自己的理解,选择力场中需要训练的参数,并通过 ParAMS 计算一个叫做敏感性的数值。这个数值描述力场参数跟训练集的相关性程度,用户训练时,可以只训练敏感性比较大的参数,敏感度非常小的参数,可以忽略掉,不去训练。并且真正训练时,也可以先训练敏感度最大的少数参数,收敛后固定这些参数,再去训练敏感度稍小一些的参数,这样能够更高效地得到一个优质的力场。 […]
AMS2024 重要新功能概览
基于Advanced WorkFlow模块的ParAMS功能训练功能得到彻底完善,并增加MD Active Learning实时学习AIMD微调或从头训练机器学习势M3GNet与NequIP
清华大学胡憾石、李隽课题组Inorg. Chem. |理论研究揭示二维富勒烯单层的电子结构和化学键
AdNDP轨道、超原子分子轨道(SAMOs)和NOCV轨道作用揭示二维富勒烯单层的电子结构和稳定性 研究背景 自从富勒烯C60被合成以来,富勒烯及其衍生物展现出令人瞩目的化学和物理性质。富勒烯是一种具有Ih对称性的二十面体结构,由20个六边形和12个五边形组成。这种独特的几何结构使它们与传统的纯碳材料如二维的石墨烯和三维的金刚石等材料截然不同。除了单个富勒烯分子外,以C60富勒烯为基本结构单元组装而成的各种碳材料也相继被合成。由于富勒烯封闭的笼状二十面体结构,富勒烯分子也具有很高的稳定性。所以在富勒烯材料中,C60分子之间难以形成强的化学键,主要依靠分子间的范德华(van der Waals)相互作用。例如,面心立方富勒烯晶体(fcc C60)已在室温下被合成,C60质心之间的距离为10.02 Å,其主要作用力为较弱的范德华力。 近年来,具有分子间化学键的富勒烯材料也被科学家们陆续发现。例如,通过[2 + 2]环加成键连接的六方相富勒烯(rhombohedral phase),以及在高温高压下合成的四方相富勒烯(tetragonal phase)等富勒烯固体材料。此外,研究表明,碱金属和碱土金属掺杂可以促进C60聚合物晶体的形成。这些掺杂的富勒烯聚合物展现出丰富的电子性能,有的甚至表现出超导现象。 最近,中科院化学所郑健课题组通过有机阳离子切片策略成功合成了二维单层准六方相富勒烯(qHPC60)和单层准四方相富勒烯(qTPC60)。在二维六方相富勒烯单层中,每个富勒烯被6个相邻的富勒烯碳笼包围,碳笼之间通过碳-碳单键和[2+2]环加成键连接。这种单层富勒烯聚合物的带隙为1.6 eV,具有优异的热力学稳定性,同时表现出优异的光学各向异性、机械性能和热电特性等。此后,关于二维富勒烯材料的实验和理论研究陆续大量报道,但对于这种材料的电子结构与其稳定性的深入探究仍有待进一步明确。 论文详情 清华大学化学系胡憾石、李隽团队采用密度泛函理论方法,通过研究二维富勒烯单层的电子结构和化学键来探讨其稳定性机制。理论计算表明,二维富勒烯单层具有1.46 eV 的直接电子带隙,与实验值(1.6 eV)吻合。研究发现,富勒烯分子间碳-碳键的形成对促进C60之间的电荷流动起着关键作用,使得 C60球内形成双重π芳香性,从而稳定了二维骨架结构。此外,研究还发现二维富勒烯单层内一系列离域的超原子分子轨道(SAMO)。这些轨道表现出类似原子轨道的行为,并杂化形成具有σ/π成键和σ*/π*反键性质的近自由电子带。本研究为理解二维富勒烯单层的电子结构和稳定机制提供了新的见解,对基于SAMO的近自由电子带的二维富勒烯材料的设计和潜在应用提供了理论指导。 该研究成果以“Understanding the Electronic Structure and Chemical Bonding in the 2D Fullerene Monolayer”为题,发表于Inorganic Chemistry期刊。南方科技大学博士后赵晓昆为本文第一作者,清华大学化学系胡憾石和李隽为本文通讯作者。 研究内容 1,二维富勒烯材料的结构和稳定性探究 Figure 1.二维富勒烯材料的结构,(a)俯视图;(b)侧视图。C1,C1′和C2分别代表[2+2]环加成键中的碳原子;C3和C3′分别代表分子间碳-碳单键中的碳原子。 在二维富勒烯材料中,由于C60分子间碳-碳键的形成,导致其内部的C60分子结构发生了扭曲,从Ih对称性降低到了C2h对称性。同时,C60分子内的“56”键和“66”键长的范围分别为1.377-1.610 Å和1.358-1.505 Å;而在原始的C60分子中“56”键和“66”键长分别为1.452和1.397 Å。此外,C60分子间[2+2]环加成键(C1-C1′)和碳碳单键(C3-C3′)的长度均为1.606 Å。对该二维富勒烯材料内部的碳-碳键强度的分析表明,分子间碳-碳键的强度(~ -7.9 eV)要明显小于C60分子内部的碳-碳键强(> -11.2 eV)。对不同温度下(分别为600 K、1000 K、1400 K和1800 K)下时长30 ps 的AIMD模拟结果表明,该材料在1400 K以上仍具有良好的热力学稳定性。然而,在1800 K时,该材料在10 ps的AIMD模拟后会分解成单个的C60分子。 2,二维富勒烯材料的芳香性探究 […]
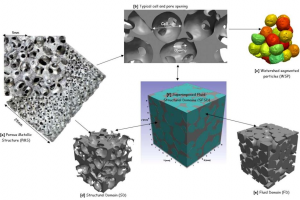
表征微孔结构的有效导热系数:基于三维高分辨率图像的空隙级CFD仿真
本研究通过对孔隙级流体和固体域的三维高分辨率图像处理和计算流体动力学建模与传导传热模拟,估算有效导热系数。
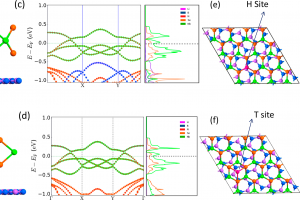
扭转hBN/NbSe2异质结构的电子特性及其在锂离子电池中的应用:第一性原理研究
简介 可用作锂离子电池电极的二维(2D)材料多种多样,但很难有单一材料可以满足所有的综合性能需求。因此,研究的一个努力方向为设计异质结构,从而实现在单一母体结构中不存在的特性。这篇论文报道的工作中,作者设计了一种由导电的2D NbSe2层和绝缘的六方氮化硼(h-BN)制成的范德华异质结构作为锂离子电池中的电极,并考查两种材料层间扭转角度的影响。异质结构实现了金属特性,这使得本来绝缘的h-BN能够应用于电池。吸附位点随扭曲角度的不同而变化。对于5.21°和54.79°的扭转角,H位点是最有利的吸附位点,但对于所有其他扭转角,T位点仍然是最有利吸附位点。当表面之间的角度为19.11°时,在不同的扭曲角度下,与所有其他配置相比,异质结构表现出更好的稳定性。与单个单层相比,吸附能得到增强,表明嵌入效果更好。在19.11°的扭曲角下,结构显示出0.6eV的最小扩散势垒,而在所有其他扭曲角下显示出0.9eV的势垒。开路电压为0.62 V。该结构显示出185 $ \mathrm{mA}~\mathrm{h}~\mathrm{g}~\mathrm{m}^{−1}$的比容量。 研究内容 作者使用 QuantumATK 中的原子轨道线型组合(LCAO)基组方法的DFT对这种异质结构进行了详细的研究。使用 QuantumATK Builder 中的 Interface 工具可以构造任意材料之间的界面,控制晶格试配情况、超胞原子数和晶格张力,并比较了不同扭转角度的结构特征,以及在锂离子嵌入后结构的变化情况,确认19.11°为最好的扭转角度,并研究了扭转角度为 19.11 度时锂离子的嵌入吸附位点。作者通过结构的结合能、形成能以及第一原理的动力学说明了这些结构的稳定性。由体系的吸附结构状况、离子吸附能等信息可以计算出理论的比容量和开路电压。 采用电子分布、电荷布居和态密度投影等手段可以分析锂离子吸附后的构型的电子态。 采用CI-NEB方法可以计算锂离子在其中不同位点间的扩散能垒。 QuantumATK简介 以上是 QuantumATK 在电池材料研究中的一个入门级案例,供材料学计算模拟的初学者参考。实际上,QuantumATK 是一个全集成、全功能的材料与器件模拟平台,用户可以通过友好的图形界面可以直接使用以上多种计算引擎进行材料学模拟研究。QuantumATK 完全基于 Python 开发,用户可以直接编程混合使用其中专有的 Python 类型和更多的开源模块进行二次开发,丰富自己的研究工具箱。 QuantumATK 在整合和改进传统计算方法引擎和材料性质计算模块方面进行诸多有益的尝试,为全流程的材料计算模拟准备好了必要的工具。自有的密度泛函理论(DFT)方法算法可以更好的的平衡计算量和精度,常规DFT计算可以直接模拟数千原子的超大体系,杂化泛函计算速度提升百倍,可以直接计算千原子体系;机器学习力场方法可以在图形界面上操作,实现训练、验证、主动学习和力场应用的全部流程;在性质计算方面,QuantumATK 包含多种复杂物理模型,提供力、光、热、电、磁、电输运等性质的计算模块;独特的双电极器件与栅极器件模型可以直接计算复杂异质结构的伏安特性和转移特性等,是研究纳米电子器件的有力工具;在聚合物材料、电池材料等多领域都提供特殊的模型和方法,更好的模拟贴近实际的材料体系。 更多信息参看费米科技官网: https://www.fermitech.com.cn/quantumatk 参考 Sahoo, S., et al. Electronic Properties of Twisted hBN/NbSe 2 Hetero-Structure and Its Application as an Electrode in Lithium-Ion Battery: […]
考虑自旋轨道耦合的二维范德瓦尔斯铁电半导体中可调的自旋体光伏效应
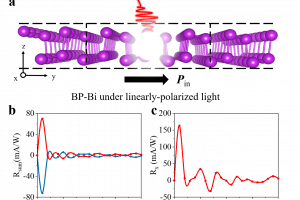
背景介绍 体光伏效应是一种特殊的非线性光学效应,它可以让在中心反演对称性破缺的体系中受到光照后产生直流电,这种效应和二次谐波效应(产生交流电)也具有密切的关系。自旋体光伏效应是体光伏效应的一种衍生子效应,特指材料在被光照射后可以产生自旋流。要产生自旋体光伏效应的核心是自旋-动量锁定,而考虑相对论效应则是最直接的一种实现自旋-动量锁定的方法。在本文中,作者系统地总结了由于相对论效应产生的自旋体光伏效应的机理,并通过对称性分析和第一性原理量子输运方法研究了在铁电调控下这些自旋流的调制情况。 研究内容 近日,北京大学物理学院吕劲课题组在Phys. Rev. B上发表了题为“Tunable spin photogalvanic effect in two-dimensional van der Waals ferroelectric semiconductors with spin-orbit coupling”的工作,该工作系统性地研究了由于自旋轨道耦合效应导致的自旋体光伏效应在范德瓦尔斯铁电材料中受铁电调控的一般情况。并且在研究面内铁电极化时发现一种全新的物理现象,即调控体系的铁电极化方向后,光激发的自旋流不发生改变,但电荷流的方向发生改变,作者将这种全新的现象命名为“隐藏的自旋流调控”效应。 本文中的相对论性第一性原理量子输运模拟是由QuantumATK实现(采用了相对论性的赝势和原子轨道基的结合),本文的结果表明了使用量子输运方法研究特定体系的输运性质(包括非线性光学效应)已经成为了继密度泛函微扰理论之后的又一有力工具。本文的第一作者为课题组博士方世博,通讯作者为北京大学物理学院罗昭初研究员和吕劲研究员。 以下是使用QuantumATK计算的自旋体光伏的电荷流和非共线自旋流性质,文中考虑了三种二维材料中的铁电调控情况,分别是面内铁电材料(BP-Bi为例): 面外铁电材料(α-GeTe为例): 和面内面外耦合的铁电材料(α-In2Se3): 总结: 该工作系统地提出了一个模型,用于描述自旋-光电旋效应(SPGE)在自旋轨道耦合(SOC)铁电半导体中的行为,考虑了一阶相对论扰动(Rashba效应),包括平面内、平面外和平面内-平面外耦合的自旋轨道耦合。在平面内铁电材料中,可以通过调节铁电性质来调制Sz分量的自旋电流,但不能通过圆偏振光来实现。在平面外铁电材料中,无论是线偏振光还是圆偏振光都可以通过调节铁电性质来调制Sx和Sy分量的自旋电流。在耦合铁电材料中,无论入射光的类型如何,都可以通过铁电性质有效地控制自旋电流的所有三个分量。通过采用第一性原理计算和量子输运,该文使用BP-Bi、α-GeTe和α-In2Se3这三个案例验证了这个模型。结果表明,当忽略高阶相对论扰动时,该模型是成立的。然而,当铁电材料受到来自高阶相对论效应(Dresselhaus效应)的扰动时,需要对模型进行特定修改。这项工作为未来关于电-光-磁耦合新型存储器的研究铺平了道路。 参考文献: Tunable spin photogalvanic effect in two-dimensional van der Waals ferroelectric semiconductors with spin-orbit coupling. Phys. Rev. B 109, 195202 (2024); DOI:https://doi.org/10.1103/PhysRevB.109.195202
基于Janus-MoSSe和C3N4构建的范德华异质结中的可调节能带排列和光学特性
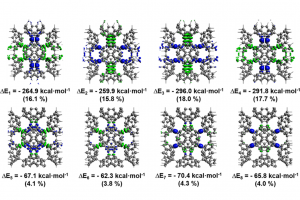
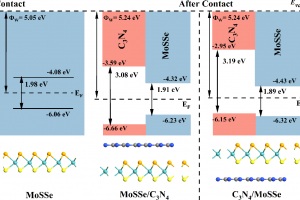
背景简介 具有可调节能带排列的范德华异质结被认为是未来制造高性能多功能纳米光电器件的理想候选材料。在半导体与半导体结合构建的异质结构中具有多种能带排列方式,包括I型(跨接)、II 型(交错)以及 III 型(断隙)。I 型异质结构中的电子和空穴都位于同一种半导体材料中,这将有利于载流子的快速复合,这一特性使得I型异质结通常用于发光器件中。而在II型异质结构中,电子和空穴则位于不同的半导体材料,这种空间上的分离能够有效抑制载流子的复合并延长层间激子寿命,因而在太阳能器件中得到广泛应用。对于III型异质结构,由于两种半导体材料的价带和导带相互重叠,导致III型异质结构具有更高的电子隧穿概率。因此,实现异质结构的可调节能带排列是制造高性能的多功能纳米光电器件的前提。然而,目前大多采用调节异质结构的构成层成分或者厚度的方法来实现能带排列方式的变化,显然这些方法难以在实验中实现。 研究内容 由于具有 S 原子和 Se 原子两个不同的表面,因此 Janus-MoSSe 两表面的电势并不相同。基于 MoSSe 的这种特性并考虑 C3N4 相对 MoSSe 的不同旋转角度,通过结合能的计算获得最稳定的 MoSSe/C3N4(C3N4-Se)和 C3N4/MoSSe(C3N4-S)异质结构,并进行相关性质的研究。研究表明,由于两种异质结构内建电场强度的不同(图1c-d)导致构成层的能带边缘位移的差异(图2),MoSSe/C3N4 异质结构呈现出I型能带排列特征,这将适用于发光器件中,C3N4/MoSSe 异质结构呈现出II型能带排列特征,这将有利于载流子的分离并在太阳能器件中具有较大应用潜力。相较于目前调控异质结构能带排列方式的手段,这种通过切换异质结构堆叠方式来实现的方法,将更容易在实验中实现。此外,这两种异质结构的能带排列方式可以通过外加电场进行调节,即在I型和II型能带排列之间转换。另一方面,两种异质结构在原始状态下的主要吸收峰都位于可见光区(~2.9eV),通过施加正(负)方向电场,吸收峰的峰值可以得到增强(减弱),这一特征使得 MoSSe/C3N4 和 C3N4/MoSSe 异质结构可以应用于光调制器中。这些研究结果表明,MoSSe/C3N4 和 C3N4/MoSSe 异质结构在多功能电子器件(包括发光器件、太阳能器件、光调制器等)中具有巨大的应用潜力。 图1 MoSSe/C3N4 和 C3N4/MoSSe 异质结构的(a-b)层相关的投影电子能带结构和(c-d)沿z方向的有效势。 图2 MoSSe/C3N4 和 C3N4/MoSSe 异质结构的能带排列和功函数示意图。ΦW、Evac 和EF 分别表示功函数、真空能级和费米能级。真空能级设置为零。 总结 基于 Janus-MoSSe 的面外不对称性,将 C3N4 分别放置在MoSSe 的不同侧面构建出 MoSSe/C3N4(C3N4-Se)和 C3N4/MoSSe(C3N4-S)异质结构,以此希望通过更为简便的方法实现异质结构能带排列方式的转换和更强的光学性能。由于 MoSSe 两侧原子的势能差异,两种异质结构的内建电场强度并不相同,导致其构成层能带边缘的位移程度也存在差异,最终 MoSSe/C3N4 […]
阴离子与芳香五酰胺大环的结合与迁移(Nat. Chem. 2023)
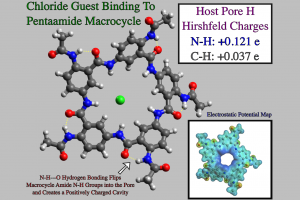
如果主体对携带特定电荷的客体物种具有亲和力,则可能用于对于对抗各种疾病。合成的超分子结构被设计为与阳离子或阴离子结合,利用官能团的影响得到大环的孔,以获得负电荷与阳离子相互作用,或正电荷以结合、运输阴离子。通过迫使孔隙带正电,让生物膜主体具有阴离子结合特异性,这对于对抗氯离子输送故障和治疗囊性纤维化非常重要。在最近的一项研究中,主体五酰胺大环被特异官能化,通过N-H–O氢键迫使酰胺基团被定向到孔中,如此将相当大的正电荷放入五酰胺的空腔中,并将羰基翻转到大环之外。由于孔中 NH 和 CH 的正电荷,这些五酰胺大环对阴离子具有特异亲和力。 五酰胺大环上的 Hirschfeld 电荷和静电势,以及单体构建块的偶极矩,使用 ADF 计算得到,证明了腔的强正电性。几何优化表明,过量阴离子客体被吸引到五酰胺大环的正电空腔中。计算的缔合常数和结合能表明,主体空腔偏向去溶剂化,以允许孔内容纳阴离子客体。本文特别关注了主体结构内氯化物、溴化物和碘化物客体的结构优化,计算表明碘化物与五酰胺腔的结合最强,其次是氯化物,溴化物的结合最弱。这与 N-H–Cl– 相互作用强于 N-H–Br– ,N-H–I– 相互作用最弱的一般趋势相反。结构优化表明,碘化物与五酰胺大环的结合最强,因为它的尺寸更大,能够与孔中的所有N-H基团相互作用。由于氯化物和溴化物的尺寸较小,这两种阴离子只能聚集两个 N-H 基团配位。考虑到氯化物比溴化物的结合力强,又不像碘化物那样过度填充孔隙,因此相对于其他卤化物,氯化物的传输能力最好。 因此,正如ADF计算结果所显示的那样,五酰胺大环是对抗囊性纤维化和补充氯化物正常运输的理想选择。 参考文献 Ruikai Cao, Robert B. Rossdeutcher, Yulong Zhong, Yi Shen, Daniel P. Miller, Thomas A. Sobiech, Xiangxiang Wu, Laura Sánchez Buitrago, Karishma Ramcharam, Mark I. Gutay, Miriam Frankenthal Figueira, Pia Luthra, Eva Zurek, Thomas Szyperski, Brian Button, […]
ReaxFF新力场:全无机卤化物钙钛矿中卤化物混合的原子效应
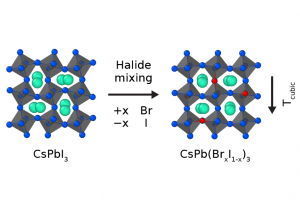
摘要 金属卤化物钙钛矿已成为光电应用中极具前景的材料,其卓越的性能使其成为太阳能电池和LED的理想候选材料。现有的钙钛矿组合物通常涉及不同离子的混合,目的是针对特定应用,对材料的光电性质和稳定性进行微调。为了理解离子混合的原子效应,埃因霍温理工大学和宾夕法尼亚州立大学的研究人员开发了一种用于大规模分子动力学模拟的无机金属卤化物钙钛矿(CsPbX3,X=Br 或 I)的 ReaxFF 力场[1]。 研究人员利用 DFT 计算生成的参考数据集,使用 AMS 软件中的 ParAMS 参数化功能,基于先前开发的 CsPbI3 的力场(该力场有助于研究体材料降解反应[2]以及表面和晶界的影响[3]),对该力场进行了扩展, 得到了新的无机卤化物钙钛矿的 ReaxFF 力场[4] CsPb(BrxI1-x)3 ,新开发的 I/Br/Pb/Cs 参数集首次对 Br 进行描述。在包括状态方程、混合焓、降解反应和缺陷迁移能垒在内的各种基准测试中,该力场表现良好。在分子动力学模拟中,该力场可以准确地再现材料的有限温度效应,例如无机钙钛矿的各种体相之间的相变。 使用新的力场参数,研究人员确定,由于 I 和 Br 离子的尺寸失配,卤化物混合对材料中八面体的相变温度和倾斜动力学有着深远的影响。利用卤化物混合的稀释极限(即取代钙钛矿晶格中的单个卤化物),确保这种效应是非局部的,距离混合位点高达两纳米。混合效应的非局部性,解释了为什么少量卤化物混合会对材料性质(如相变温度)产生很大影响。新的 ReaxFF 力场参数,为大型现实体系通过原子模拟,进一步探索无机混合卤化物钙钛矿的复杂动力学铺平了道路。 参考文献 Pols, M.; van Duin, A. C. T.; Calero, S.; Tao, S. Mixing I and Br in Inorganic Perovskites: Atomistic Insights from Reactive Molecular […]