摘要
本文介绍了用第一性原理计算模拟方法研究了$\mathrm{X}_3 \mathrm{P}_2$($\mathrm{X}=\mathrm{Mg,Ca}$)的结构、力学和光电性能的工作。结构和力学性能的结果表明,$\mathrm{X}_3 \mathrm{P}_2$ 化合物具有热力学和力学稳定性。此外,弹性常数和体积模量结果表明,$\mathrm{Mg}_3 \mathrm{P}_2$具有韧性,$\mathrm{Ca}_3 \mathrm{P}_2$为脆性。对能带的计算结果表明,两个化合物($\mathrm{Mg}_3 \mathrm{P}_2$ 和 $\mathrm{Ca}_3 \mathrm{P}_2$)的直接带隙($\Gamma – \Gamma$)分别为 0.523 eV 和 0.446 eV(GGA 泛函)。然而,在使用 HSE06 杂化泛函时,$\mathrm{Mg}_3 \mathrm{P}_2$ 的带隙提高到1.282 eV,$\mathrm{Ca}_3 \mathrm{P}_2$ 则提高到 1.092 eV。这两种化合物在可见光区域都表现出高光学吸收($\geq 10^5 \mathrm{cm}^{−1}$) 使其成为光伏应用的潜在候选材料。
结构和力学性质
两种材料的结构如下图:
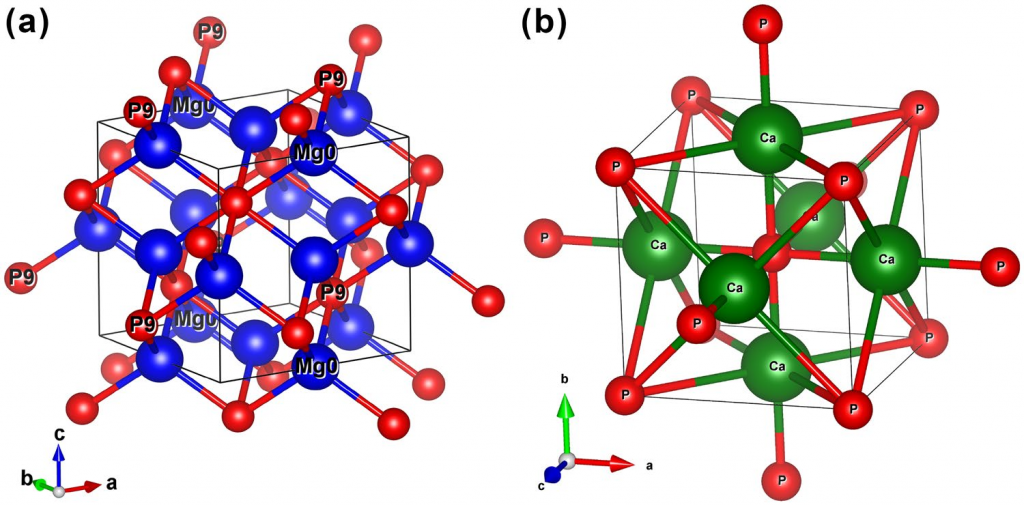
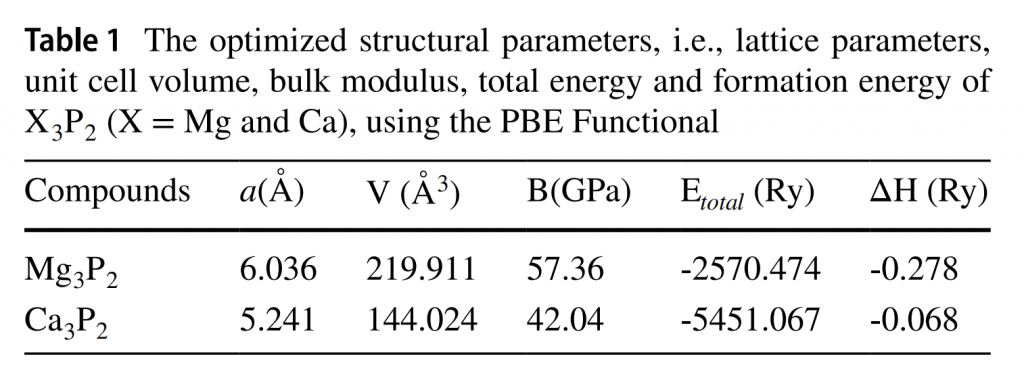
结构经过优化后,对它们计算形成能(焓),即与稳定单质相比的能量:$$\Delta H (X_3 P_2) = E_{total} – 3E_{total}(X) – 2E_{total}(P)$$ 结果表明两个化合物都具有热力学稳定性。
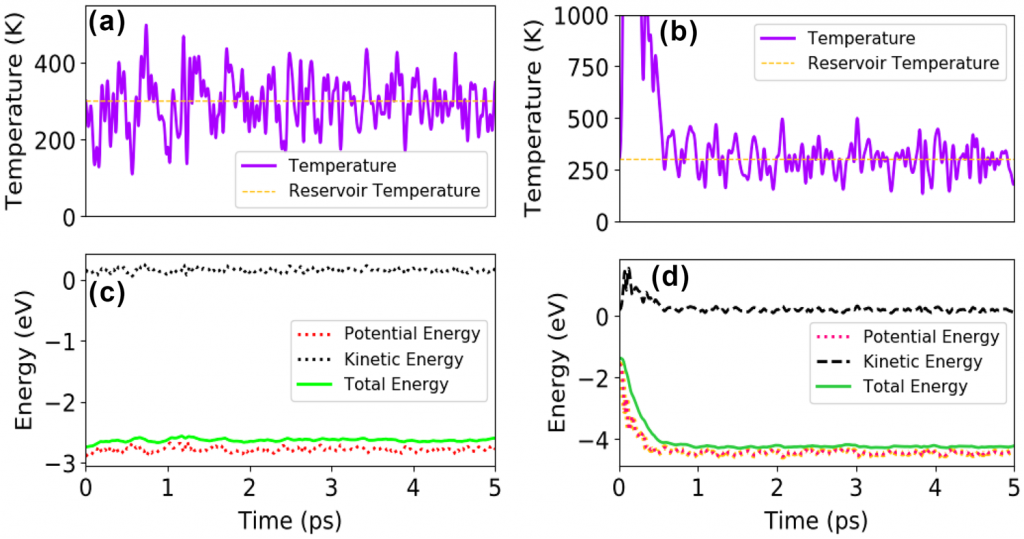
为了进一步验证结构的稳定性,作者进行了分子动力学模拟,证实了在分子动力学水平上在室温下结构的动态稳定性。
作者还计算了体系的弹性系数矩阵,进行了Born-Huang晶格力学稳定性分析。由弹性系数矩阵可以得到体系的体模量、剪切模量、杨氏模量、泊松比、Pugh ratio等多种力学性质,并据此可以评估材料的延展性和脆性。

电子态和光学性质
使用PBE密度泛函和HSE06杂化泛函计算了体系的能带、态密度与投影:
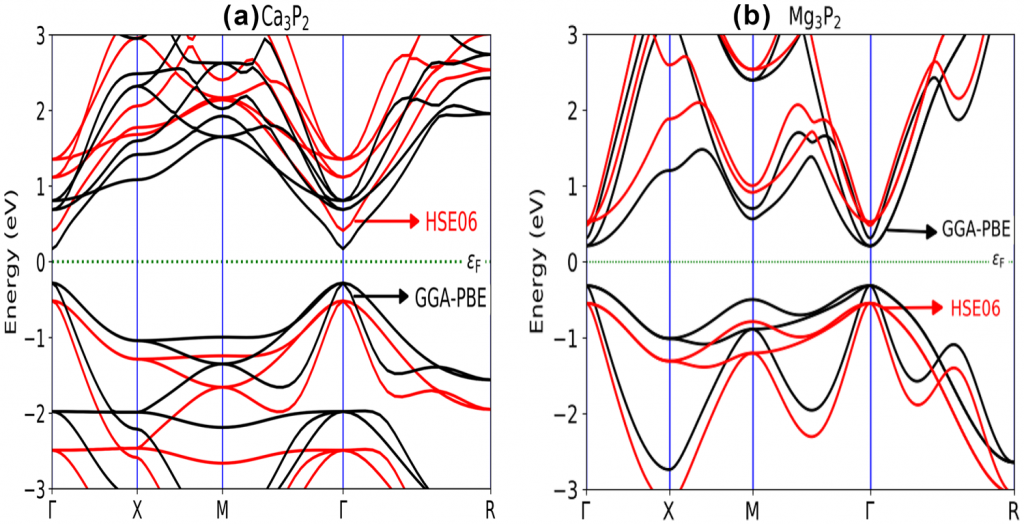
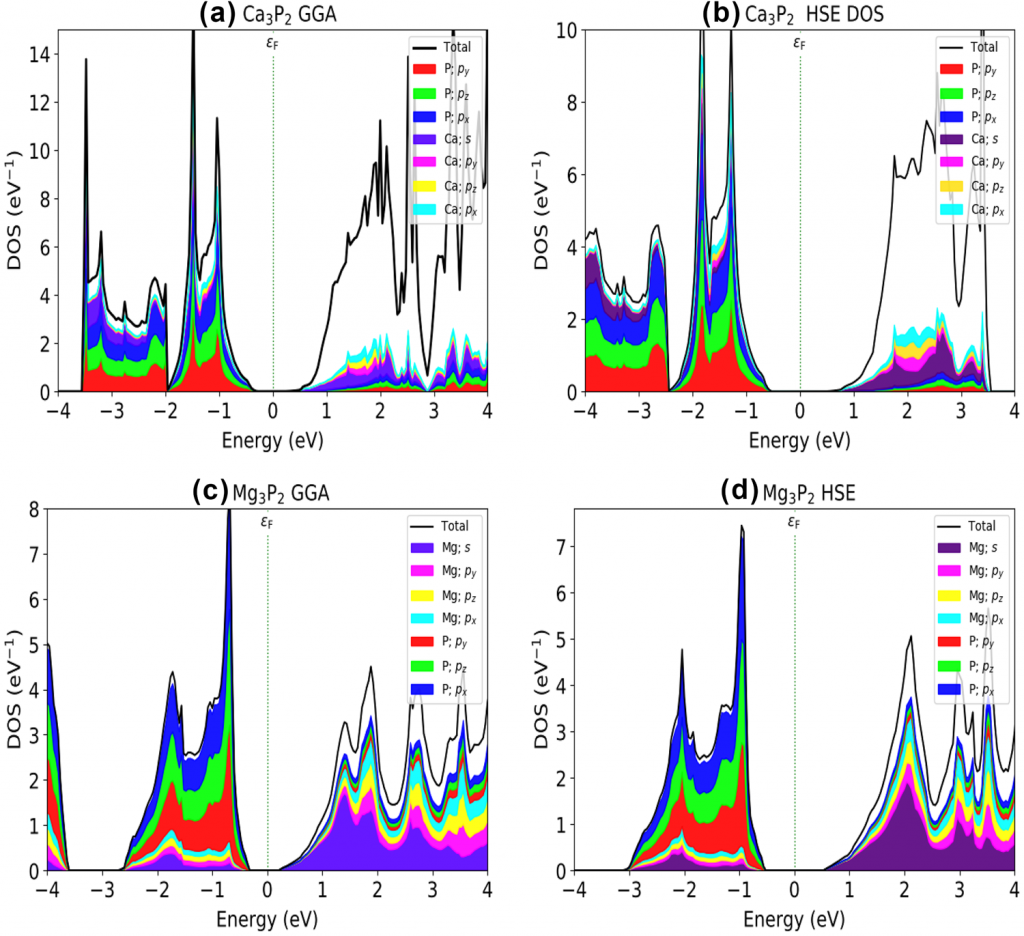
使用HSE06对两种材料的光谱进行了计算:
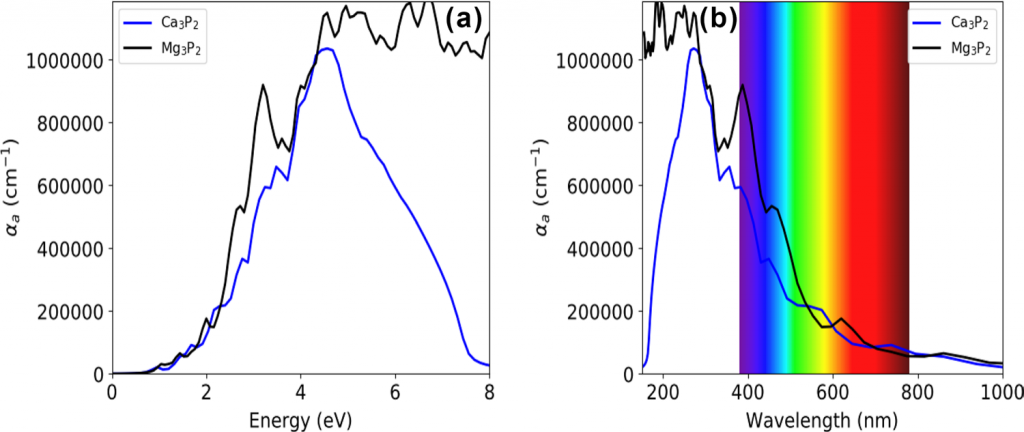
参考
- Bougherara, K., Al-Qaisi, S., Laref, A. et al. Ab initio Insight of the Electronic, Structural, Mechanical and Optical Properties of X3P2 (X= Mg, Ca) from GGA and Hybrid Functional (HSE06). J Supercond Nov Magn 35, 79–86 (2022). https://doi.org/10.1007/s10948-021-06009-3
