微孔结构中速度和压力分布的孔隙级 CFD 研究

Posted · Add Comment

概述

多孔金属结构具有独特的高孔隙体积、高表面积和高杨氏模量的组合特性，广泛应用在与流体、热、压力波和机械冲击相互作用的材料中，适合作为各种工程和工业应用中的承重结构。典型的应用领域包含二氧化碳捕集和能量储存、过滤和减少废物、吸声、生物医学设备、能源（石油和天然气）和冶金加工。其他应用还包括如热交换器和吸声器的材料、水泥窑中的交换介质以及稠油和蒸汽辅助重力泄油（SAGD）技术中的下一代筛管材料。

本项目提出了一种基于微观尺度层析成像数据的孔隙结构表征和计算流体动力学（CFD）的建模方法，并模拟了流体在“真实”和“自适应”多孔金属结构中的流动分布。深入理解流体从达西到惯性的流动形态，并证实孔隙结构相关参数与多孔介质流体流动特性的关系。

亮点

  • 在 Simpleware ScanIP 重建真实结构、创建“自适应”结构、表征孔隙；
  • 在 Simpleware FE 生成高质量的网格模型；
  • 在 Simpleware FLOW 模拟多孔介质流体流动特性，研究其与孔隙结构相关参数的关系。

图像获取

使用蔡司 Xradia Versa XRM-500 三维 x 射线 CT 显微镜获取高多孔金属样品的断层扫描数据集，材料为 Inconel 450 μm、Inconel 1200 μm、Recemat RCM-NCX 1723、Recemat RCM-NCX 1116 和 Porvair 7PPI 泡沫。

在 Simpleware ScanIP 中将 2D 灰度层析成像数据集渲染成 3D 结构，从大型样品中心截取一个 6-12 倍于结构平均孔径的长方体代表性体积单元（RVE）。阈值大小也会对微观结构的拓扑及宏观参数产生影响，处理后的 3D 代表性体积与完整样品的孔隙率最小偏差仅为 ±2 %。

图1：通过 CT 扫描重建 Inconel 450 μm图像（a）多孔样品（b） Xradia-500 显微镜（c）高分辨率 2D CT 切片数据（d）图像渲染和阈值处理（e）三维重构多孔样品（f）代表性体积单元的骨架相（g）内部孔隙表征（h）孔隙开孔（i）多孔基质的支柱或纽带以及分割后的（j）3D 和（k）2D 孔隙。

图像处理

在 Simpleware ScanIP 中：

  • 直接测量代表性结构的孔隙率、孔隙体积、骨架体积、骨架表面积等结构参数。
  • 通过布尔运算和分水岭算法获得孔隙结构（流体域），创建一条穿过结构开口和孔隙的中心线以确定平均孔径大小。
  • 利用腐蚀和膨胀工具创建“半虚拟”即“自适应”结构。

模拟

在 Simpleware FE 模块对代表性 Inconel 450 μm 的多孔结构进行网格划分，生成高质量的线性四面体网格（LTM）。采用不同边缘长度的 LTM 网格和高密度的六面体/二次四面体混合网格（HQTM）模型在 Simpleware FLOW 模块计算压降，并对结果进行比较。这样对于有效解决足够大小微尺度模拟结果产生宏观尺度系统可接受度很有必要。

HQTM 网格结构的高自由度（3D RVE Inconel 450 μm样品的网格密度接近 3 千万个单元）需要高内存和使用较长的计算时间，因此在商业 CFD 软件中的求解计算要求很高。大多数商业 CFD 软件使用 Taylor-Hood P2-P1 单元（速度的二次元和压力的线性元）进行计算。 Simpleware FLOW 的求解器在流体流动计算中默认使用稳定的 P1-P1 单元（速度和压力计算都是线性的），减少了未知数的量，使计算速度更快、占用内存更少。

图2：结构网格密度（单元数）与压降比的关系图。

结果

通常，流体在多孔介质上的输运可以用方程 Darcy 模型描述，将多孔结构上形成的单位压降（∇P）表示为表层流体速度（νs）的函数。该方程还发展为解释填充层中水流的导水率和渗透率，适用于非常缓慢的流体即孔径雷诺数（RED）小于 1 的体系。Phillipe Forchheimer 又进一步解释了多孔介质中高流速和极高流速下的惯性效应，有助于计算多孔金属中流体流动的两个最重要参数（渗透率 k0 和形状阻力 C），这些参数随孔隙大小、孔隙开孔、间隙和孔隙形态的不同而变化。

通过 RCM-NCX 1723 多孔样品的二维图可以很容易解释流体在“真实”和“自适应”结构中的流动模式及表现形式。图（c）在较高的孔径 RED （湍流）下，多孔基质内的流体流动主要表现为流体颗粒在结构间隙内的快速运动。这就证实了湍流的发生不仅需要高的流体速度，还以不稳定涡流的形成为特征。图（e）腐蚀后多孔结构骨架的孔隙体积增加，减少了流动涡流（回流效应），使材料内部形成稳定的流线流动。相反地，图（d）膨胀后结构中不稳定的流体流动模式增加了运动流体与孔壁间的耗散能和阻力形成。

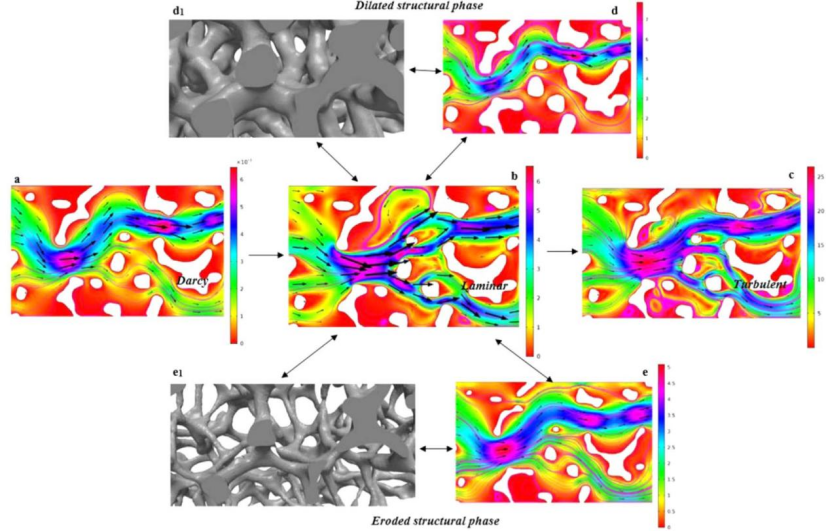
图3：RCM-NCX 1723 多孔金属内流体流动的速度流线/箭头的 2D 等轴视图（a）达西表层流体流动速度为 1.0 × 10-3 m.s-1（RED= 0.123）（b）层流区表层流体流动速度为 1.0 m.s-1（RED= 123）（c）湍流区表层流体流体流动速度为 5.0 m.s-1（RED= 407）（d）膨胀结构相在层流区表层流体流动速度 1.0 m.s-1（RED= 123）（e）腐蚀结构相在层流区表层流体流动速度 1.0 m.s-1（RED= 123）

随着孔隙体积的减小，惯性开始降低，膨胀结构的过渡状态逐渐缩短。过渡 RED 的减小趋势可能是由于膨胀多孔结构的高表面粗糙度和拓扑结构所致。

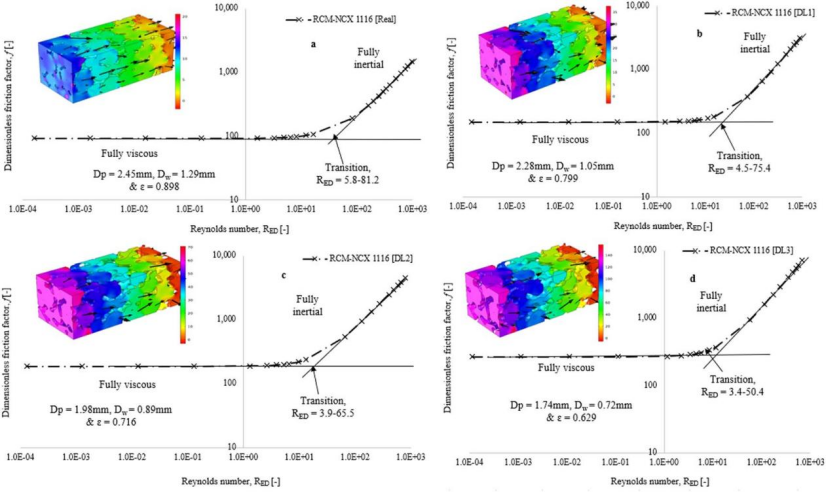
图4：表层流体入口速度为 1.0 m.s-1 时计算的 3D 压力流线/箭头图和无量纲达西摩擦系数 f 与基于孔径的雷诺数 RED 的对数关系图（a）真实结构（b）膨胀 1 个像素（c）膨胀 2 个像素（d）膨胀 3 个像素

高多孔的开孔结构具有高孔隙体积分数（0.72 以上）、高渗透率和低形状阻力的特点。相反，闭孔结构的孔隙体积分数低（0.66 以下）、渗透率低、形状阻力大。通过与文献中可用实验测量数据进行比较，证实这种孔隙尺度 CFD 计算方法中建模的置信度。

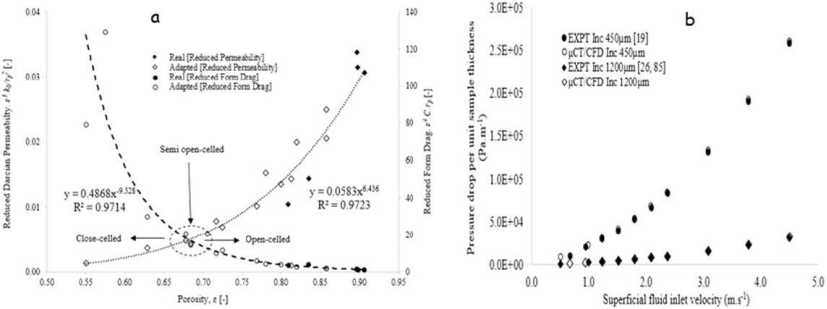
图5：（a）减少的达西渗透率和减少的 Forchheimer 形状阻力与孔隙率的关系（b）实验与 CFD 模拟的单位压降与表层流体入口速率的关系

结论

本研究提供了一种通过孔隙图像数据理解多孔金属结构中速度与压力分布的方法，从而确定孔隙结构参数与流体流动性能的关系，得出以下结论：

  • 微观结构的优先开孔主要决定了流体通过其间隙的运动，特别是以弱振荡和流线型流体运动为特征的缓慢流体。而流体运动和基质孔壁之间的再循环、混沌运动和增加的阻力主导了快速流动的流体。
  • 将流体流动规律应用于 CFD 预测压力和表层流体速度的对比，证实了微孔结构中的流体流动从达西到惯性的表现形式。
  • 膨胀结构降低了孔隙体积和孔隙开口，引起高压积聚和更加混乱的流体运动，从而导致在减小的雷诺数下形成了湍流。
  • 这种方法有助于理解可能难以通过实验表征的狭窄通道内流体流动的分布。

参考

  • Otaru A J, Samuel M B. Pore-level CFD investigation of velocity and pressure dispositions in microcellular structures[J]. Materials Research Express, 2021, 8（4）: 046516.