采用基于 μCT 的有限元分析评估木材的导热系数

概述

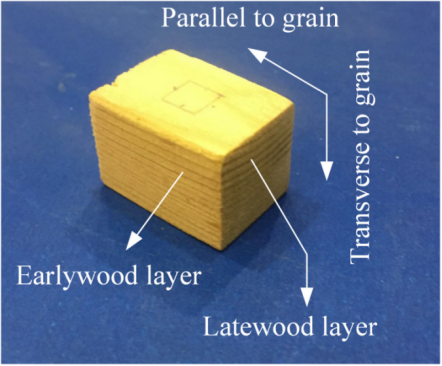
木材是一种来自树木或木质植物的天然物质，在建筑、燃料、器皿、乐器和其他复合材料行业都有广泛应用。在燃料领域，木材也成为探索新型电极材料的关注点。木质纤维素和多通道微观结构有助于钒液流电池充电中离子导电型电解质的传质。无论是实验还是设计工作，研究控制介质传递热量内在能力的导热系数都具有非常重要的实际意义。

本项目提出一种结合 X 射线显微计算机断层扫描（μCT）和有限元分析（FEA）在介观尺度测试木材导热系数的方法。通过对具有两相成分（早材和晚材）的真实木材进行三维重建，研究纹理、孔隙率和水饱和度对木材导热性能的影响。

图像处理

本研究所用为松树锯材，纹理层是深/亮黄色交替的图案。纹理表示树木不同季节形成层活动下细胞纤维的取向，可分为早材和晚材。早材层源自薄壁木质细胞，呈现出明显较浅的颜色和较宽的线条图案。晚材呈现为较暗的线条图案，通常在夏季生长更密集且细胞壁含量更高。木材形成的纹理使其具有各向异性的材料特性。采用 μCT 在介观尺度获得木材试样的内部几何结构，尺寸为 15 × 15 × 20 mm。

考虑到计算资源和耗时，从三个不同位置裁剪 4 × 4 × 4 mm的感兴趣区域（ROI）作为模拟和分析的计算模型。对三个 ROI 的模拟结果进行平均得到具有统计代表性的均匀场，考虑到了整个木材纹理密度的异质因素。

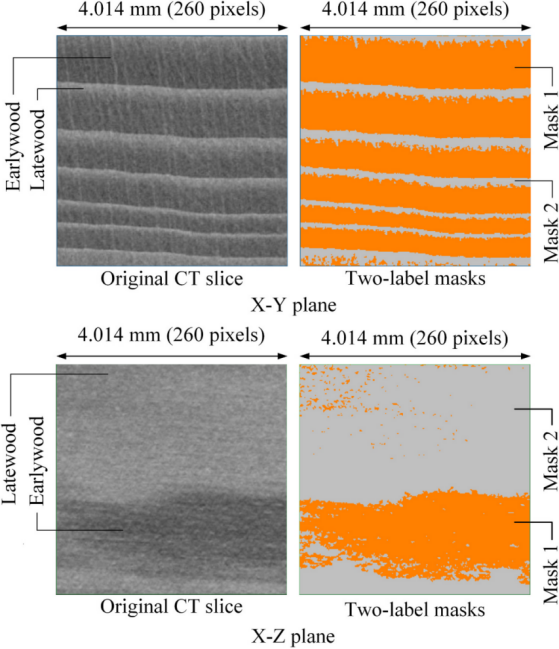
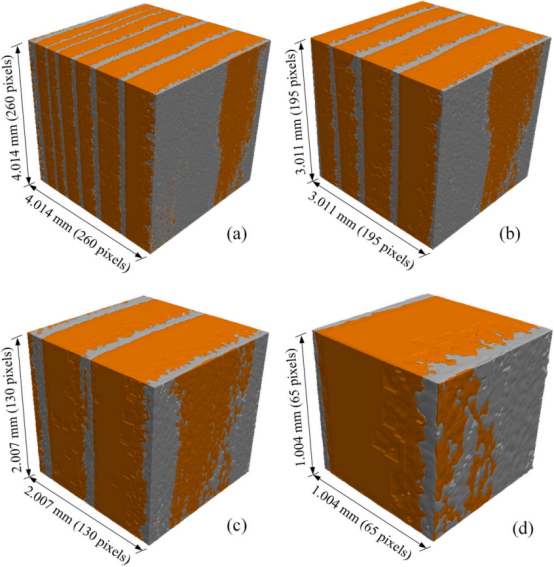
为了解尺寸对热传导模拟可靠性的影响，将 ROI 裁剪为体积从 1 mm³ 到 64 mm³ 的立方体模型。试样编号如 W4-T-0.8-0.6，W 表示木材；4 为模型边长 4mm；T 表示木纤维的横向（P 表示平行于木纤维）；0.8 是早材孔隙率；0.6 是晚材孔隙率。

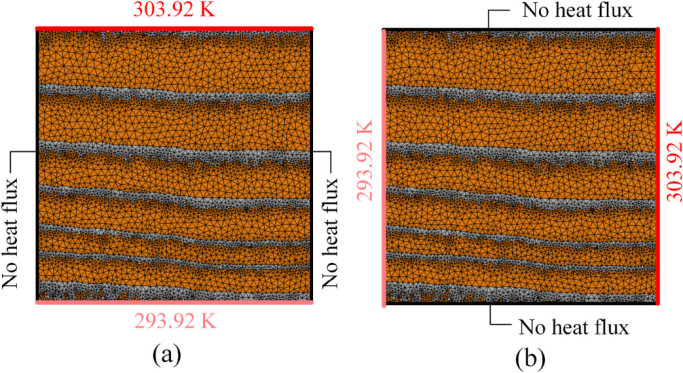
在 Simpleware FE 模块中采用 + FE Free 网格划分算法为分割后的结构生成高质量的四面体网格模型。为减轻相邻相间边界的几何不连续性，设置最大单元边缘长度为 0.1544 mm，目标最大误差为 0.001544 mm。

通过一维稳态热传导评估木材的导热系数，考虑了热流平行于纤维和热流沿纤维横向两种情况。将两个相对的表面分别设置为 303.92 K 和 293.92 K（初始温度），其余表面没有发生热通量。鉴于木材表面包含大量单元，在木材模型表面添加额外的掩膜作为储热层，以便轻松定义温度梯度。

结果和讨论

温度曲线

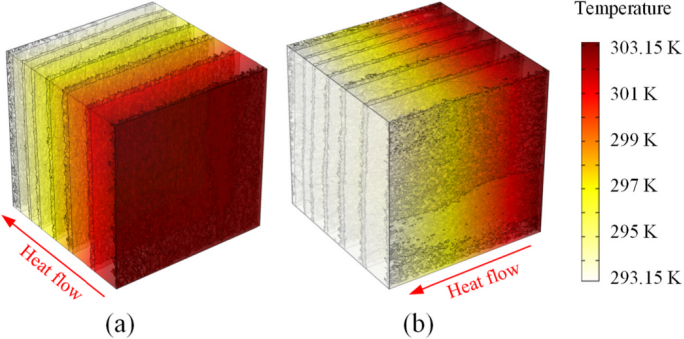
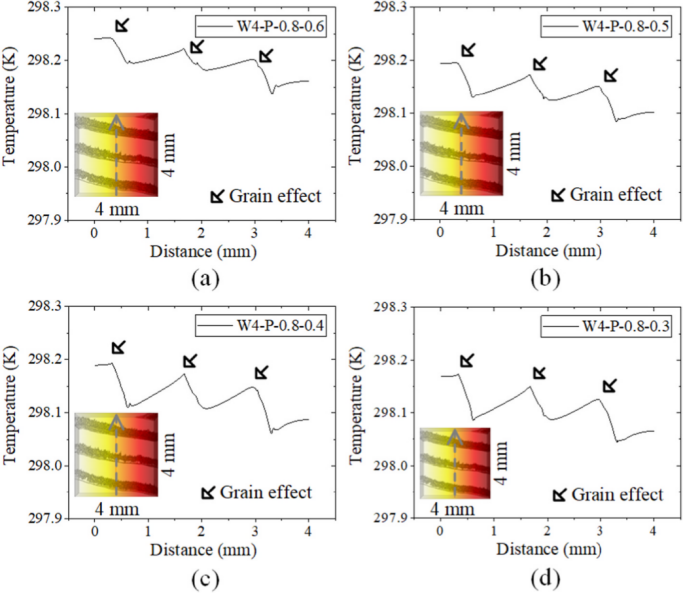
模拟产生的热流在两个方向（木纹横向和平行于木纹）穿过木质材料的空间分布如图所示。在稳态热流过程中，相互连接的木材层中形成温度梯度。

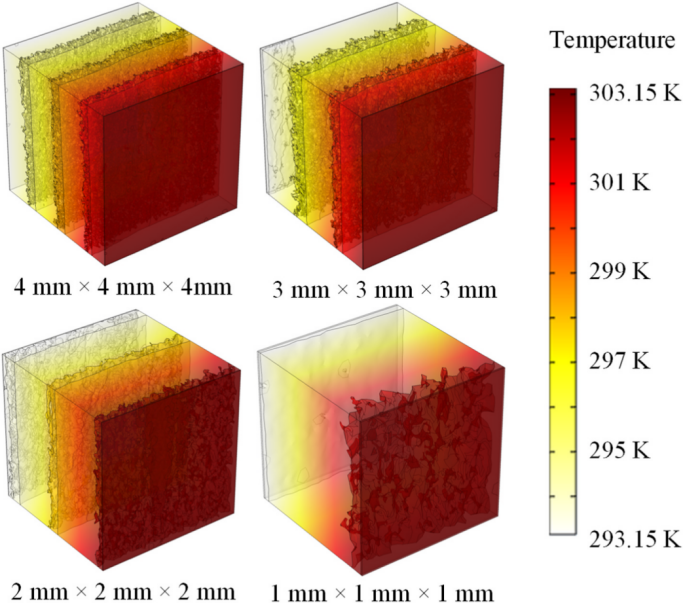
为评估模型尺寸的影响，构建四种不同尺寸的木材立方体模型。晚材层体积所占比例较小，但其形态结构却比早材层复杂得多。小的比例模型可能无法完全表征木纹对不均匀热传导的影响，从而导致模拟结果出现偏差。而增大木材模型的尺寸则会提高有限元求解器的计算成本，在 1 mm³–64 mm³ 的尺寸范围内自由度数量增加了几个数量级。

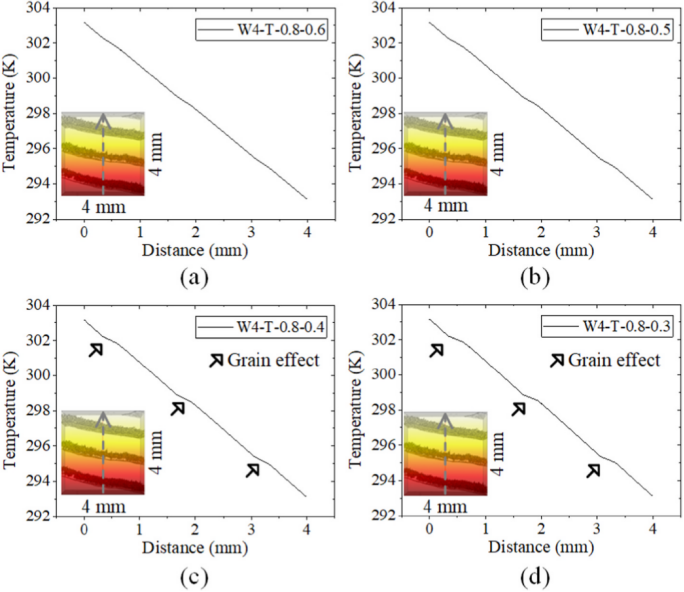
模拟记录了木材模型中心线的一维温度分布，可以探索纹理对热传导影响的机制。试样 W4-T-0.8-0.6 和 W4-T-0.8-0.5 的模拟结果显示温度随着热流距离的增加而降低。纹理对早材和晚材之间传热的影响不可察觉，然而对于 W4-T-0.8–0.4 和 W4-T-0.8–0.3，纹理的影响变得更加明显。晚材的孔隙率和相应的传导性与早材具有显著差异，导致试样中出现波状温度梯度路径。在平行热传导的情况下也发现了增强的纹理效应。

导热系数

除定性评估外，本研究还通过模拟中获得的稳态热通量以及温度梯度量化 3D 介观尺度木材模型的导热系数。基于 μCT 的有限元分析和理论模型计算得到的平均导热系数及相应偏差均接近。

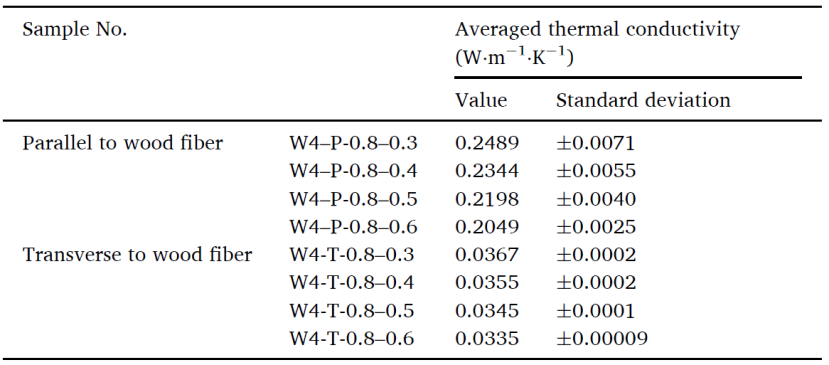
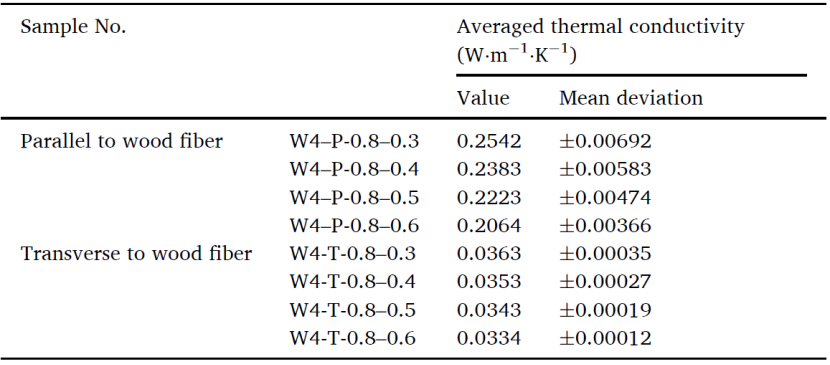
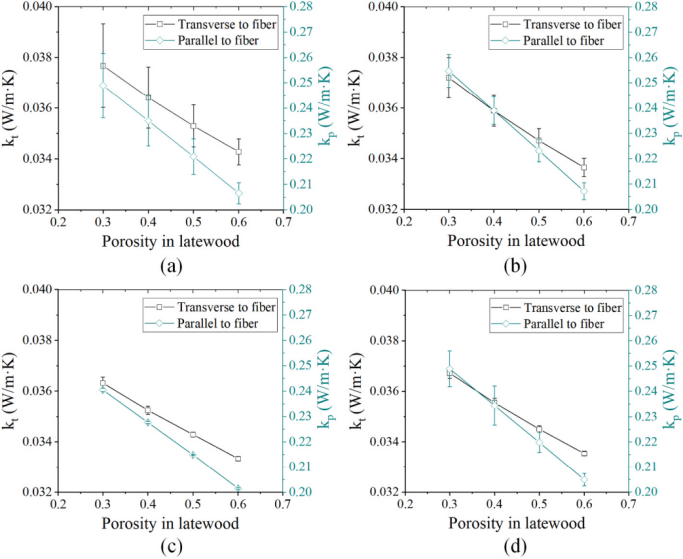
平均横向导热系数 k_t 和平行导热系数k_p 都随着晚材孔隙率的增加而降低。结果表明木纹对模拟热传导有显著影响，平行于木纹方向的导热系数是横向的 6 ~7 倍。此外，增加木材模型的尺寸会减少模拟导热系数的散射。

水分影响

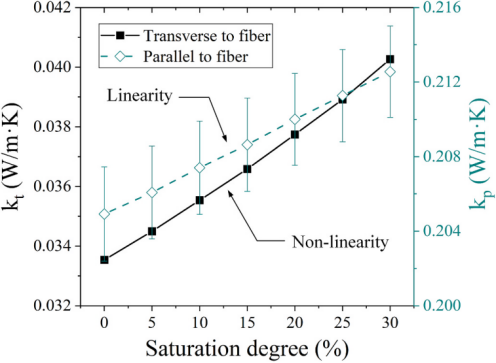
计算水饱和度分别为 0%、5%、10%、15%、20%、25% 和 30% 时的导热系数。当孔隙饱和度增加时，可明显观察到横向和平行导热系数均升高，但趋势不同。对于平行木纤维的热传导，导热系数随水饱和度呈线性增大。在木纤维横向上的一定水饱和度范围内，其与导热系数是非线性关系。结果表明，可能通过纹理方向和相对湿度的耦合作用设计具有特定传热行为的木制品。

总结

本研究提出一种基于 μCT 的有限元分析方法测量木材的导热系数。结果表明，通过 μCT 技术可以清晰地了解木材的微观结构，有效创建包含早材和晚材的 3D 数字化复合木材模型。模拟获得的导热系数与计算的理论值和实验结果均一致。与现有的测试和数值模拟方法相比，该方法在研究木材导热性能方面展现出数值“虚拟”测试、高分辨率建模、快速评估和良好再现性等优势。

• 平行于木纹方向的导热系数是横向的 6-7 倍。
• 木材细胞的较低孔隙率可以增加木材的有效导热性。
• 在较高的水饱和度下，平行导热系数呈线性增长，横向导热系数为非线性增长。

参考

• Qiu Q. Thermal conductivity assessment of wood using micro computed tomography based finite element analysis (μCT-based FEA)[J]. NDT & E International, 2023, 139: 102921.