概述
对纤维增强复合材料(FRC)进行基于 μCT 图像建模的有限元分析,可增强复杂材料在各种负载场景和环境下如何变形、损伤及失效的理解。为准确模拟 FRC 的性能,有限元网格必须明确表征典型微观结构的复杂性,包括波状和随机间隔的纤维、不规则形状的制造缺陷(如孔隙)、预先存在的损伤(如微裂纹)和周围基体。本研究提出了一种将 μCT 图像数据转换为高质量网格模型的方法,并进行双轴和单轴有限元模拟。

扫描和图像处理
在先进光源 X 射线 μCT 光束线下对井字格尼龙 66 降落伞织物进行原位双轴加载试验,扫描设置体素尺寸为 1.3 μm。重建图像堆栈为 3.3 × 3.3 × 2.8 mm,裁剪 0.57 × 0.55 × 0.21 mm 的感兴趣区域(ROI)用于研究。使用 Zeiss Versa-500 X 射线 μCT 3D 电子显微镜对单向 AS4/8552 碳/环氧树脂复合层压板进行扫描,体素尺寸为 0.46 μm。图像堆栈最终尺寸为 430.56 × 448.04 × 436.54 μm,分别裁剪 96.6 × 96.6 × 96.6 μm 和 46 × 46 × 23 μm 两个子体积,记为 ROI-1 和 ROI-2。
FRC 断层图像:使用可训练的 Weka 插件自动识别孔隙,利用算法检测单个纤维。根据纤维截面在切片中的质心位置和半径绘制纤维轮廓,为每根纤维分配各自独特的灰度像素强度,生成 FRC 微观结构的降阶图像。然后,通过上采样减少阶梯效应对纤维边缘的影响。
尼龙井字格织物图像:调整切片垂直于径向,移除纬向纤维改善径向纤维的检测,根据纤维位置和半径生成径向纤维的降阶分割图像。采用同样的方法生成纬向纤维的降阶图像,将两者合并后获得整个井格织物的图像。
网格划分和边界条件
将两种试样的降阶图像导入 Simpleware 软件进行处理,使用 Resample 工具执行上采样操作,使原来的一个像素由四个新的像素表示。基于灰度值将纤维、基质和孔隙分割为不同的掩膜,采用 Recursive Gaussian 滤波器平滑,各个方向的 sigma (pixels) 值均设置为 5。将平滑操作产生的空白区域填充为基质掩膜,确保纤维和基质间边界的连贯。在 Simpleware FE 模块为纤维和基质掩膜生成高质量的四面体网格模型。

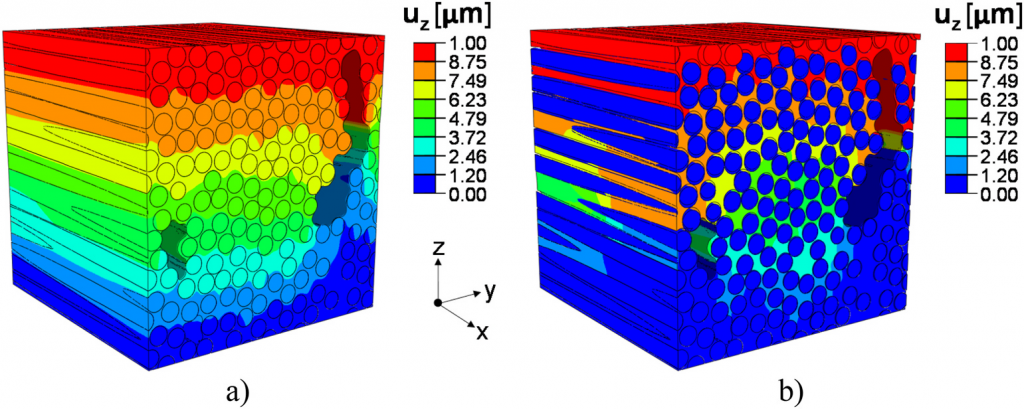
在 Simpleware 中,可以通过指定单元类型、网格质量指标和单元边长等控制生成的网格,还能够针对整个体积、每个掩膜或局部感兴趣区域调整单元边长。为展示不同的网格细化程度,使用三组不同的网格划分设置参数为 FRC ROI-2 生成网格。相较于 FRC ROI-2.1,FRC ROI-2.2 的纤维网格更粗糙,而 FRC ROI-2.3 的基质网格更粗糙。
将生成的网格模型导入 Abaqus 软件进行有限元分析。为简化模拟,假定所有相均为各向同性。对 FRC 微观结构沿 Z 方向施加单轴拉伸载荷,1 μm 位移使 ROI-1、ROI-2 产生的应变分别为 1% 和 2%。对尼龙井字格微观结构施加双轴拉伸载荷,14.25 μm 位移使 x 和 y 方向均产生约 5% 的应变。

结果与讨论
双轴拉伸模拟
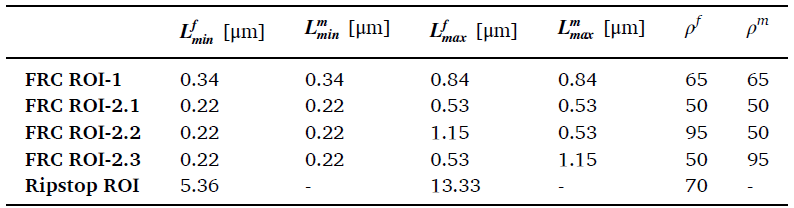
尼龙井字格织物的网格模型中包含 157 万个线性四面体单元,在配备 Intel Xeon E5-2690v4、2.6 GHz CPU、256 GB 内存的工作站使用 14 个并行内核耗时 226.9 分钟完成模拟。相邻纤维上的位移不均匀且不连续,表明纤维间彼此完全断开。X 方向取向的纤维在 Y 方向产生位移,反之亦然,表明彼此垂直取向的纤维通过摩擦接触力相互作用。纤维在 Z 方向上的位移表明由于施加的载荷而趋于伸直,因径向和纬向纤维间的正常接触保持波浪形。接触力在所有接触纤维间产生,但较高的法向和切向接触力主要在径向和纬向纤维之间。

单轴拉伸模拟
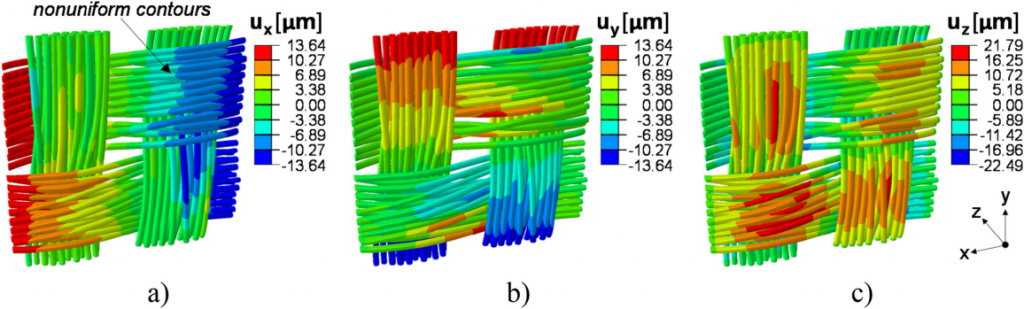
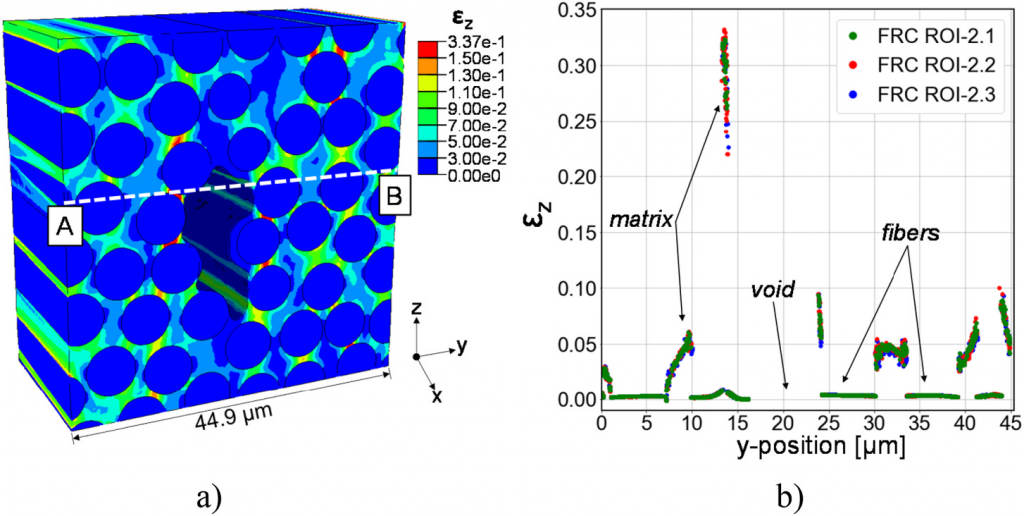
FRC ROI-1 的网格模型中包含 1830 万个线性四面体单元,采用同样的工作站配置,启用和禁用绑定约束两种情况分别耗时 206.2 和 96.7 分钟完成模拟。启用绑定约束时,离大孔隙较远区域的位移相对均匀,实现纤维和周围基质间适当的载荷传递。Y 方向的小波动可归因于两者刚度的局部不匹配,X 方向是因为纤维相对较直,Z 方向位移几乎没有变化。正如预期,位移会受到孔隙存在的干扰。禁用绑定约束时,纤维与基质断开,因此 Z 方向位移为零。
网格细化的影响
为比较不同网格划分参数生成的网格模型,统计其单元总数、纤维单元百分比和单元纵横比(AR)大于 3 的占比。AR 的可接受范围在 1 到 3 之间,1 对应于正四面体,每个网格模型中约 94% 的单元都满足,FRC ROI-2.1 获得最佳单元质量。

3 的占比
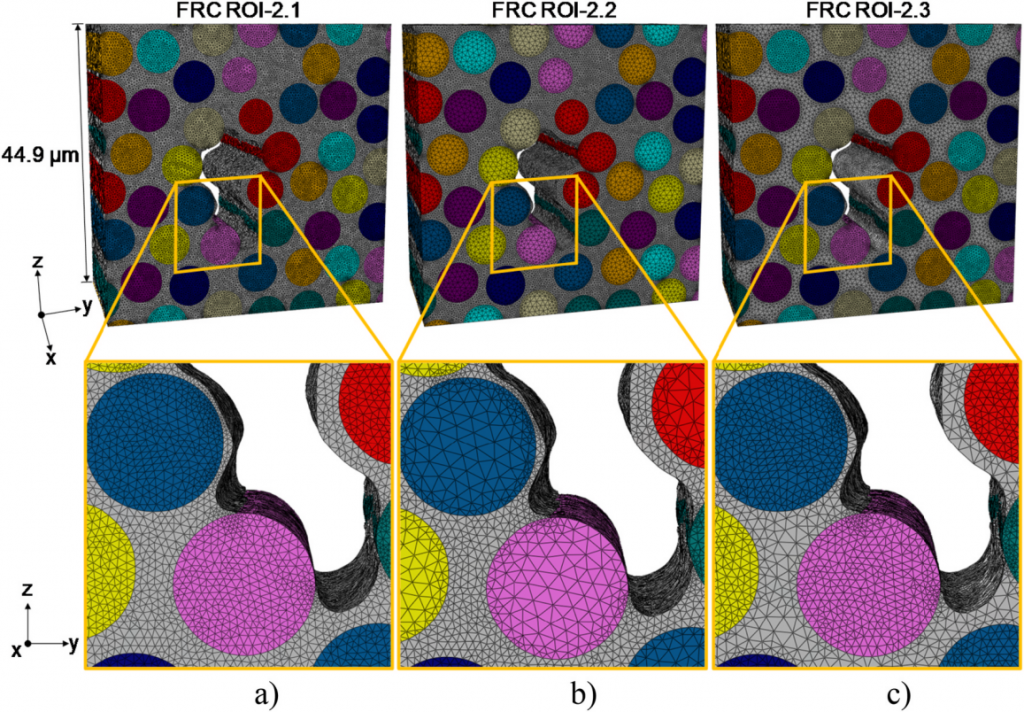
使用三个不同网格精细程度模型进行模拟获得的应变场间几乎没有差异,选择的目标单元边长和质量指标都确保生成了足够数量的单元,可以准确解析所考虑载荷情况下的微尺度应变。后续可采用更多不同参数研究网格收敛问题,确定最佳组合,在保证模拟精确度的同时降低计算成本。
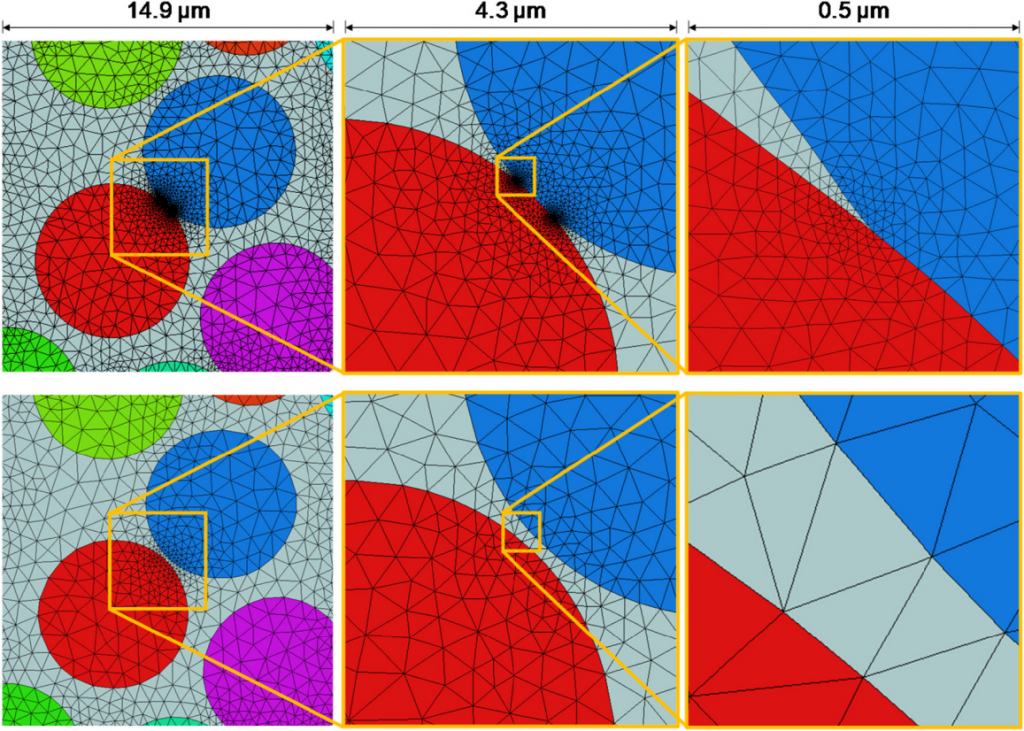
相邻纤维间的接触离散化
在生成 FRC 网格时,移除了相邻纤维间的相接表面,防止在相邻纤维和基体间形成大量且可能具有高纵横比的单元。对 FRC ROI-1 子体积中纤维间是否有相接表面情况生成的网格进行比较。准确表征两个接触纤维的几何形状将生成更多单元,约增加 15 倍。仍需更多实验研究确定浸润纤维间接触的物理可能性(如纤维浸润剂)及如何从数值角度模拟这种相互作用。
结论
本研究提出了一种基于图像的网格生成方法,将单向纤维增强复合材料和尼龙织物的 μCT 图像数据转换为网格模型,并进行有限元模拟和分析。
- 在微观尺度上实现织物和 FRC 的离散化,可单独赋予材料属性。
- 准确表征几何形状的前提下,成分(纤维或基质)内的单元粗糙化对计算的应变场几乎无影响。
- 为提高生成网格的质量,首先必须提高图像分割的精度。
参考
- Creveling P J, Fisher J, Dahlkamp C, et al. Modeling as-manufactured fiber-reinforced microstructures based on X-ray microcomputed tomography[J]. Composites Science and Technology, 2021, 214: 109004.
