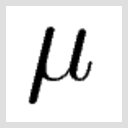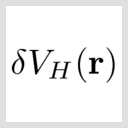格林函数方法模拟材料表面
本教程介绍如何使用一种非常新的方法计算表面性质:基于格林函数的表面计算。与传统的表面片层(slab)模型不同,表面电子态结构通过非平衡态格林函数(NEGF)方法与块体电子态耦合。
这里研究的是银(100)表面的功函数,主要介绍:
- 构建表面的结构;
- 设置并运行表面的格林函数计算;
- 分析功函数并与传统slab模型计算对比。
表面的原子模型
首先简单介绍基于格林函数的表面计算,以及与传统slab模型的不同之处。下面两幅图显示了这二者的不同。
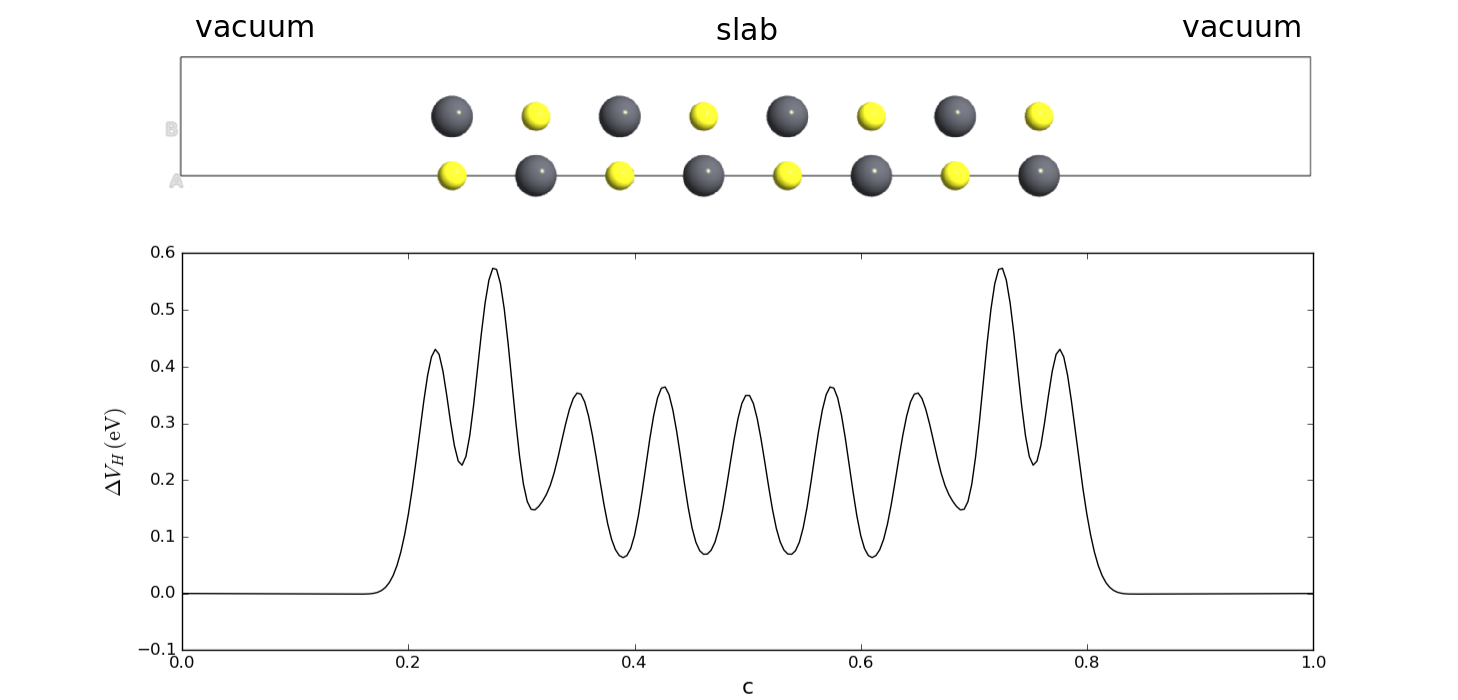
slab模型由有限层数的原子构成,C方向两边其他地方是真空,因此这个体系有两个表面(表面-真空界面)。静电(Hartree)势($V_H$)在slab的中间是和块体材料接近的,而在表面处有一定变化,并过渡到真空区域的常数。
与之不同,格林函数表面模型包含一个表面区域,并将其连接在一个电极上,电极部分是一个完整的块体材料周期结构。电子态在电极–表面区域之间的界面上通过格林函数匹配。因此,表面的电子态与块体基底连接,表面的化学势因此被固定为电极的化学势。
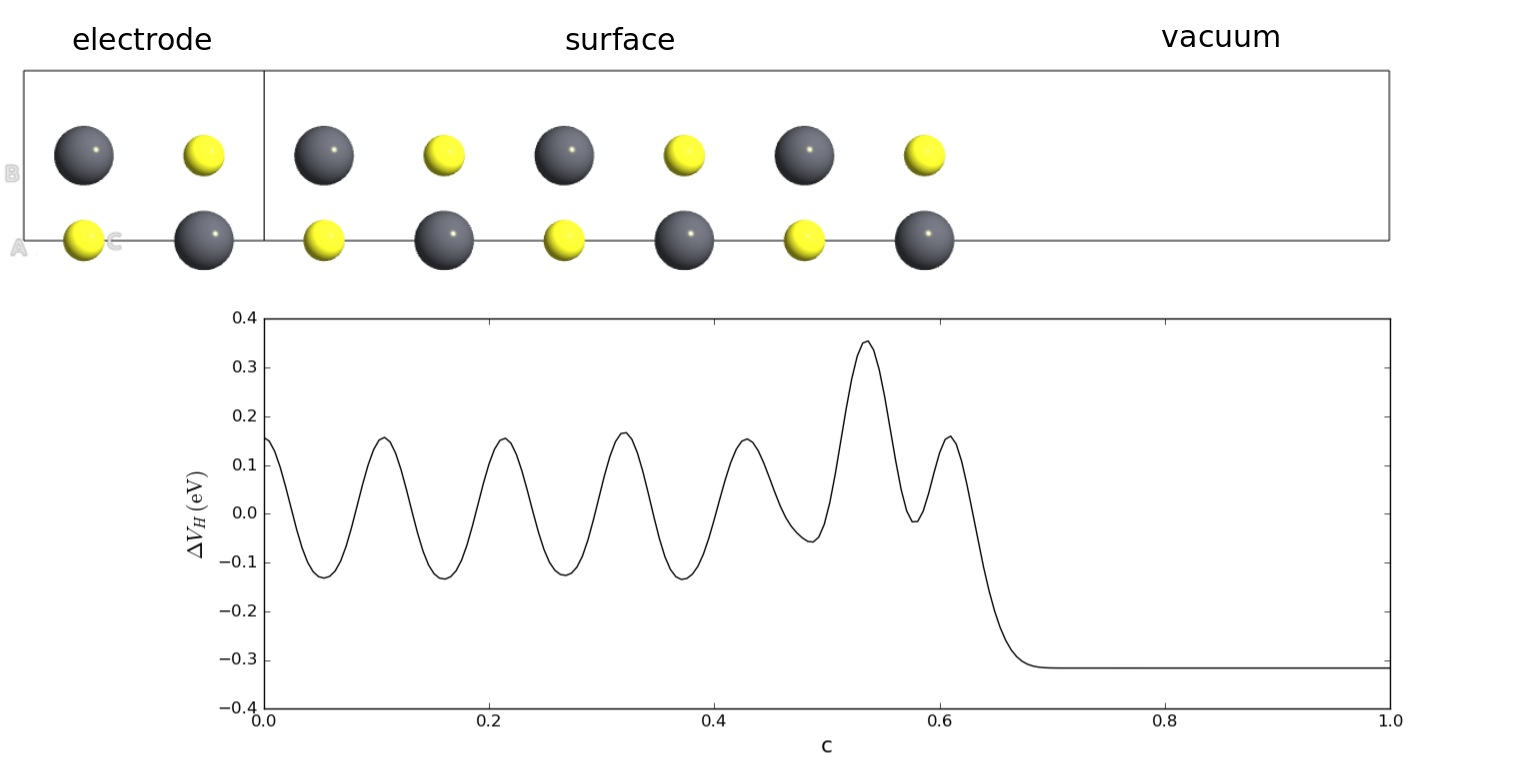
NEGF方法的优点
与传统的slab模型相比,基于格林函数方法的表面计算有明显的优势:
- slab模型是有限体系,只有有限的电子。因此,当表面上的分子与表面之间发生电荷转移时,表面模型的总电子数将发生变化,这将导致slab模型中的电子的化学势发生变化,这为计算的可靠性带来很大的问题。格林函数方法通过将表面耦合于一个无限大的电子池(化学势固定的电极)避免了这一问题。
- 性质计算随slab模型的厚度的收敛很麻烦,常常需要多种校正以避免晶胞重复之间的相互作用。而在QuantumATK格林函数计算中,由于边界条件的合理选择,表面性质随表面厚度的收敛非常容易,详见下文。
单电极的NEGF计算
如前所述,格林函数表面模型有一个电极和一个表面区域(或称中间区域)组成。在QuantumATK的语言里,可以称之为只有一个电极的器件结构。和其他QuantumATK器件(NEGF)计算一样,计算由两步完成:
- 首先进行电极块体材料电子态计算,这一步通常很快。
- 接下来计算表面区域的基态,过程中确保电极–表面的连接处电子态匹配。
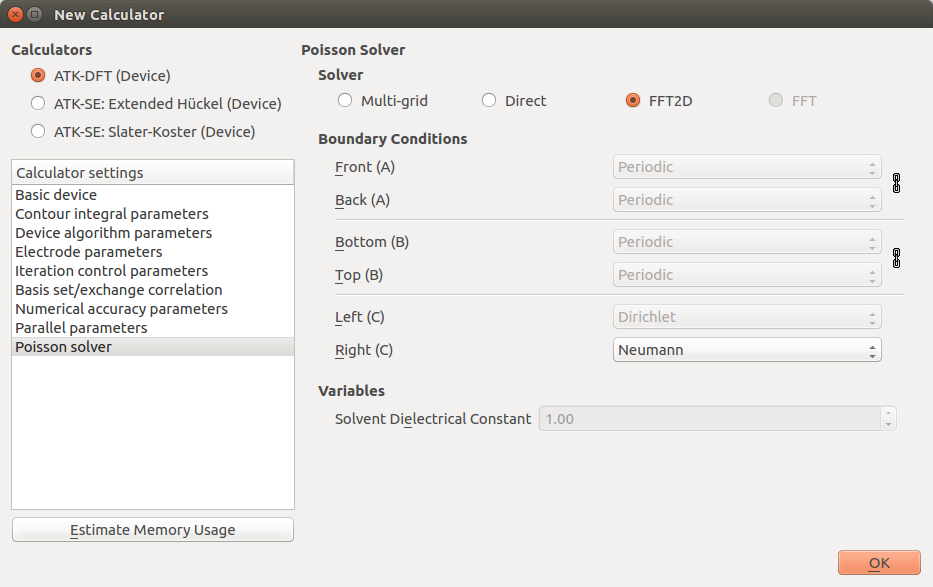
如下图所示,在晶胞C方向使用了三种不同的边界条件。电极部分向左方向采用周期边界条件,而在电极–表面处采用狄利克雷(Dirichlet)边界条件。而在表面一侧,Neumann边界条件是最自然合理的。

Ag(100) 表面的功函数
接下来,我们用 DFT 和格林函数方法计算 Ag(100)表面的功函数。基本操作步骤概括如下:
- 使用 Builder 建模工具从张力优化过的银块体构建表面结构,确定幽灵原子(Ghost atom);
- 使用 Scripter 创建计算基态的脚本,并保存差别静电势(Electrostatic difference potential;EDP)和化学势;
- 使用 1D Projector 工具查看 EDP 结果;
- 从 EDP 和化学势结果计算功函数。
构建表面模型
首先我们从银的块体结构出发,创建 (100) 表面。为此,首先使用LDA泛函、FHI赝势和SingleZetaPolarized基组对银的块体进行优化。
创建一个新的VNL project,下载包含优化过的结构的NetCDF文件:silver.nc 和 silver.py。将文件保存至项目文件夹下,注意到银的能带结构计算结果也计算好了,后面我们看到这是有用的。
你可以参考其他相关教程学习如何进行结构优化和能带计算。
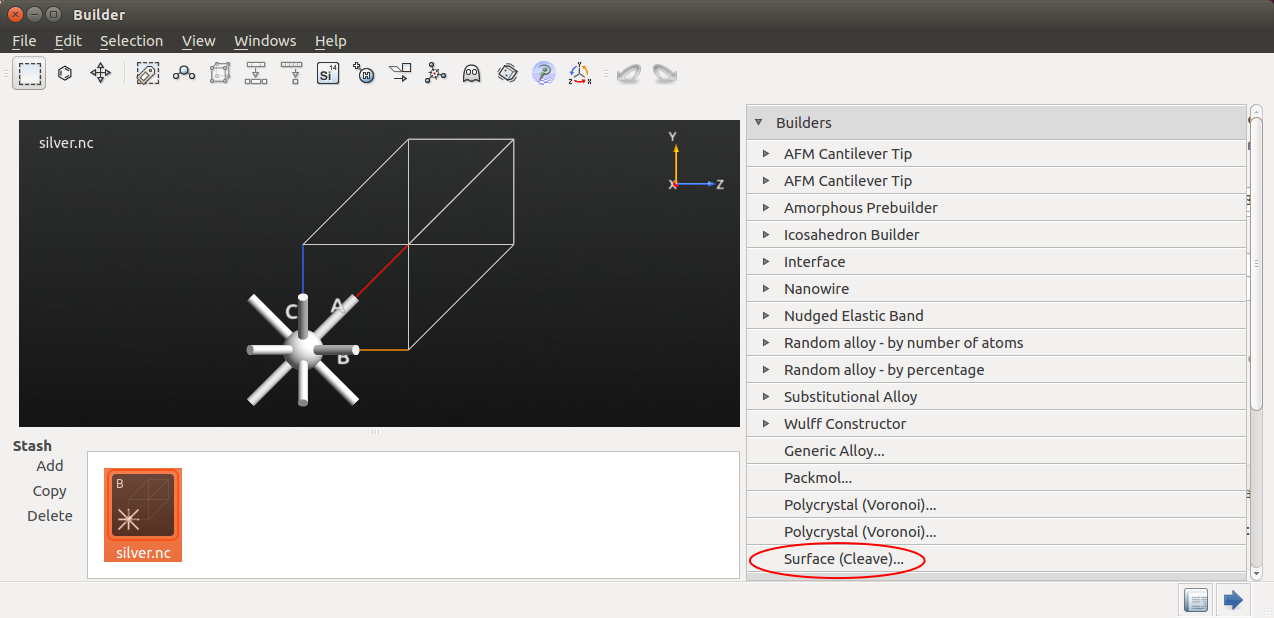
将弛豫过的块体结构拖动到 Builder,确认LDA-SZP结构优化得到的晶格常数为 4.148Å。之后选择右侧Builder→Surface (Cleave) tool。
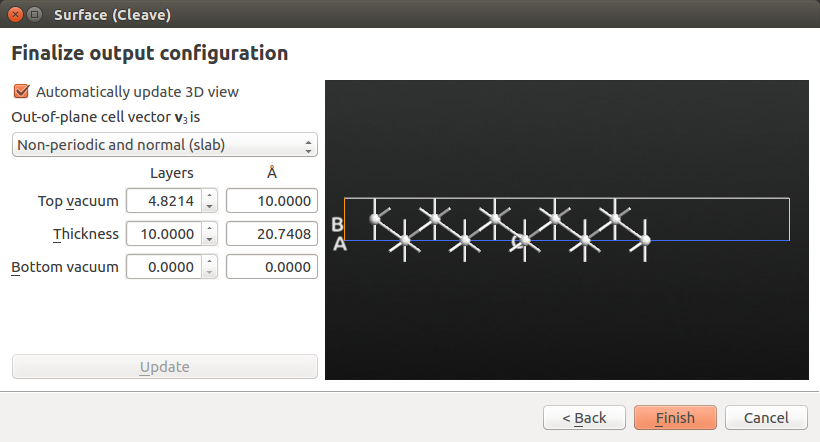
使用这个工具可以获得银晶体在100方向上的表面:点击Next两次,选择“Non-periodic and normal (slab)”,厚度为10层金属原子,如下图。
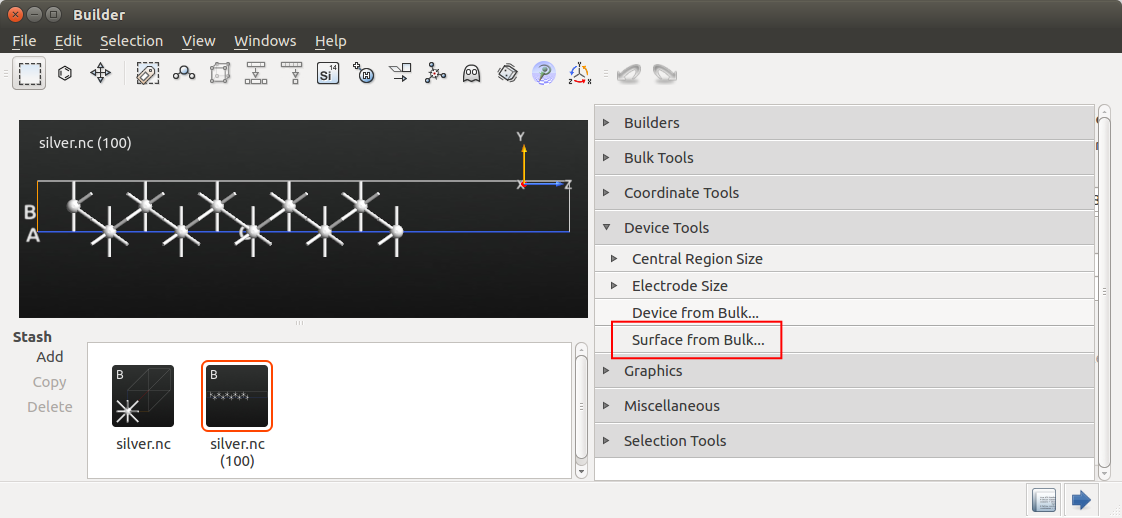
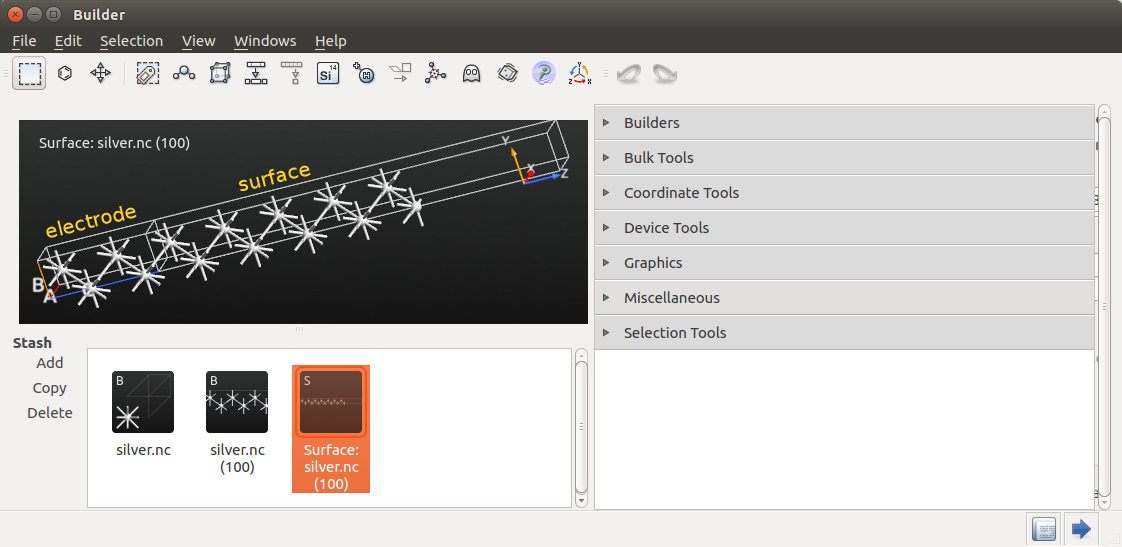
在下方stash里可以看到silver.nc(100)结构。双击选中它,点击右侧Device Tools → Surface From Bulk,创建用于格林函数计算的表面模型。
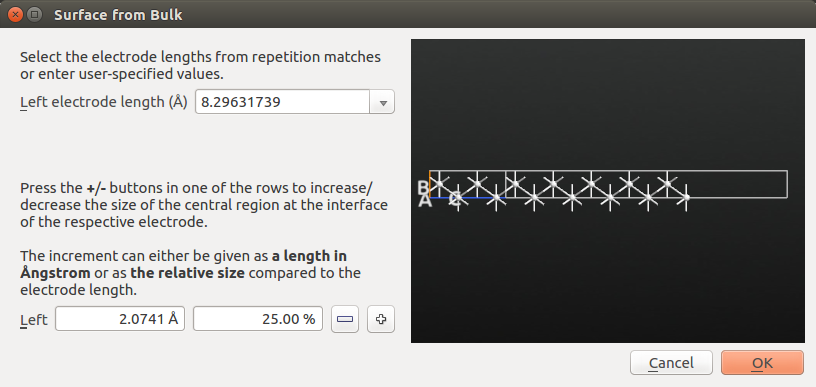
Surface from Bulk 工具可以选择电极和表面(这里标记为central region),默认的电极长度 8.3Å 应该正好。你还可以修改central region的长度。
点击 OK 将结构添加到Stash。结构名称前面自动添加了Surface。
幽灵原子(Ghost atom)
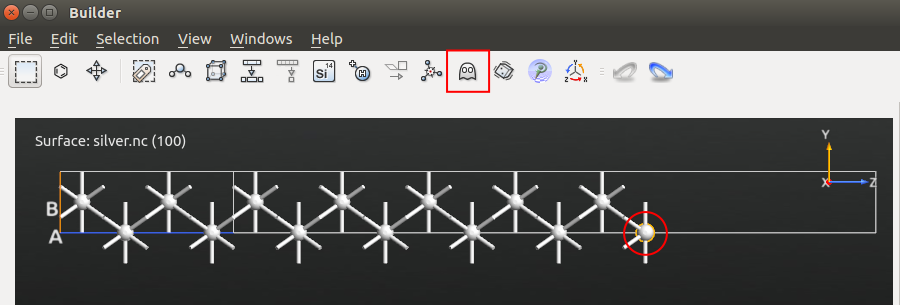
使用局域化的基组进行功函数计算,需要在紧邻表面上增加幽灵原子(Ghost atom)(详见:https://docs.quantumwise.com/tutorials/work_function_ag_100/work_function_ag_100.html#work-function-ag-100)。最方便的做法是将表面一层原子转换为幽灵原子。
这个原子现在变成了只有基组没有原子核的幽灵原子。
点击右下角箭头将此结构发送到 Script Grenerator去设置并进行格林函数计算。
进行计算
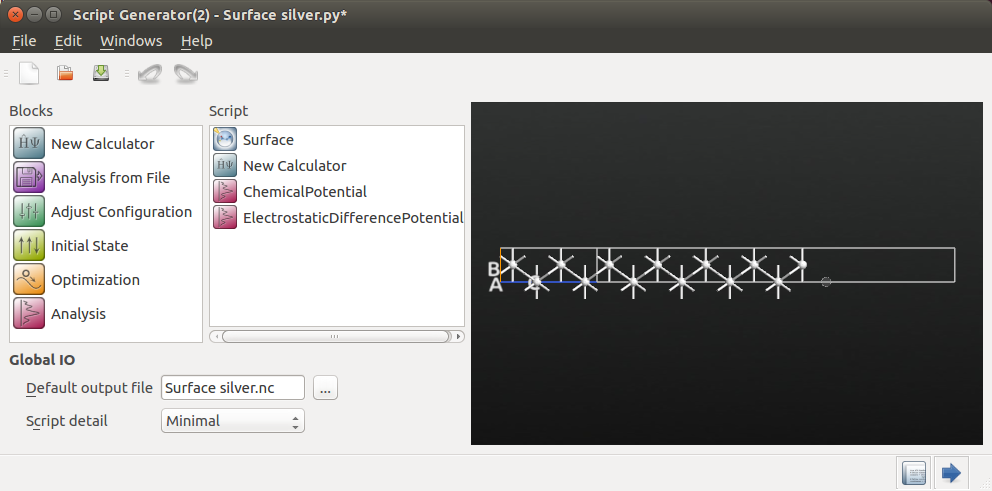
在 Script Generator 里双击添加如下计算步骤:
- New Calculator;
- Analysis→ChemicalPotential;
- Analysis→ElectrostaticDifferencePotential.
双击打开 New Calculator,在 Basic device 里,选择 LDA 交换关联泛函和 9x9x100 的 k 点。
QuantumATK器件计算时,C方向需要选择很大的k点(这里是100),详见教程使用QuantumATK研究电子输运。 C方向k点仅用于电极部分计算,而不用于主要区域计算,这是因为central region 定义为非周期性体系,因此C方向k点只需要1。
接下来,找到 Basis set/exchange corelation 设置,选择 SingleZetaPolarized基组。最后,在Poisson Solver设置里,将右侧C表面的的边界条件改为Neumann。
环路积分
NEGF方法使用复平面内的环路积分(Contour Integral)来计算格林函数。如果使用的赝势包含深能级(半芯)态时,Contour Integral默认参数Integral lower bound和Circle points可能需要增加。(详见教程 使用QuantumATK研究电子输运的有关章节)
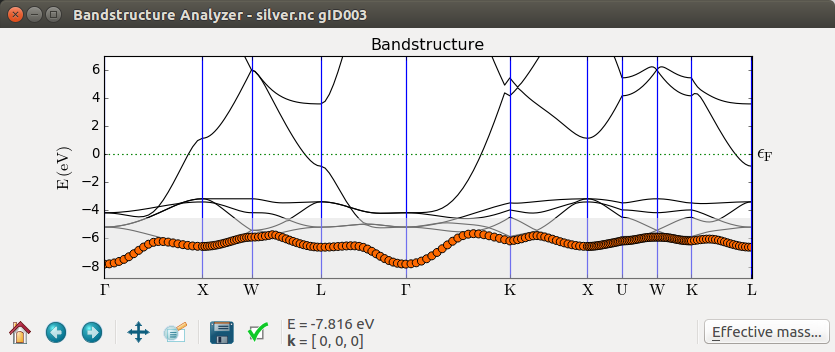
因此,最好先检查块体的能带,以确保最低的能带处于lower bound之上。这里,我们可以从文件silver.nc保存的能带进行判断,如下图。
最低能量本征值大约位于费米能级下7.8eV(0.29 Hartree),远高于环路积分的能量窗口边界(费米能级下1.5 Hartree),因此不需要改变默认设置。
保存脚本并运行
返回Script Generator 主窗口,将默认输出文件名改为silver_gfs.nc,将脚本保存为silver_gfs.py。如果需要也可以在这下载脚本:silver_gfs.zip。
将脚本发送至Job Manager或使用终端运行。在笔记本电脑上,此计算大于需要4分钟。
结果分析
计算结束后,NetCDF文件silver_gfs.nc出现在LabFloor里,里面包含了带有收敛计算的表面结构,化学势和差别静电势(EDP)。
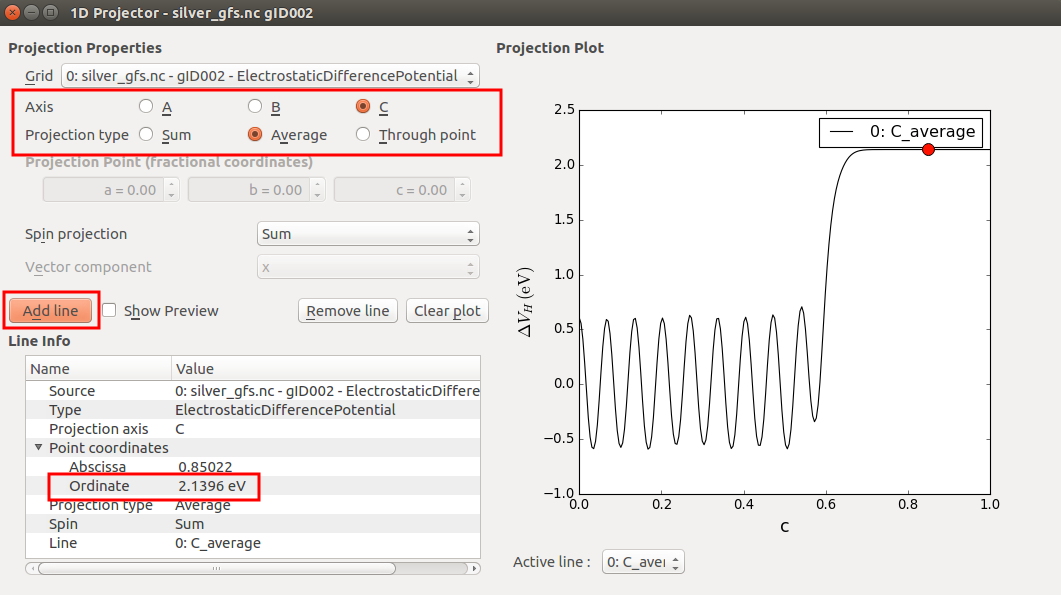
先查看表面方向的静电势分布情况。选中EDP,打开右侧1D Projector工具。
EDP是三维格点数据,但是1D Projector可以将其延任意方向投影,将EDP在C方向投影如下。
Ag(100)表面的功函数可以通过计算真空区域的(常数)EDP与化学势(在格林函数表面计算中是电极的化学势)的差别得到: $$ \mathrm{WF} = \delta V_\mathrm{H}^\mathrm{c=1} - \mu $$
将红色圆点移动到最右侧(c=1)可以得到$\delta V_\mathrm{H}^\mathrm{c=1}$=+2.14 eV。
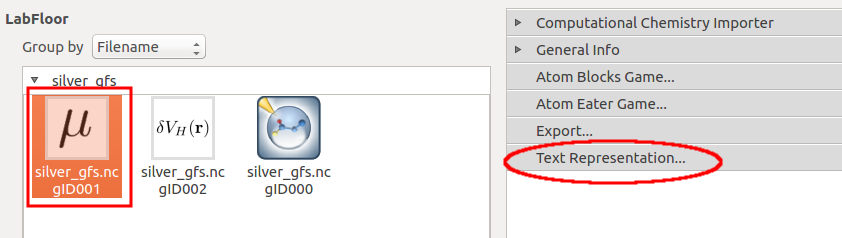
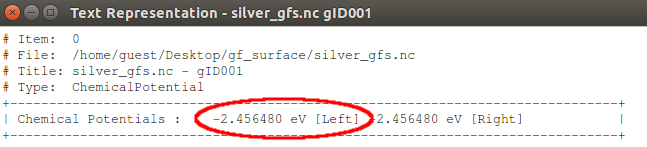
选中化学势图标,使用 Text Representation 可以读取数值为 $\mu$= -2.46 eV。
理论计算得到的功函数为4.6eV,与实验得到的4.64eV非常接近。注意到表面结构并没有弛豫,也就没有考虑表面重构等的影响。实际计算时可以添加OptimzeGemoetry进行结构弛豫。
功函数对金属层数的收敛性
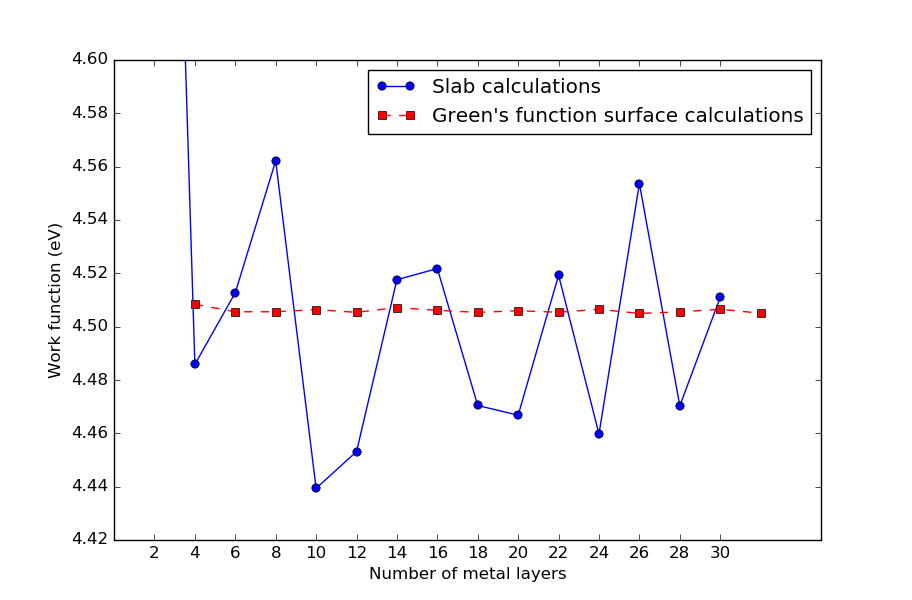
最后,我们看一下格林函数方法与传统slab方法的区别。下图显示了Ag(100)表面功函数预测结果与银原子层数的关系。格林函数使用的方法与上面类似,不过使用了两层幽灵原子。
结果清楚的表明,与传统的slab模型相比,使用格林函数表面模型进行计算得到的功函数对原子层数的收敛性要快得多。
如果想重复上述结果,可以下载这两个脚本进行计算:wf_slab.zip和wf_surface.zip,并使用这个脚本plot1.zip进行作图。