目录
拓扑绝缘体
拓扑绝缘体是具有如正常绝缘体一样的块体能隙,但是在表面具有导电态的电子材料。这些态受材料的非平庸拓扑指数的拓扑保护,并且不会被任何扰动所移除。这些表面态的二维能量动量关系具有一个类似于石墨烯的“狄拉克锥”结构。拓扑绝缘体由此构成由奇异物理现象支配的新一类量子物质,并可能在将来运用于电子器件中。文献[HK10]和[QZ11]提供了这个高度活跃的研究领域的近期综述。
在本实例中您将学到如何使用ATK-DFT来研究<chem>Bi2Se3</chem>化合物,它是一个三维强拓扑绝缘体。最近有报道一个<chem>Bi2Se3</chem>薄膜导线连接双端器件设置的非平衡格林函数DFT计算[CMS+15]。然而,本实例专注于块体计算和表面态的性质。特别地,你将:
- 使用VNL晶体Builder来创建<chem>Bi2Se3</chem>晶体结构。
- 研究包含和不包含SOC的<chem>Bi2Se3</chem>块体能带结构。
- 构建一个<chem>Bi2Se3</chem>平板构型并计算SOC能带结构,展现出上面提到的表面态。
- 计算费米能附近的态密度,很好地阐释了块体带隙中的狄拉克锥。
- 研究表面态在材料中的渗透深度。
- 绘出表面态的自旋分辨费米面,并研究面内自旋方向如何在费米面上变化。
- 计算<chem>Bi2Se3</chem>的拓扑不变量。
注意!
考虑自旋轨道耦合(SOC)对于正确描述拓扑绝缘体的电子结构是至关重要的。
构建Bi2Se3晶体
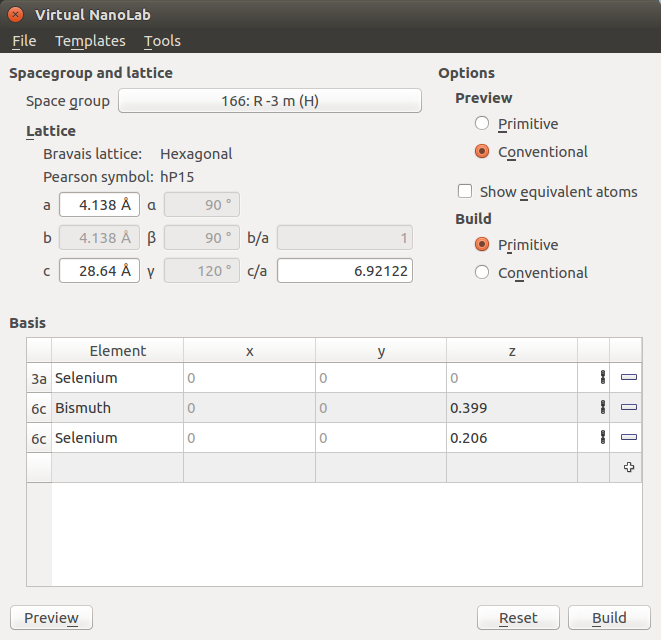
打开VNL中Builder![]() 并点击Add‣From Plugin‣Crystal Builder。正如文献[ZYZ+10]所述,<chem>Bi2Se3</chem>晶体是斜方六面体的并且属于$\mathrm{R \overline{3} m}$空间群。它具有晶格常数a=4.138 Å和 c=28.64 Å,Bi位的内坐标$\mu$=0.399,Se位的内坐标$\nu$=0.206。<chem>Bi2Se3</chem>的基本单胞称为一个五重层(QL),包含5个原子:一个Se原子在坐标(0, 0, 0) ,内坐标为($\pm\mu$,$\pm\mu$,$\pm\mu$)的Bi原子,和内坐标为($\pm\nu$,$\pm\nu$,$\pm\nu$)的Se原子。
并点击Add‣From Plugin‣Crystal Builder。正如文献[ZYZ+10]所述,<chem>Bi2Se3</chem>晶体是斜方六面体的并且属于$\mathrm{R \overline{3} m}$空间群。它具有晶格常数a=4.138 Å和 c=28.64 Å,Bi位的内坐标$\mu$=0.399,Se位的内坐标$\nu$=0.206。<chem>Bi2Se3</chem>的基本单胞称为一个五重层(QL),包含5个原子:一个Se原子在坐标(0, 0, 0) ,内坐标为($\pm\mu$,$\pm\mu$,$\pm\mu$)的Bi原子,和内坐标为($\pm\nu$,$\pm\nu$,$\pm\nu$)的Se原子。
晶格
基
然后明确原子的基来布置晶格,也就是输入Bi2Se3晶体的特定占位的内坐标和元素应该的占位:
- 点击 键并选择3a: (0,0,0)位,将元素从氢变为硒。
- 使用同样的过程两次来确定剩下的占位,但选择6c: (0,0,z) 作为占位类型,并输入铋的内坐标z=0.399,硒的内坐标z=0.206。
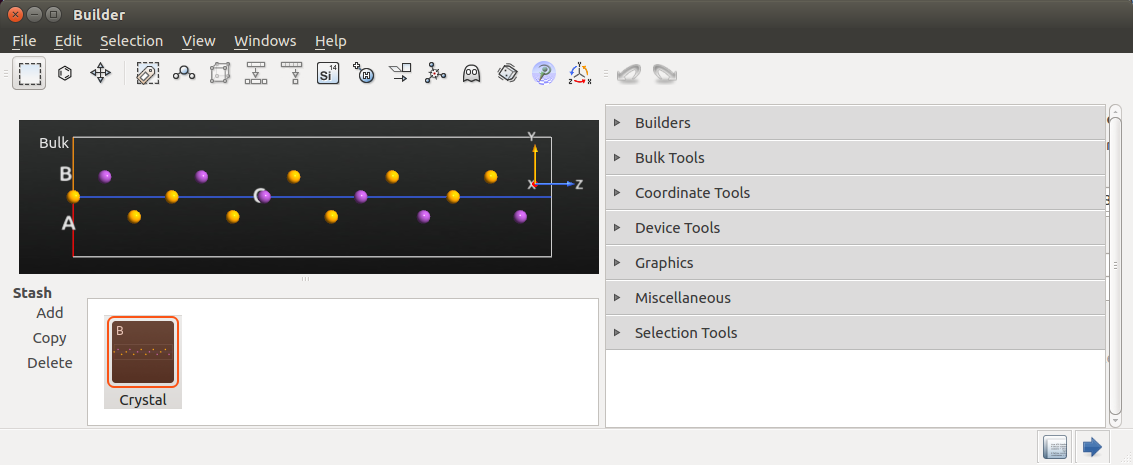
Crystal Builder窗口现在应该看起来如下图。点击Build来创建块体构型,它将出现在Builder Stash里。
您现在已经构建了总计有3个QLs和15个原子的<chem>Bi2Se3</chem>块体构型。继续下一个部分来开始对这个材料进行一些DFT计算。如果需要,你也可以在此下载块体构型:Bi2Se3_bulk_configuration.py
Bi2Se3块体能带结构
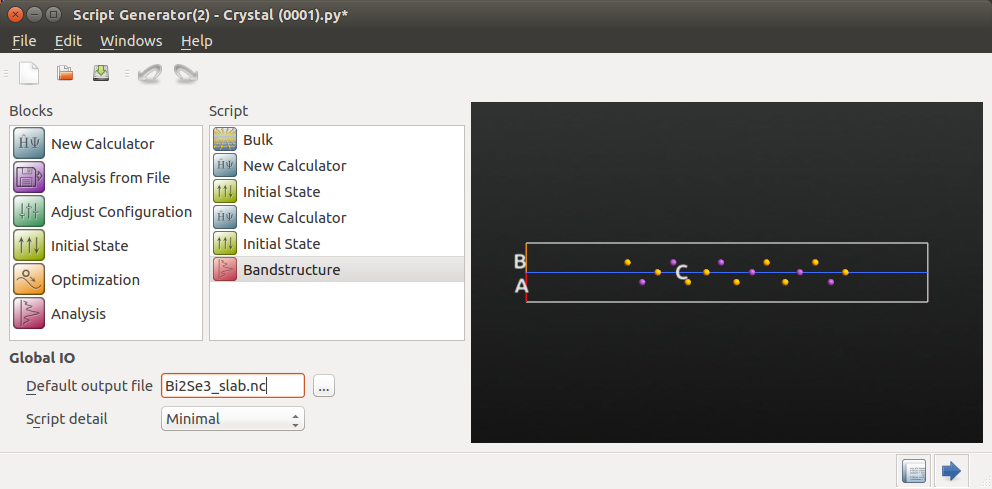
将块体构型送到Script Generator,并设置一个使用ATK-DFT的Python脚本来计算包含和不包含自旋轨道耦合的能带计算。脚本首先应计算自洽GGA态并执行能带分析,随后使用这个态作为自洽SOGGA态的初始猜测,同样后接能带分析。
Script Generator现在包含块体构型。添加 ![]() New Calculator,
New Calculator,![]() Analysis ‣ Bandstructure,和
Analysis ‣ Bandstructure,和 ![]() Initial State模块,如下所示。改变默认输出文件为
Initial State模块,如下所示。改变默认输出文件为 Bi2Se3_bulk.nc。
GGA计算
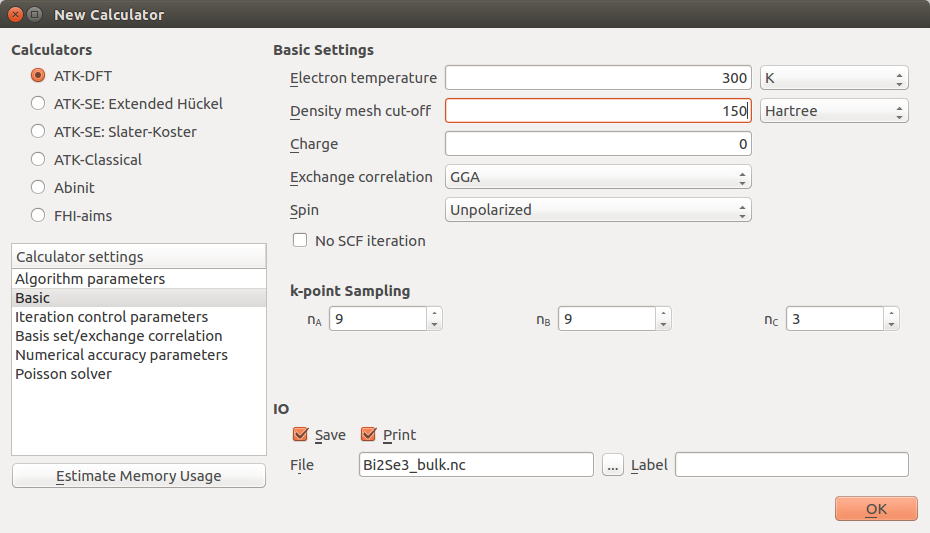
- 确保选择ATK-DFT计算器。
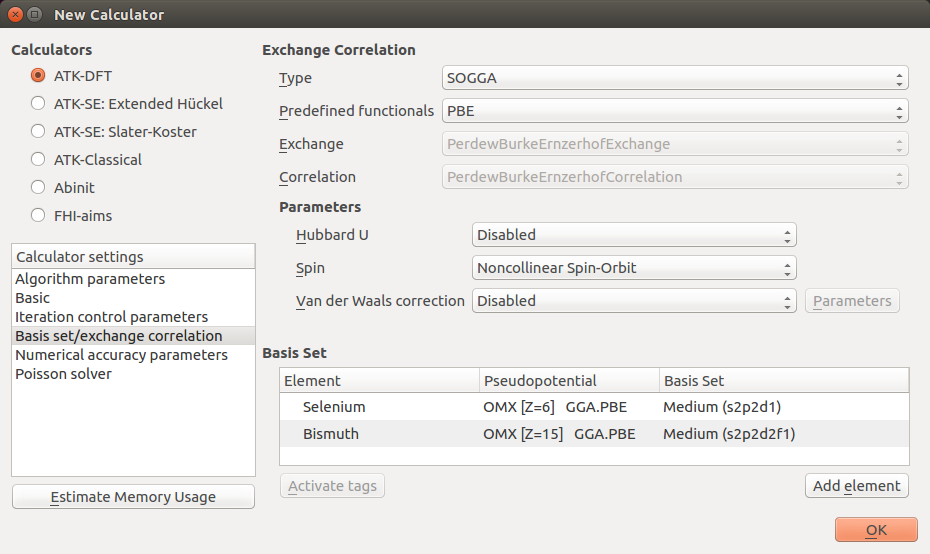
- 在Basis set/exchange correlation设置中,选择GGA并设置Se和Bi的赝势均为OMX类的Medium基组。
- 在Basic设置栏,将density mesh cut-off增加到150 Hartree,并设置一个9x9x3的k点网格。点击OK来保存设置。
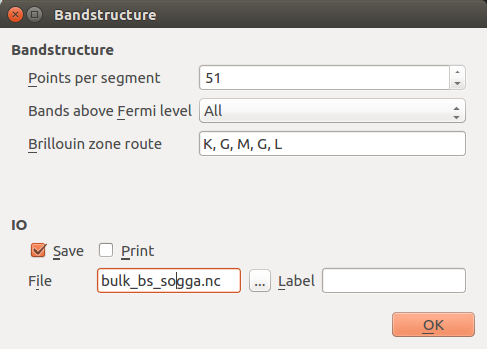
- 增加points per segment 为51以得到一个分辨良好的能带结构。
- 改变Brillouin zone route 为K, G, M, G, L。
- 改变IO文件为
bulk_bs_gga.nc。
SOGGA计算
打开第二个![]() New Calculator模块,并编辑设置参数同第一个计算器一样,但设置Spin参数为Noncollinear Spin-Orbit来做SOGGA计算。记得同样要设置赝势,能量截断和k点。
New Calculator模块,并编辑设置参数同第一个计算器一样,但设置Spin参数为Noncollinear Spin-Orbit来做SOGGA计算。记得同样要设置赝势,能量截断和k点。
接下来,打开第二个![]() Initial Stat模块,选择Initial state type为User spin,选中Use old calculation选项,并输入文件名为
Initial Stat模块,选择Initial state type为User spin,选中Use old calculation选项,并输入文件名为 Bi2Se3_bulk.nc(从这个文件读取GGA态)。
结果
Python脚本现已完成。将其保存为Bi2Se3_bulk.py。如果需要,你也可以在此处下载:Bi2Se3_bulk.py
使用Job Manager![]() 或者一个终端来执行它。这个任务将会花费一段时间,但是如果使用在2CPUs上的2MPI进程上并行执行,经过时间可缩短在40分钟左右。注意这需要总计大约15GB的可用内存!
或者一个终端来执行它。这个任务将会花费一段时间,但是如果使用在2CPUs上的2MPI进程上并行执行,经过时间可缩短在40分钟左右。注意这需要总计大约15GB的可用内存!
提示!
实例Basic troubleshooting guide for getting better performance提供了QuantumATK执行的注意事项,包括如何处理内存问题。
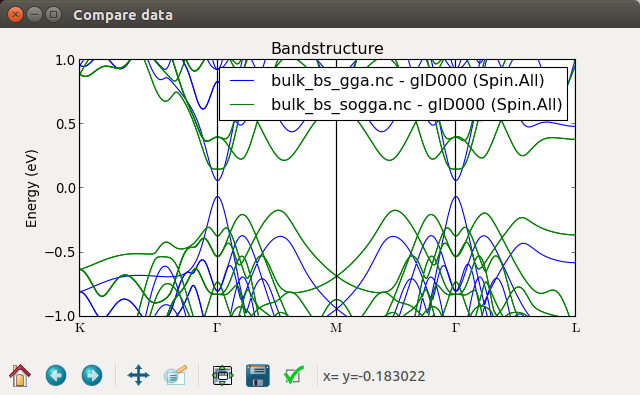
当计算完成时,VNL的LabFLOOR中包括三组数据:Bi2Se3_bulk, bulk_bs_gga, 和bulk_bs_sogga。后两个包含GGA和SOGGA的能带结构。高亮这两个能带项,并使用Compare Data插件来将它们绘出。
绘图如下所示。在计算中考虑自旋轨道耦合(SOGGA)对能带结构有一个显著的影响,并使在$\Gamma$点的直接带隙变大。然而,我们并没有见到任何能带穿过费米能级(最小的SOGGA能隙为0.3eV),所以<chem>Bi2Se3</chem>块体材料是绝缘体。
Bi2Se3表面:自旋轨道能带结构
您现在将创建一个<chem>Bi2Se3</chem>平板构型,并计算SOGGA能带结构,它将显示受拓扑保护的表面态在$\Gamma$点附近穿过带隙。
构造表面
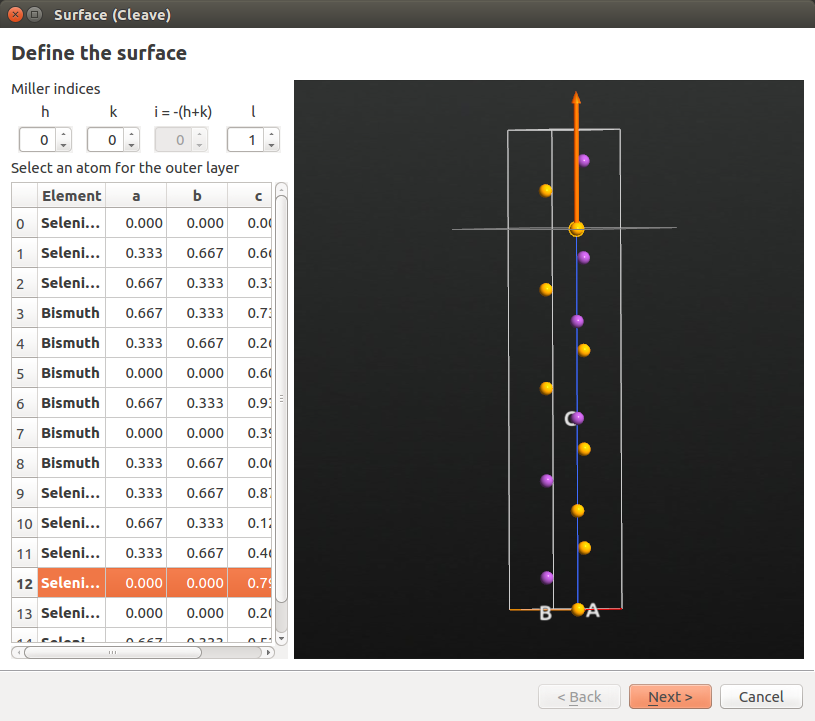
回到Builder,高亮<chem>Bi2Se3</chem>块体构型(名为Crystal),打开Builders ‣ Surface (Cleave)插件。选择Miller indices为(0001),并选择序号为12的硒原子作为平板中最顶原子。然后点击Next。
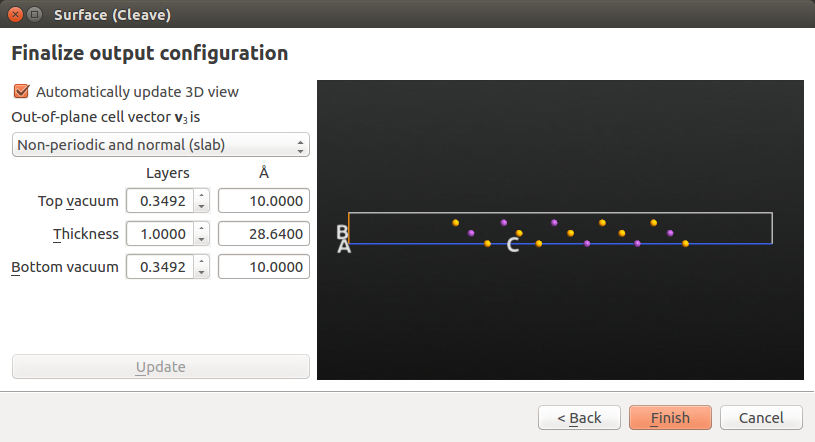
保留“Define surface lattice” 选择窗口的设置为默认值。在“Finalize output configuration” 选项中,选择一个Non-periodic and normal (slab)的out-of-plane cell vector,并设置上下真空层为10 Å。然后点击Finish。
平板构型,命名为Crystal (0001),现在就出现在Stash中。作为最后一步,高亮这一项并用Bulk Tools ‣ Lattice Parameters插件来将晶格类型转换为Hexagonal同时保持分数坐标不变:
DFT-SOGGA计算
您现在可以将平板构型送至Script Generator,并像上面块体的设置类似来设置SOGGA能带结构计算,但有略微不同:
- 您将不需要GGA能带结构分析。
- 使用
Bi2Se3_slab.nc作为默认输出文件。 - 使用一个9x9x1的k点网格(平板沿C方向不是周期的)。
- 降低电子温度从300k到50k。这将改善接近费米能级的电子占据的DFT描述。
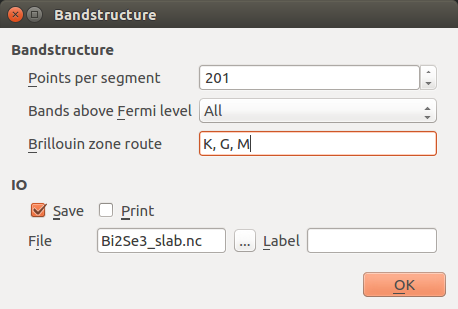
- 对于SOGGA能带结构分析使用points per segment为201, Brillouin zone route为K–G–M。
或者,您可以简单地跳过上述直接到下一个部分使用一个预制的具有一些附加特征的Python脚本。
便捷的Python脚本
点击这里:Bi2Se3_slab.py来下载一个使用上面列出的步骤制作的Python脚本,但也有少许额外特征:
- “MemoryUsage”功能用来在计算执行前即刻估计GGA和SOGGA计算所需的内存 。
- SOGGA计算器被构造为GGA计算器的一个副本,并随后相应的被修改。
- 对于非共线计算使用了一个特殊的密度混合算法。
使用Job Manager![]() 或者在一个终端运行计算。如果在2 CPUs上的2并行MPI执行,这个任务将会花费大致30分钟。
或者在一个终端运行计算。如果在2 CPUs上的2并行MPI执行,这个任务将会花费大致30分钟。
提示
如果您在计算过程中查看日志文件,您将会看到对于GGA计算每MPI进程估计的所需内存峰值为756MB,而对于SOGGA是每MPI进程3.8GB。这些是估计,在实际过程中您应该预期总计算需要大约5GB每MPI进程。
GGA: +----------------------------------------------------------+ | Memory usage estimate | | -------------------------------------------------------- | | Base: Sparse matrices 44 Mbyte | | Base: GridTool+Basis set 100 Mbyte | | Base: SCF history 442 Mbyte | | Base: NLEngine 70 Mbyte | | Base: Grid terms 39 Mbyte | | Sum of the base terms 696 Mbyte | | -------------------------------------------------------- | | Peak: Diagonalization 60 Mbyte | | Peak: Grid terms 19 Mbyte | | -------------------------------------------------------- | | Estimated Peak memory requirement 756 Mbyte | +----------------------------------------------------------+ SOGGA: +----------------------------------------------------------+ | Memory usage estimate | | -------------------------------------------------------- | | Base: Sparse matrices 272 Mbyte | | Base: GridTool+Basis set 100 Mbyte | | Base: SCF history 2726 Mbyte | | Base: NLEngine 70 Mbyte | | Base: Grid terms 157 Mbyte | | Sum of the base terms 3326 Mbyte | | -------------------------------------------------------- | | Peak: Diagonalization 446 Mbyte | | Peak: Grid terms 58 Mbyte | | -------------------------------------------------------- | | Estimated Peak memory requirement 3772 Mbyte | +----------------------------------------------------------+
结果
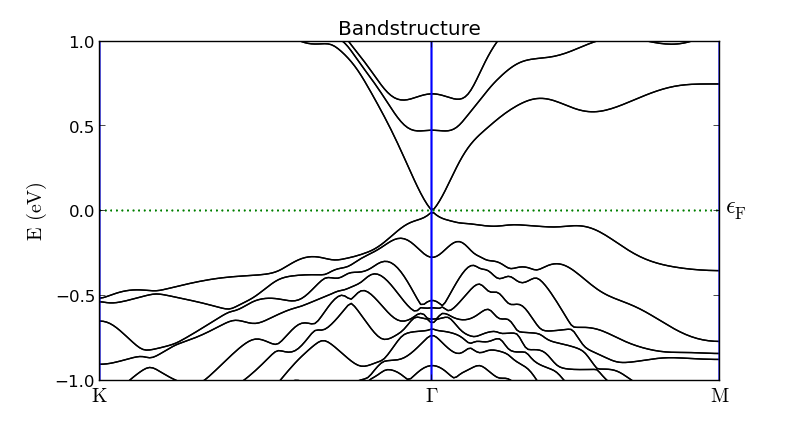
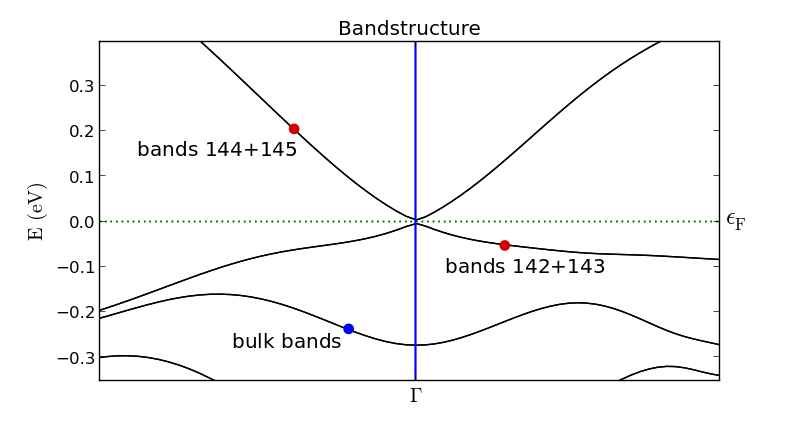
VNL LabFloor现在应包含计算的结果。选择能带结构项,使用Bandstructure Analyzer来绘出。
计算得出的<chem>Bi2Se3</chem>平板的能带结构显示如下。能带展现在$\Gamma$点费米能级附近-这些是表面态。有四个这样的表面态穿过费米能级(红点示出);能带142和143在费米能紧下面形成一个单简并能带,而能带144和145在费米能之上形成一个简并能带(蓝点示出)。很清楚狄拉克锥位于块体带隙之中。在表面能带的价带和导带之间有一个很小的带隙,大小为7meV。这是使用平板模型所导致的有限尺寸效应,源于平板相对侧的表面能带的相互作用。对于一个大的平板,带隙将会减少。
DOS分析:狄拉克锥指纹
正如在介绍中所述,接近费米能级的表面态电子结构类似于一个狄拉克锥,也就是电子动量线性依赖于能量。由于表面态是在块体能隙中唯一呈现的态,我们应期许接近费米能的电子态密度为线性的。作为一个后SCF分析,很容易计算和绘出DOS:
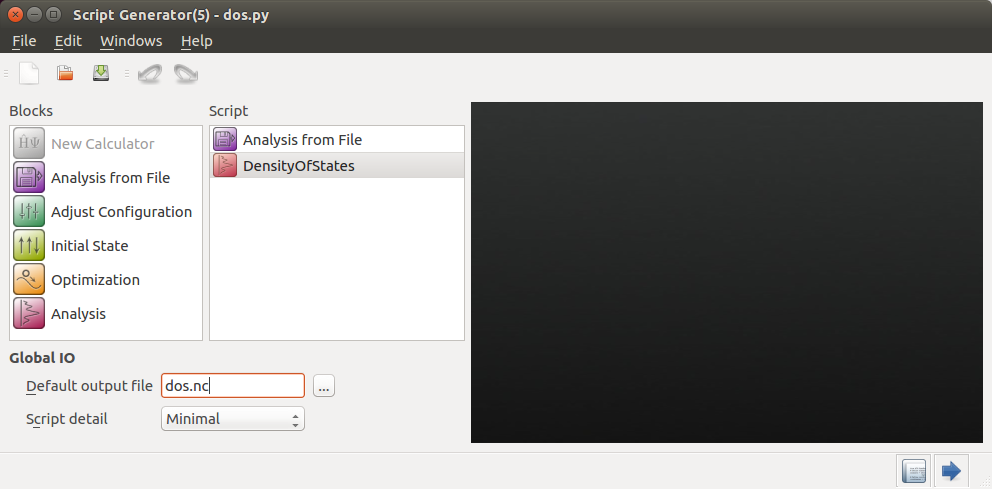
打开Script Generator后添加 ![]() Analysis from File和
Analysis from File和 ![]() Analysis ‣ DensityOfStates模块。改变默认输出文件为
Analysis ‣ DensityOfStates模块。改变默认输出文件为 dos.nc。
打开第一个模块,指向Bi2Se3_slab.nc 文件和Object id glD001,这是自洽的SOGGA态。
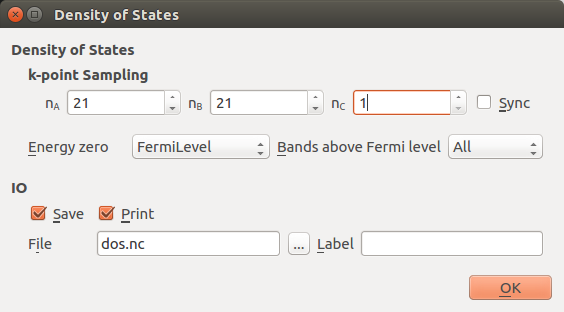
然后打开DensityOfStates analysis模块,设置沿着kx和ky的一个稠密的k点取样,21x21x1。您将需要点掉sync选项。切记:在本例中对$\Gamma$点取样很重要,所以我们使用一个奇数k网格。
保存脚本为 dos.py 并运行。您也可以在这里下载它:dos.py。
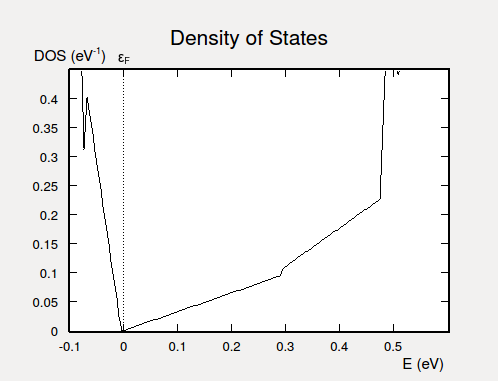
然后在LabFloor中找到DOS项,并使用2D Plot插件来对其可视化。如下图所示,对其进行一些放大您应会看到预期的DOS线性依赖于能量。DOS在E=0.47 eV的陡增应归于最低的块体价带。
表面态的穿透深度
对于接近狄拉克点的受拓扑保护的表面态的一个基本特征是,它们高度局域在表面区域。穿透于块体材料的深度可能只有2-3nm这么小[ZYZ+10]。而且,在一个能带结构计算中观察到的简并表面态在每个特定的k点都由自旋相反的态组成并位于平板的相对侧。
现在您将通过为能带144和145在狄拉克锥上一个指定k点进行BlochState analysis来研究这个现象。您将随后将两个Bloch态投影到<chem>Bi2Se3</chem>平板单胞的C轴上,并绘出非共线自旋矢量的大小和方向作为C坐标的一个函数。
计算
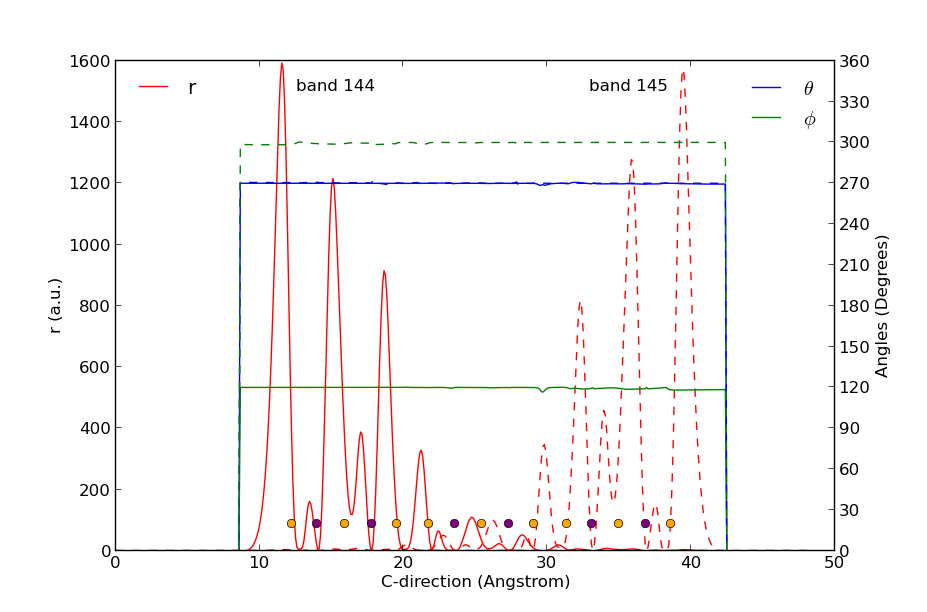
您将需要以下两个脚本:bloch_states.py和spinVector.py。下载这两个脚本并使用Job Manager或者在一个终端执行第一个(bloch_states.py)。它从Bi2Se3_slab.nc读取SOGGA态,为k点[0, 0.04, 0]执行两个BlochState分析,并为两个Bloch态计算长度r和极角$\theta$和$\phi$并绘出。
结果图形如上所示。底部的黄色和紫色点分别指出了Se和Bi原子的位置。这两个态清楚地位于平板的两侧(红线)并且在平板中间有非常小的重叠。两个态的极角$\phi$都是270°(蓝线),但是能带144的面内角是120°而能带145的面内角被扭转了180°变为300°(绿线)。这两个自旋态由此指向相反方向!
费米面和自旋方向
最后,研究在狄拉克锥邻近的<chem>Bi2Se3</chem>平板的费米面很有意思。通过在以$\Gamma$点为中心的一个稠密k网格上取样能带结构,这将很容易完成。
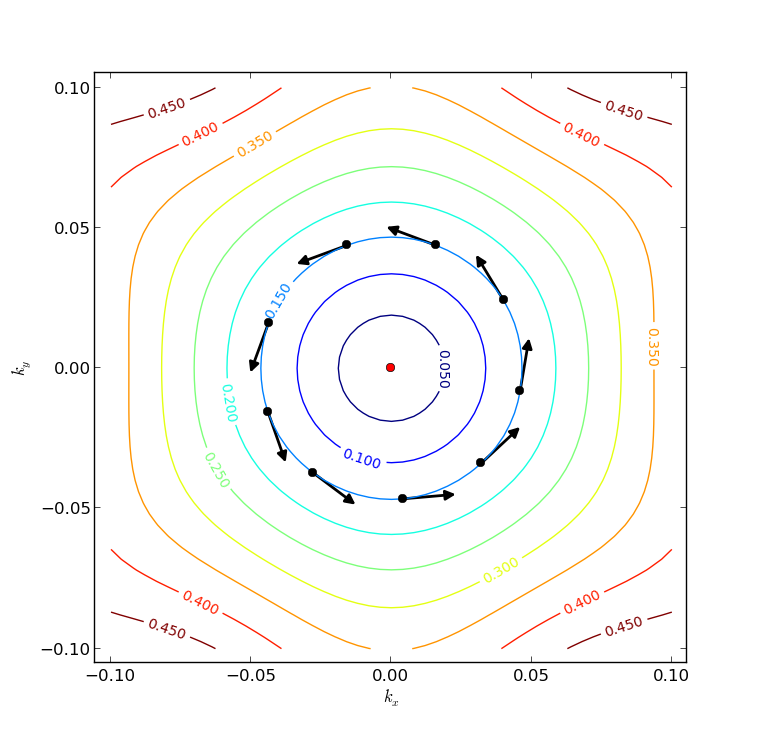
下载并执行这个预制的脚本:fermi_surface.py。它从Bi2Se3_slab.nc读取SOGGA态,在一个$kx\times ky=51\times51$的网格上对所有点进行能带结构分析,并对能带144中的表面态创建一个本征能量等高线图。
结果图如上所示。正如对一个狄拉克锥的预期,接近顶点(红点)的费米面是环形的,但对本例来说随着能量变高,形状变得更像六角形。 Python脚本也提取出对应于EF=0.15 eV的等高线并对围绕这个等高线每隔10个($kx$, $ky$)点计算一个Bloch态。对每一个点,一个箭头表明了面内自旋方向($\phi$)。很明显,自旋随着环绕狄拉克点旋转了2$\pi$。
对此的解释很简单:时间反演对称需要在动量k和-k的态具有相反的自旋。然而,对于源于一个单表面的表面态的狄拉克锥不是自旋简并的。随着绕费米面行进,自旋由此必须随着k而转动。更多细节参见[HK10]。
拓扑不变量
一个三维拓扑绝缘体的性质是由四个拓扑不变量来决定的[FKM07],[MB07],[Roy09],它们描述了在特定k点上的能带结构的性质,也就是$\Gamma$点和布里渊区边界。 第一个拓扑不变量描述了在不同特殊k点波函数对称性的不同。这个不变量辨别“强”拓扑绝缘体,当它呈现时,系统将会有拓扑保护的表面能带。这个拓扑不变量对于原子无序是鲁棒的并且任何非时变扰动不会移除表面能带。 对于一个具有反演对称的体系,拓扑不变量可以通过Bloch函数在8个特殊布里渊区点的对称性来计算[FK07], $\Gamma_{i=(n_1,n_2,n_3)} = \frac{1}{2}(n_1 {\bf b_1} + n_2 {\bf b_2} + n_3 {\bf b_3})$, 其中$\bf b_i$是倒格矢,$n_i=0,1$。 令$\psi_{i, n}$为在$\Gamma_{i}$的第n个占据布洛赫函数,我们定义对称函数 $\delta_i = \Pi_n \sqrt{\langle \psi_{i, n}| \Theta | \psi_{i, n} \rangle}$ 其中$\Theta$是反演算子。当我们知道了对称函数,强拓扑不变量$\nu_0$ 就可以由此给出 $(-1)^{\nu_0}=\Pi_{i=1}^{8} \delta_i .$ 另有三个弱不变量,$\nu_1,\nu_2和\nu_3$,由四个$\delta_i$乘积得到,$\Gamma_{i}$属于同一个平面: 弱不变量对原子无序不是鲁棒的,且不能保证金属表面带的存在。
计算拓扑不变量的Python脚本
下载脚本TopologicalInvariant3D.py,在其中实现为计算拓扑不变量而给出的上述方程。这个脚本将只对具有反演对称性的系统凑效。用法的一个例子以下面的python脚本给出。
from TopologicalInvariant3D import topologicalInvariant3D bulk_configuration = nlread("bi2se3_bulk_sogga.nc", BulkConfiguration)[0] print '-----------------------------------' print 'Topological Invariants = ', topologicalInvariant3D(bulk_configuration) print '-----------------------------------'
当运行后会产生如下输出
----------------------------------- Topological Invariants = [1 0 0 0] -----------------------------------
我们看到<chem>Bi2Se3</chem>是一个强三维拓扑绝缘体,因为$\nu_0=1$,而三个弱不变量都为0。 您现在可以容易地筛选出一些具有反演对称性的三维材料的拓扑指数来算出它们是否是强或者弱拓扑绝缘体。
参考文献
[CMS+15] Po-Hao Chang, Troels Markussen, Søren Smidstrup, Kurt Stokbro, and Branislav K. Nikolić. Nonequilibrium spin texture within a thin layer below the surface of current- carrying topological insulator bi2se3: A first-principles quantum transport study. Phys. Rev. B, 92:201406, 2015. doi:10.1103/PhysRevB.92.201406.
[FK07] Liang Fu and Charles L Kane. Topological insulators with inversion symmetry. Physical Review B, 76(4):045302, 2007. doi:10.1103/PhysRevB.76.045302.
[FKM07] Liang Fu, Charles L Kane, and Eugene J Mele. Topological insulators in three dimensions. Physical Review Letters, 98(10):106803, 2007. doi:10.1103/PhysRevLett.98.106803.
[HK10] (1, 2) M. Z. Hasan and C. L. Kane. Colloquium: Topological insulators. Rev. Mod. Phys., 82:3045–3067, Nov 2010. doi:10.1103/RevModPhys.82.3045.
[MB07] Joel E Moore and Leon Balents. Topological invariants of time-reversal-invariant band structures. Physical Review B, 75(12):121306, 2007. doi:10.1103/PhysRevB.75.121306.
[QZ11] Xiao-Liang Qi and Shou-Cheng Zhang. Topological insulators and superconductors. Rev. Mod. Phys., 83:1057–1110, Oct 2011. doi:10.1103/RevModPhys.83.1057.
[Roy09] Rahul Roy. Topological phases and the quantum spin hall effect in three dimensions. Physical Review B, 79(19):195322, 2009. doi:10.1103/PhysRevB.79.195322.
[ZYZ+10] (1, 2) Wei Zhang, Rui Yu, Hai-Jun Zhang, Xi Dai, and Zhong Fang. First-principles studies of the three-dimensional strong topological insulators Bi2Te3, Bi2Se3 and Sb2Te3. New Journal of Physics, 12(6):065013, 2010. doi:10.1088/1367-2630/12/6/065013.
本文翻译:王吉章