这是本文档旧的修订版!
非线性光学入门案例:LiH的静态α、β、γ值计算
背景
文献
Zhongwei Hu, Jochen Autschbach, and Lasse Jensen, Simulating Third-Order Nonlinear Optical Properties Using Damped Cubic Response Theory within Time-Dependent Density Functional Theory, J. Chem. Theory Comput. 2016, 12, 1294−1304
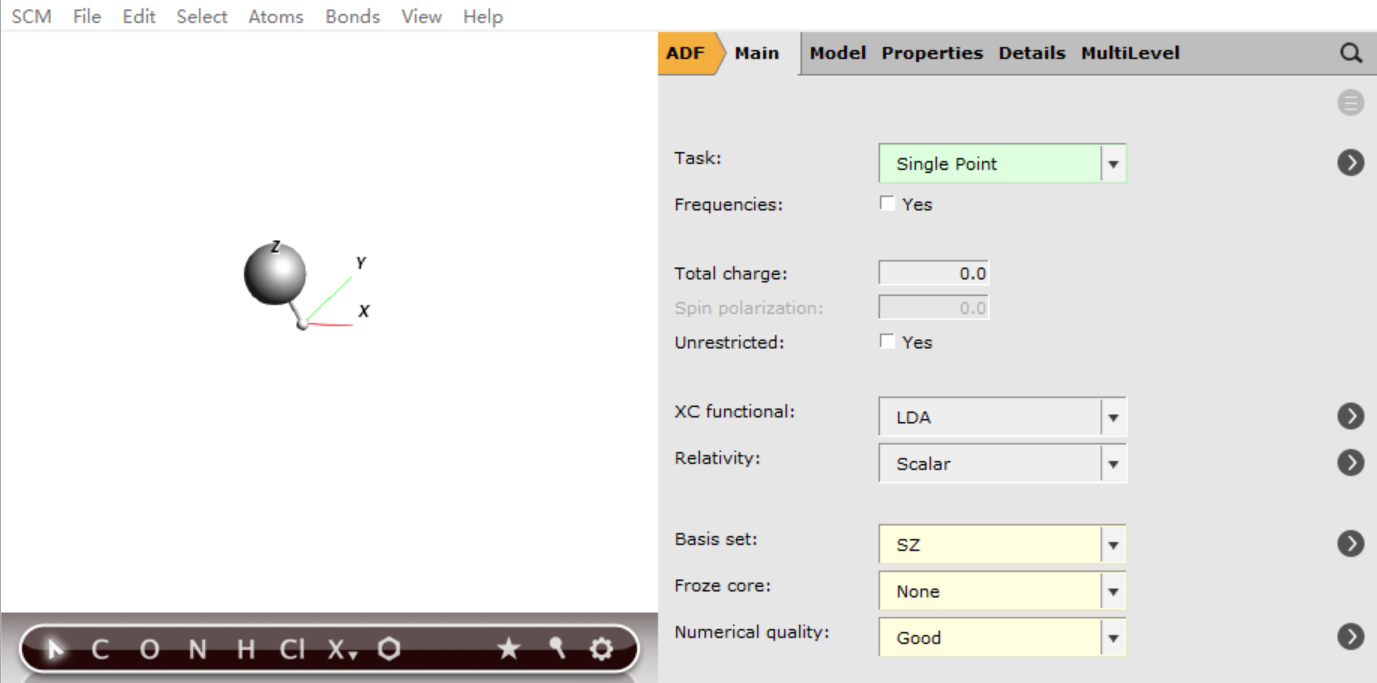
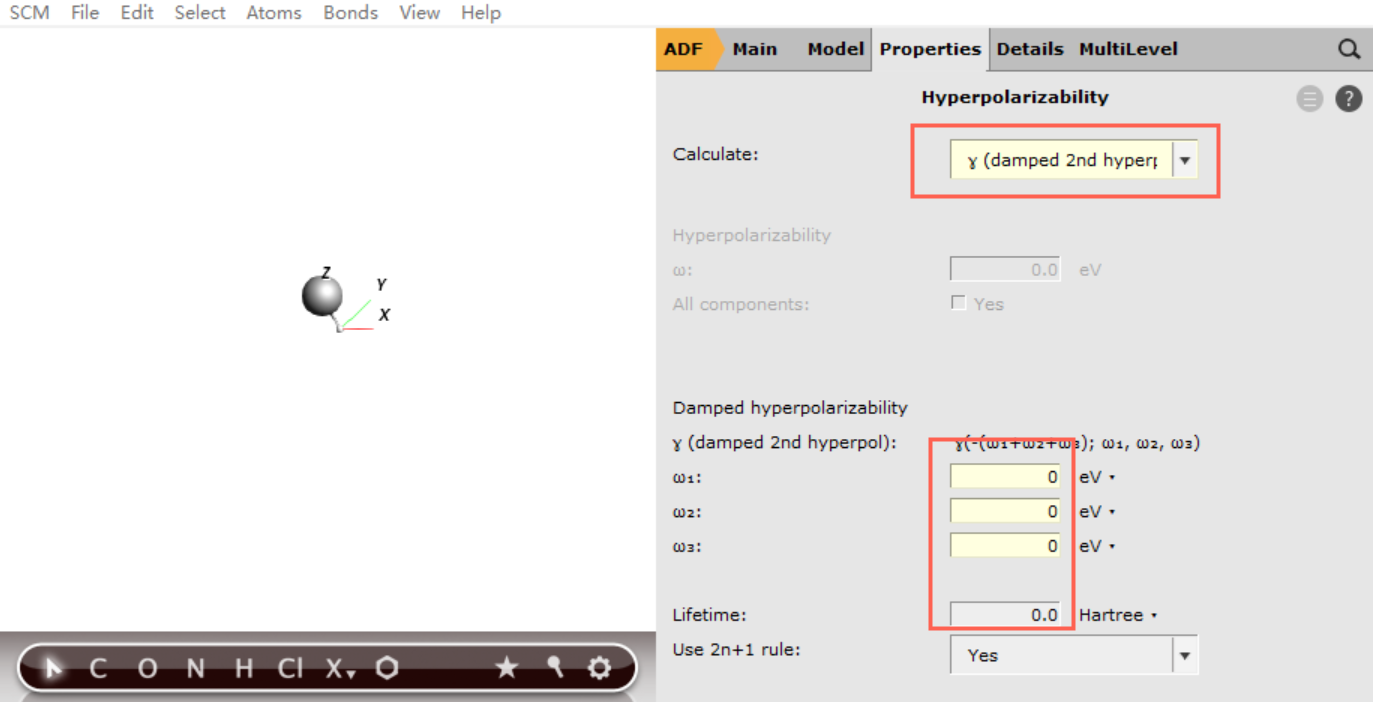
本文旨在比较各种计算方法。作为一个最简单的入手案例,我们选择LiH分子。按照作者选取的泛函(LDA)、基组(SZ)、计算方法(Damped Cubic Response Theory,在GUI中对应Properties - Hyperolarizability - Calculate - γ(damped 2nd hyperpol),选择该选项会同时计算α、β、γ),频率($ω_1$、$ω_2$、$ω_3$、liftime均为0,因为计算的是静态超极化率)。
参数设置
模型
Li-H键长1.60埃,H-Li方向设置为z轴(依次选中H、Li,Edit - Align - With z-Axis).
参数
由于计算的是静态超极化率,因此lifetime、$ω_1$、$ω_2$、$ω_3$均设置为0。如果计算动态极化、超极化,设置相应的频率、寿命即可。具体可以参考:计算动态超极化率、双光子吸收截面TPA Cross Section
如果是动态超极化率,激发态的寿命是用一个常见的现象学阻尼参数来近似的。这个值最好通过拟合分子的吸收数据来获得,不过这个值在相似的分子之间变化不大,因此估计值并不困难。文献“Journal of Chemical Physics 123, 174110 , 2005”中使用了0.004 Hatree。
保存并提交任务。
注意:这篇文章仅仅是为了测试对比不同的方法,因此我们真正计算的时候,可以考虑更精确的泛函、更大的基组(参考:ADF参数设置详解)。Numerical Quality建议设置为Good。
结果查看
偶极矩
SCM - Output,窗口底部输入dipole moment回车搜索得到:
Dipole Moment *** (Debye) *** Vector : 0.00000000 0.00000000 4.67430075 Magnitude: 4.67430075
因此得到偶极矩,因为设置H-Li为Z轴,因此偶极矩只有z方向有分量。
极化率
极化率α是一个二阶张量,搜索 Polarizability tensor:
THE DIPOLE-DIPOLE POLARIZABILITY TENSOR:
FREQUENCY CYCLE NR.: 1 AT 0.0000000000 HARTREES
Y Z X
20.582595 0.000000 0.000000
0.000000 8.341782 0.000000
0.000000 0.000000 20.582595
FREQUENCY CYCLE NR.: 2 AT 0.0000000000 HARTREES
Y Z X
20.582595 0.000000 0.000000
0.000000 8.341782 0.000000
0.000000 0.000000 20.582595
FREQUENCY CYCLE NR.: 3 AT 0.0000000000 HARTREES
Y Z X
20.582595 0.000000 0.000000
0.000000 8.341782 0.000000
0.000000 0.000000 20.582595
这里分别列出了三次迭代的极化率的实部与虚部结果(看最后一个即可),各自都是3*3的矩阵,分别对应$α_{ij}$,其中i,j=y,x,x。 可以看到
- $α_{xx}$=20.5826 a.u.
- $α_{zz}$=8.34178 a.u.
与文献中20.59、8.21一致。
一阶超极化率β
在out窗口,搜索 Hyperpolarizability tensor:
The STATIC hyperpolarizability tensor beta Non-zero components of beta: beta(z z z ) = -360.95 -180.47 -0.31183E-29 -0.15592E-29 beta(y z z ) = -0.11166E-06 -0.55830E-07 -0.96466E-39 -0.48233E-39 beta(x z z ) = 0.11461E-06 0.57307E-07 0.99017E-39 0.49508E-39 beta(z y z ) = -0.11166E-06 -0.55830E-07 -0.96466E-39 -0.48233E-39 beta(y y z ) = -345.05 -172.53 -0.29810E-29 -0.14905E-29 beta(z x z ) = 0.11461E-06 0.57307E-07 0.99017E-39 0.49508E-39 beta(x x z ) = -345.05 -172.53 -0.29810E-29 -0.14905E-29 beta(z z y ) = -0.11166E-06 -0.55830E-07 -0.96466E-39 -0.48233E-39 beta(y z y ) = -345.05 -172.53 -0.29810E-29 -0.14905E-29 beta(z y y ) = -345.05 -172.53 -0.29810E-29 -0.14905E-29 beta(z z x ) = 0.11461E-06 0.57307E-07 0.99017E-39 0.49508E-39 beta(x z x ) = -345.05 -172.53 -0.29810E-29 -0.14905E-29 beta(z x x ) = -360.95 -172.53 -0.29810E-29 -0.14905E-29
这里同样地列出了β张量的实部与虚部。β是三阶张量,有三个下标$β_{ijk}$,i,j,k=x,y,z。其中
- $β_{zxx}$ = -345.05 a.u.
- $β_{zzz}$ = -360.9820 a.u.
与文中结果大致一致,实际上与Dalton的结果更接近。不同版本的ADF计算方法也不同,尤其是2016到2019每个版本之间均有较大调整。
二阶超极化率γ
在out中搜索Second hyperpolarizability tensor:
Second hyperpolarizability tensor:
X Y Z
X X X -4238.9431 0.0000 0.0001
Y 0.0000 -1426.0317 0.0000
Z 0.0000 0.0000 9904.3713
X Y X 0.0000 -1426.0317 0.0000
Y -1426.0317 0.0000 0.0000
Z 0.0000 0.0000 0.0000
X Z X 0.0000 0.0000 9904.3713
Y 0.0000 0.0000 0.0000
Z 9904.3713 0.0000 -0.0001
Y X X 0.0000 -1426.0317 0.0000
Y -1426.0317 0.0000 0.0000
Z 0.0000 0.0000 0.0000
Y Y X -1426.0317 0.0000 0.0000
Y 0.0000 -4238.9431 0.0001
Z 0.0000 0.0001 9904.3713
Y Z X 0.0000 0.0000 0.0000
Y 0.0000 0.0000 9904.3713
Z 0.0000 9904.3713 -0.0001
Z X X 0.0000 0.0000 9904.0350
Y 0.0000 0.0000 0.0000
Z 9904.0350 0.0000 -0.0001
Z Y X 0.0000 0.0000 0.0000
Y 0.0000 0.0000 9904.0350
Z 0.0000 9904.0350 -0.0001
Z Z X 9904.0350 0.0000 -0.0001
Y 0.0000 9904.0350 -0.0001
Z -0.0001 -0.0001 29981.6352
----------------------------------------------------
IMAGINARY SECOND HYPERPOLARIZABILITY
----------------------------------------------------
X Y Z
X X X 0.0000 0.0000 0.0000
Y 0.0000 0.0000 0.0000
Z 0.0000 0.0000 0.0000
X Y X 0.0000 0.0000 0.0000
Y 0.0000 0.0000 0.0000
Z 0.0000 0.0000 0.0000
X Z X 0.0000 0.0000 0.0000
Y 0.0000 0.0000 0.0000
Z 0.0000 0.0000 0.0000
Y X X 0.0000 0.0000 0.0000
Y 0.0000 0.0000 0.0000
Z 0.0000 0.0000 0.0000
Y Y X 0.0000 0.0000 0.0000
Y 0.0000 0.0000 0.0000
Z 0.0000 0.0000 0.0000
Y Z X 0.0000 0.0000 0.0000
Y 0.0000 0.0000 0.0000
Z 0.0000 0.0000 0.0000
Z X X 0.0000 0.0000 0.0000
Y 0.0000 0.0000 0.0000
Z 0.0000 0.0000 0.0000
Z Y X 0.0000 0.0000 0.0000
Y 0.0000 0.0000 0.0000
Z 0.0000 0.0000 0.0000
Z Z X 0.0000 0.0000 0.0000
Y 0.0000 0.0000 0.0000
Z 0.0000 0.0000 0.0000
同样列出了二阶超极化率的实部与虚部。γ为四阶张量,因此有四个下标$γ_{ijkl}$,i,j,k,l=x,y,z。其中:
- $γ_{xxxx}$ = -4238.9431 a.u.
- $γ_{xxyy}$ = -1426.0317 a.u.
- $γ_{xxzz}$ = 9904.3713 a.u.
- $γ_{zzzz}$ = 29981.6352 a.u.