使用 QuantumATK 研究能带结构和态密度
概述
能带和态密度是块体材料电子态的基本属性,也是最常用的计算之一,对了解材料的特性非常重要。QuantumATK支持多种计算:
- 能带(BandStructure)
- 态密度(DensityOfStates)
- 投影能带(FatBandStructure)
- 投影态密度(ProjectedDensityOfStates)
QuantumATK支持将能带和态密度进行复杂的投影计算和交互式分析,使用方便。用户可以使用图形界面直接将能带和DOS投影到:
- 每种元素
- 每种元素的壳层、轨道
- 每个原子
- 自旋分量(Up/Down,x/y/z)
- 用户指定的原子组合(任意原子标签Tag)
提示
本教程使用特定版本的QuantumATK创建,因此涉及的截图和脚本参数可能与您实际使用的版本略有区别,请在学习时务必注意。
完整视频演示
- 能带、态密度、投影能带和投影态密度快速视频演示
- 全屏播放更清晰
能带和态密度的计算
基本计算设置
- 构建好材料结构模型后,点击右下角“箭头”图标发送至Script Generator;
- 添加New Calculator,设置合适的计算方法;
- 添加Analysis – Band Structure,修改合适的高对称点路径、每段能带的点数、费米面以上的能带数;
- 添加Analysis – DensityOfStates,设置较多的k点;
- 添加Analysis – Fat Bandstructure,可以计算投影能带;
- 打开FatBandStructure,选择Projection on “Element” 或者 “Element and Shell” 或“Element and orbital”;
- 其他设置与能带计算计算类似;
- 添加Analysis – ProjectedDensityOfStates,可以计算投影态密度;
- 打开ProjectedDensityOfStates,选择Projection on “Element” 或者 “Element and Shell” 或“Element and orbital”;
- 其他设置与态密度计算计算类似;
将脚本发送到 Job Manager 执行,稍等片刻即可在主窗口中的LabFloor中看到计算结果(选定输出的hdf5文件)。
演示视频:能带与密度计算设置
布里渊区和能带计算使用的高对称点
VNL中默认的高对称点的标志依赖于晶格的布拉维格子种类,在Builder中
- 可以通过Crystal Symmetry Info查看体系的对称性;
- 使用 Brillouin Zone Viewer 查看这些高对称点在布里渊区里的位置;
- 如果发现体系的格子属性不对,导致无法设置需要的高对称点,则可以在Lattice Parameters…里调整格子,也有可能需要重新优化结构;
自定义k点路径
QuantumATK计算中还支持用户自定义任意布里渊区路径,这通过kpoints参数实现(见下面脚本)。需要注意以下两点:
- 使用
kpoints,必须删去route和points_per_segment; - kpoints不能只定义线段两端,而必须逐点定义所有线段上的点。
# ------------------------------------------------------------- # Bandstructure # ------------------------------------------------------------- bandstructure = Bandstructure( configuration=bulk_configuration, kpoints=[[0.0,0.0,0.0],[0.0,0.0,0.1],[0.0,0.0,0.2],[0.0,0.0,0.3],[0.0,0.0,0.4],[0.0,0.0,0.5]], bands_above_fermi_level=All )
能带和态密度的结果分析与作图
能带与投影能带分析工具
NanoLab 提供了方便的能带分析工具(主窗口右侧Band Structure Analyzer),用户可以:
- 直接作图、查看能带结构;
- 在能带上进行交互式测量;
- 自定义坐标轴、标签、标题、线型、粗细、颜色、字号等所有的图像特性;
- 在图像上添加箭头和文字标记;
- 直接给出直接和间接带隙;
- 导出高质量的pdf、png、eps等图像格式;
- 导出原始数据进行分析和作图。
在投影能带(FatBandStructure)的计算结果分析(主窗口右侧 Fat Band Structure Analyzer)中,用户可以:
- 方便的选择要显示的投影能带和颜色。
- 选择投影的显示方式:带权重的线、圆点、带权重的圆点
- 与能带类似自定义图像特性。
视频演示:能带与投影能带作图
态密度分析工具
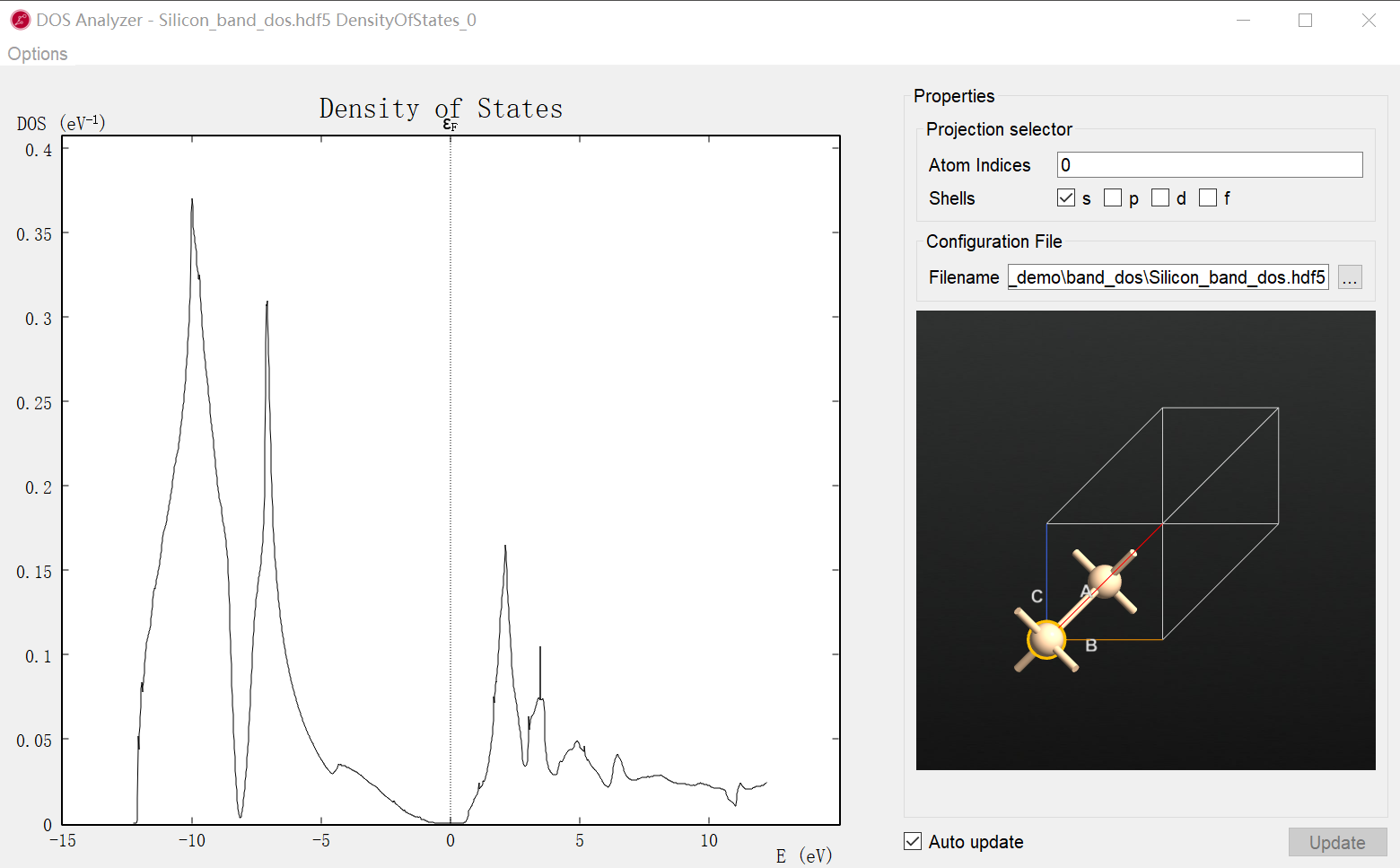
- 使用DOS Analyzer可以直接查看态密度计算结果。即使不进行高级的投影能带计算,仅就DOS结果也可以进行简单的投影分析。
- 我们推荐2017版开始提供的全功能PDOS分析计算工具,功能更全面、使用更便捷、作图更精美。详见视频演示和下文介绍。
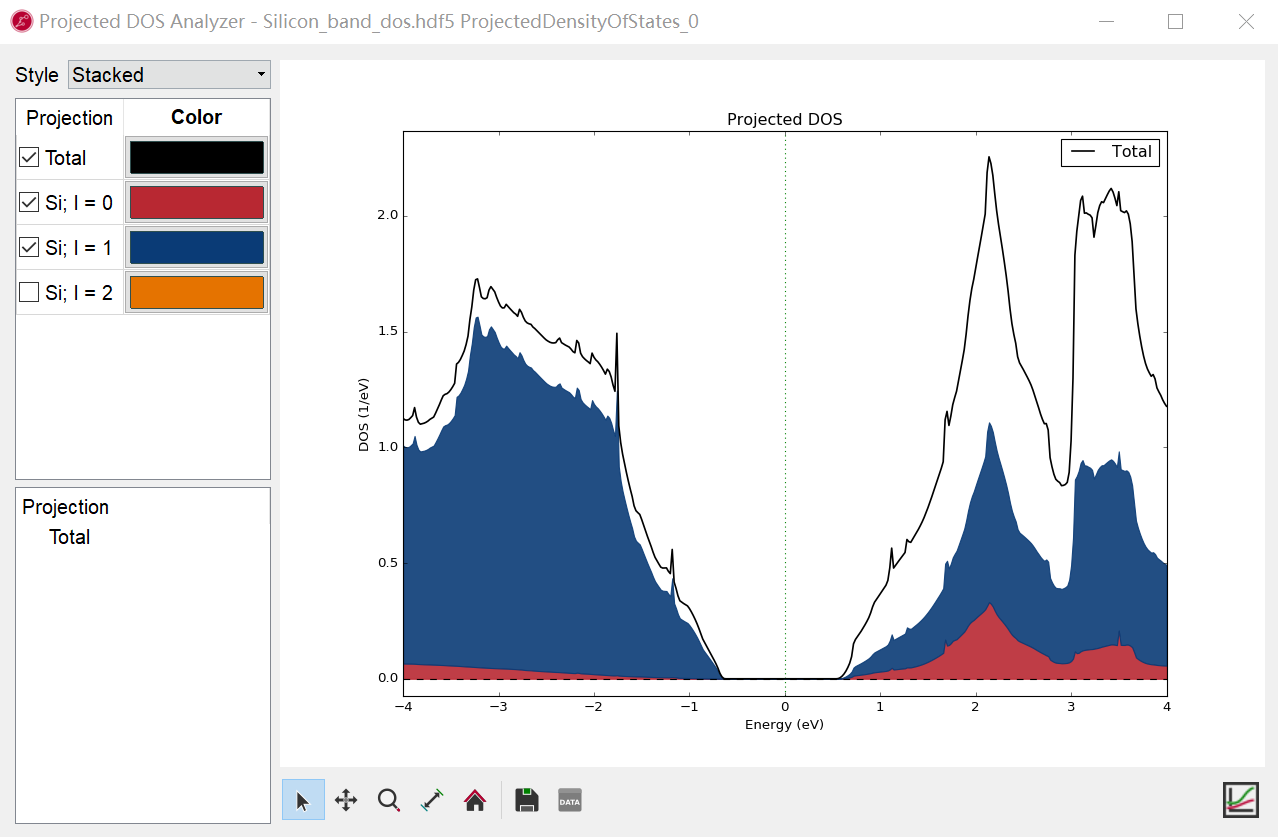
投影态密度(ProjectedDensityOfStates)分析工具
从2017版开始,QuantumATK开始支持全功能的态密度投影(ProjectedDensityOfStates)。与能带投影一样用户可以使用便捷的图形界面直接将 DOS 投影到:
- 每种元素
- 每种元素的壳层、轨道
- 每个原子
- 自旋分量(Up/Down,x/y/z)
- 用户指定的原子组合(任意原子标签Tag)
在计算结果中,用户可以方便的选择要显示的方式。显示方法则有三种模式:线状图(Line)、堆积图(Stack)、填充图(Fill)。
视频演示:态密度与投影态密度作图
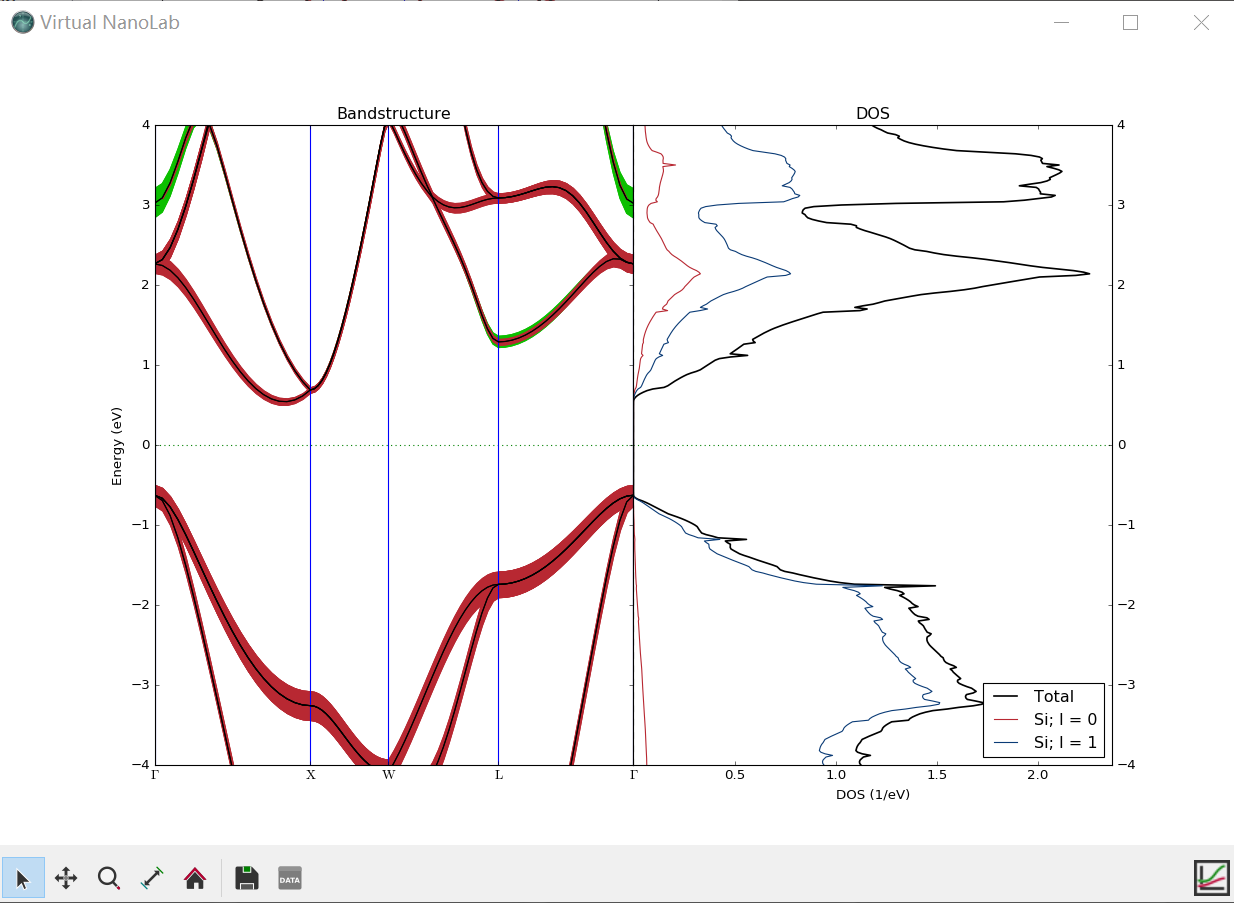
能带与态密度组合作图
QuantumATK 的图形界面很方便的将能带(或投影能带)和投影态密度态密度进行组合作图,同步的进行交互式分析。同时打开能带和投影态密度的显示窗口,拖动投影态密度窗口右下角的图标,将其放置在能带(或投影能带)上,选择“BS/DOS”作图即可。
视频演示:能带与态密度组合作图
导出图像、查看原始数据
QuantumATK支持直接导出png、jpg、eps、pdf等多种图像格式文件,也可以直接查看原始数据文本。
视频演示:导出图像、查看原始数据
进一步调整作图效果
- 使用plt脚本可以进一步调整作图效果,详见:plt 作图脚本与应用实践。
定义
投影能带
投影能带(projected band structure)又称为 fat band structure,是一种可视化不同的轨道对能带的贡献的方法,该方法的原理是计算每个本征值对给定投影子空间的权重。计算方法如下:本征态和本征值由通常的能带方法求得,即求解如下的本征方程: $$ H \psi_{n {\bf k}} = E \psi_{n {\bf k}}。 $$
接下来定义在子空间 $M$ 上的投影算符 ${\hat{\bf P}_M}$,得到$(E_{n {\bf k}}, \psi_{n {\bf k}})$ 的权重 $\omega^{M}_{n {\bf k}}$ 为
$$ \omega^{M}_{n {\bf k}} = \langle \psi_{n {\bf k}} | \hat{\bf P}_M | \psi_{n {\bf k}} \rangle $$
该权重满足波函数 $\psi_{n {\bf k}}$ 的归一化条件。
投影态密度(ProjectedDensityOfStates)
投影态密度是一种可视化不同的轨道对态密度贡献的方法。由态密度的定义: $$ D(\epsilon) = \sum_{n} \delta \left(\epsilon - \epsilon _{n} \right) $$
可以使用在子空间 $M$ 上的投影算符 ${\hat{\bf P}_M}$ 得到投影态密度为
$$ D _{M}(\epsilon) = \sum_{n} \delta \left(\epsilon - \epsilon _{n} \right) \langle \psi_{n} | \hat{\bf P}_M | \psi_{n } \rangle$$
$\psi_{n}$ 为波函数。
参考
- 实例教程:计算晶体能带
- 投影算符的定义:Projection、ProjectionGenerator