关键词：迁移率，电声耦合（电子-声子相互作用），温度相关载流子输运性质，电导率（conductivity），畸变势（deformation potential）

在本教程中吗，我们将介绍如何计算石墨烯（graphene）中的声子限制的电子迁移率。结合电子态和玻尔兹曼输运方程，同时考虑声子模式与电子-声子相互作用，使用 DFT 方法计算电子迁移率。我们将使用 QuantumATK 新版中提供的分析模块 ElectronPhononCoupling，DeformationPotential 和 Mobility 功能来完成。

计算迁移率 $\mu$ 的关键是计算电子的弛豫时间 $\tau$。弛豫时间有两种计算方法：

1. 全角度(k,q)-相关：这种方法完整的考虑 $\tau$ 对电子和声子的波矢 $\mathbf{k}$ 和 $\mathbf{q}$ 的相关，即 $\tau=\tau(\mathbf{k},\mathbf{q})$。下面称为(k,q)-相关方法。
2. 各向同性散射：这种方法仅考虑能量有关的 $\tau=\tau(E)$，假定 $\tau(E)$ 在动量空间中的变化是各向同性的。下面称为E-相关方法。

下面的计算表明，两种方法得到的结果相差无几，但是第二种方法比第一种方法计算速度大大提高。

文末将介绍理论背景知识和更多相关信息，已发表结果参见[GMSB16]。

在 Builder 中添加一个石墨烯结构：

• Add → Database → 搜素 “Graphene”

设置晶格常数C方向为20 Å：

• Bulk Tools → Lattice parameters, c=20Å

将结构在视图中居中（Coordinate Tools → Center → Apply），发送至脚本生成器Script Generator。

要进行精确的弛豫时间和迁移率计算，首先要精确的优化A、B方向的晶格常数并计算能带。

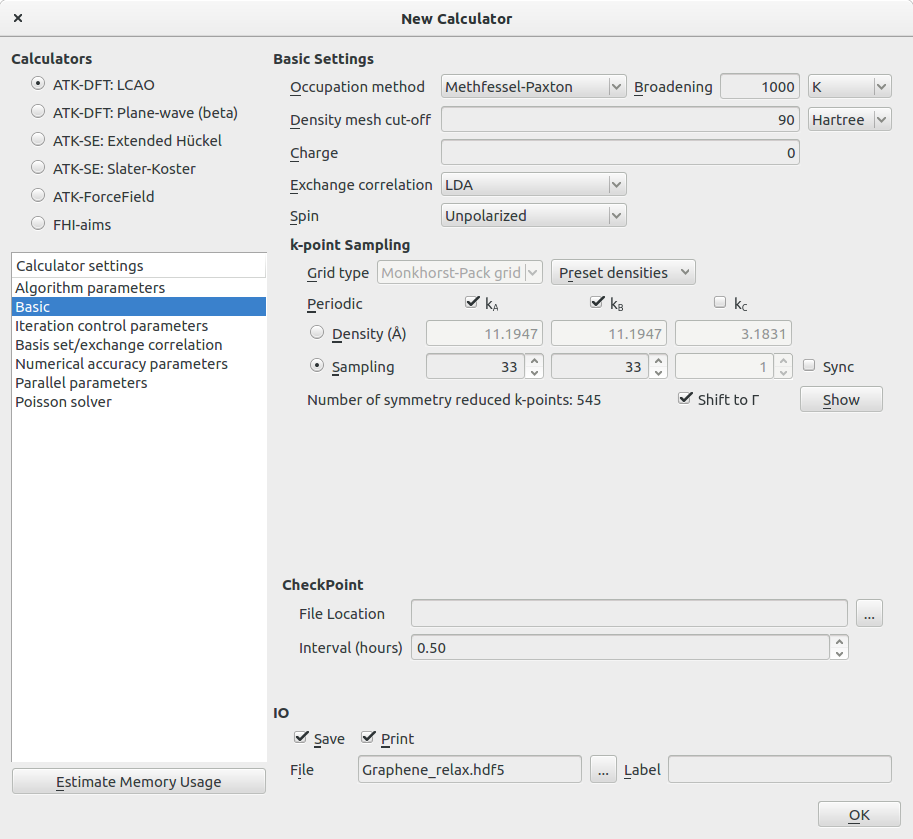
• 新增一个 New Calculator
  • 设置 Opcupation methond 为 Methfessel-Paxton
  • 设置 K-point sampling：kA=33,kB=33,kC=1
  • 设置 Density mesh-cutoff 为 90 Ha

• 点击 Optimization，增加一个 OptimizeGeometry 模块，按如下设置参数：
  • 最大受力 Force Tolerance 为 0.001eV/Å
  • 取消勾选Constrain Lattice Vectors 后面的 x 和 y

• 添加 Analysis → Bandstructure
  • 设置 Points per segment 为 100
  • 设置 Brillouin Zone route 为 G, K, M, G
• 设置默认输出文件名 Default output file: graphene_relax.hdf5
• 发送脚本到任务管理器 Job manager，运行计算任务

计算结束后，点击 LabFloor 中包含在 Graphene_relax.hdf5 的 Bandstructure 图标，使用右侧的 Bandstructure Analyzer 可以查看能带图。

将鼠标防止在一条能带上就可以看到相关的信息。比如上图中高亮的一条价带的编号为3，导带为4。这两条能带是与迁移率有关的关键能带，接下来我们将专注于这两条能带。

下面我们将计算石墨烯的动力学矩阵（dynamical matrix）。由动力学矩阵，可以得到声子谱和振动模式，从而可以测验计算的精确度。

步骤如下：

• 打开 LabFloor 中的 graphene_relax.hdf5 文件，发送弛豫后的原子结构文件（gID001）到脚本生成器 Script generator，进行如下设置：
• 设置 K 点网格：kA=3,kB=3,kC=1。
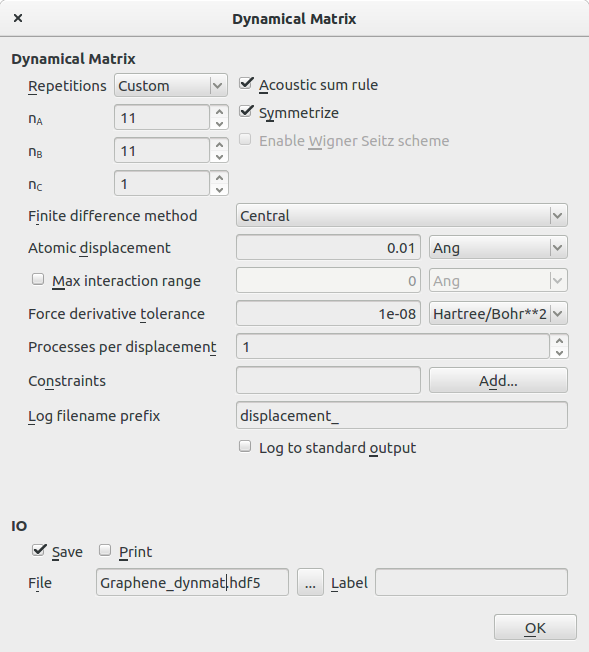
• 添加 Analysis → DynamicalMatrix 模块，设置参数如下：
  • 选择 Repetitions 为 Custom
  • 设置 nA=11,nB=11,nC=1

• 添加 Analysis → PhononBandstructure，设置如下参数：
  • Points per segment：100
  • Brillouin zone route：G,M,K,G

在 Sciprt Generator 主面板中，将 Default output file 改为：Graphene_dynmat.hdf5，脚本发送到 Job Manager，保存输入文件Graphene.py，完成计算。

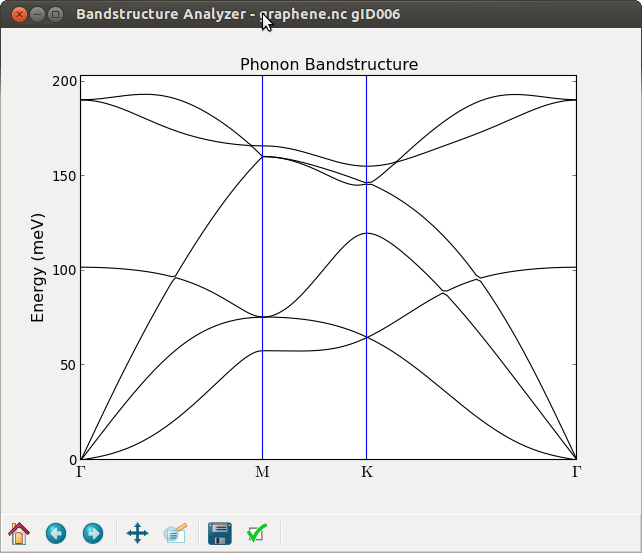
计算结束后，使用 Bandstructure Analyzer 查看声子谱结构，如下：

接下来，我们来看如何计算石墨烯中的电子迁移率。在已经计算的电子态结构和动力学矩阵的基础上，要计算迁移率还需要三步：

1. 计算哈密顿量导数
2. 计算电子-声子耦合
3. 计算迁移率

其中第2、第3步分别有(k,q)-相关方法和E-相关方法两种，下文分别介绍。

为了计算电子-声子耦合，需要首先计算哈密顿量的一阶偏微分。哈密顿量对第 $i$ 个原子的笛卡尔坐标$\alpha$的一阶偏微分，$\partial \hat{H}/ \partial R_{i,\alpha}$，可以使用 HamiltonianDerivatives 对象计算得到。

现在，按下面步骤操作：

• 打开 LabFloor 中的 graphene_relax.hdf5 文件，发送弛豫后的原子结构文件（gID001）到脚本生成器 Script generator。
• 在 New Calculator，设置 K 点网格：（3,3,1）
• 添加 Analysis → HamiltonianDerivatives 模块，设置 nA=11，nB=11，nC=1.
• 设置默认输出文件名Default output file: graphene_dHdR.hdf5

发送任务到任务管理器 Job manager，保存输入文件graphene_dHdR.py，运行计算任务。

现在，我们已得到计算电子-声子耦合性质的要素：1）动力学矩阵；2）哈密顿量微分。首先，我们将在倒空间沿特定方向拟合形变势。然后，在 q 网格中计算电子-声子耦合，及声学声子极限下的迁移率。

首先，为得到声学模的形变势，我们考虑电子-声子耦合矩阵元随q的变化关系，$|M_{\mathbf{k},\mathbf{q}}^\lambda|$，操作如下：

• 打开 LabFloor 中的 graphene_relax.nc 文件，发送弛豫后的原子结构文件（gID001）到脚本生成器 Script generator。
• 添加分析器Analysis → DeformationPotential，

当添加 DeformationPotential 模块，DynamicalMatrix 和 HamiltonianDerivatives 将被自动添加到脚本生成器中，得到如下：

查看计算器 Calculator 中 k-point 取 (7,7,1)，而不是计算动力学矩阵和哈密顿量微分时使用的 k 点 (1,1,1)。

现在，打开 DeformationPotential，首先设置电子初态的 k-point，设置如下：

• 初始设置k-point = K。在K点（狄拉克点，Dirac point）右侧，导带和价带简并
• 设置 k-point = Other(Fractional)
• 设置 a = b = 0.33334

K点右侧价带（valence band, VB）和导带（conduction band, CB）简并。这表明，任何两个态的线性组合都是电子本征态。由于价带和导带有不同的对称性，他们耦合为不同的声子。波矢稍稍偏离 K 点时，我们假设为纯价带和纯导带。

下面，需要指定考虑的声子 q 点值。大多情况下，我们对决定形变势和迁移率的小$|q|$值感兴趣。我们可以通过由一个初始 q 点和方向矢量来确定一条线上的 q 点值。初始 q 点和方向矢量由分数坐标给出。我们可以选取布里渊区的一个路径。使用前面的参数：

• 保持 First point 为 $\Gamma$ 点
• 设置方向矢量：a, b, c = (0.1, 0, 0)
• 设置每段的 q 点数：20
• 设置电子能带：3，4

再增加一个 DeformationPotential 对象，其他参数一样，除

• 方向矢量：a, b, c = (0.1, 0.1, 0)

• 设置默认输出文件名 Default output file: graphene.nc

由于我们已计算了动力学矩阵和哈密顿量微分，不必再重新计算，直接从文件读取数据即可。发送脚本到编辑器 Editor，并替换 Dynamical Matrix 和 Hamiltonian Derivatives 部分如下：

# -------------------------------------------------------------
# Dynamical matrix
# -------------------------------------------------------------
dynamical_matrix = nlread('graphene.nc', DynamicalMatrix)[0]
 
# -------------------------------------------------------------
# Hamiltonian derivatives
# -------------------------------------------------------------
hamiltonian_derivatives = nlread('graphene.nc', HamiltonianDerivatives)[0]

发送计算任务至任务管理器 Job manager 并运行计算任务。任务耗时几分钟完成。

计算完成后使用 Deformation Potential Analyzer 分析器可视化 LabFloor 中的计算结果文件 graphene.nc。两张图分别显示了所选模式的声子能量随 $|q|$（上图）和电子-声子耦合矩阵元随 $|q|$（下图）的变化规律。图的下部显示有一些分析选项。可以选择如下：

• 初始和最终电子能带的指标
• 声子模式
• 耦合矩阵类型，unscaled 或 scaled
• 线性拟合区间

在 Fitting output 下方显示线性拟合结果，零阶、一阶形变势，以及线性拟合的质量。

试着改变不同的电子能带、声子模式、拟合区间，看看有什么变化。对比各 DeformationPotential 对象，q 取沿 (0, 0, 0)→(0.1, 0.1, 0)方向。分析计算数据，得到如下结论：

• 平面外声子模式（0）与电子价带（3）、导带（4）均不耦合。
• 在小 q 值处，声子模式 1 和 2（LA 和 TA）呈线性规律，表示一阶形变势模型的准确性。但是，拟合形变势值取决于特定的 q 方向。简化形变势近似中，假设球对称性，并由 q 决定，因此，应使用合适的平均形变势值。
• 尽管应考虑更多的方向来得到精确的期望值，TA 和 LA 声子模式的一阶形变势值仍在 2-5eV 区间内。
• LO 和 TO 光学模式（4,5）接近常数，用零阶形变势模型描述基本正确。

为更精确研究形变势随角度的变化，尝试下面的步骤：

• 退回到前面计算形变势的 python 脚本
• 删除最后的 DeformationPotential 模块
• 修改脚本中的 Deformation 部分的程序行，将下面的程序语句：

# -------------------------------------------------------------
# Deformation potential
# -------------------------------------------------------------
q_0 = numpy.array([0, 0, 0])
q_direction = numpy.array([0.1, 0, 0])
points_per_segment = 20
q_path = [list(q_0 + s*q_direction) for s in numpy.linspace(0, 1, points_per_segment)]

替换为：

# -------------------------------------------------------------
# Deformation potential
# -------------------------------------------------------------
# Load function to convert from cartesian to fractional coordinates.
from NL.CommonConcepts.Configurations.Utilities import cartesian2fractional
 
# Radius of circle, in units of Ang^-1.
q_norm = 0.01
thetas = numpy.linspace(0,numpy.pi*2,60)
 
# Setup list of cartesian q-points in a circle.
q_circle_cartesian = [[q_norm*numpy.cos(t), q_norm*numpy.sin(t), 0] for t in thetas]*Ang**-1
 
# Get the reciprocal lattice vectors.
reciprocal_vectors = bulk_configuration.bravaisLattice().reciprocalVectors()
 
# Convert q-point to fractional.
q_path = cartesian2fractional(q_circle_cartesian, reciprocal_vectors)

首先设置笛卡尔坐标系下圆形的一系列 q 点，然后转化为 q 点的分数坐标。运行脚本，查看 DeformationPotential 对象，如下图所示为初始能带和最终能带均为 4，声子模指标为 2（LA 模）的情况。电子-声子耦合矩阵元显示出明显的震荡。平均值接近 0.04 eV/Å。由于 q 圆的半径为0.01 $Å^{-1}$，一阶形变势平均值 $D^{(1)}$ 为 4eV，与文献 [KTJ12b] 报道一致。

DeformationPotential对象中包含了计算迁移率所需的一些信息，即电子-声子耦合项。但是，为计算弛豫时间和迁移率，我们需要知道初始 k 值构成的有限 q 网格下的耦合项。这是由 ATK 中 ElectronPhononCoupling 分析对象处理的。

下面将使用两个 ElectronPhononCoupling 对象。首先，计算 k 空间中完整 q 网格下沿一条线上的耦合元，用来分析 ($q_x$, $q_y$) 点的耦合矩阵元，及特定能量和温度下的弛豫时间的计算。操作如下：

• 打开 LabFloor 中的 graphene_relax.nc 文件，发送弛豫后的原子结构文件（gID001）到脚本生成器 Script generator。
• 添加分析器 Analysis → ElectronPhononCoupling

我们要计算 Δ 连线（由原点至 K 点）上 k 点的电子-声子耦合。笛卡尔坐标系中，K 点坐标为(1.69044, 0, 0)，可以由电子能带结构Bandstructure 对象中得到该信息，即在 LabFloor 中点击 Text Representation。现在，打开 ElectronPhononCoupling 对象，设置如下：

• 自定义 k 网格，k grid = Custom（Cartesian）
• 自定义 q 网格，q grid = Custom（Cartesian）
• 电子能带，Electron bands = 3, 4
• 声子模式，Phonon modes = 1, 2（我们仅关注声学模）

运行计算前，发送脚本至编辑器 Editor，用下面的程序语句替换动力学矩阵和哈密顿量微分部分的语句：

# -------------------------------------------------------------
# Dynamical matrix
# -------------------------------------------------------------
dynamical_matrix = nlread('graphene.nc', DynamicalMatrix)[0]
# -------------------------------------------------------------
# Hamiltonian derivatives
# -------------------------------------------------------------
hamiltonian_derivatives = nlread('graphene.nc', HamiltonianDerivatives)[0]

运行计算前，注意：

当计算结束后，使用Electron-Phonon Coupling Analyzer分析器可视化结果。显示如下图的窗口：

电子-声子耦合分析工具提供了丰富的信息，在工具窗口左侧你可以设置一些输入的参数用于作图：

• Electron-Phonon Coupling Analyzer 分析器包含很多信息。窗口左侧设置绘制图的输入参数：
• Initial k-point 和 Initial band 指标。“Initial State Properties” 栏下显示了对应 k 点和能量。
• Final band，决定您是否考虑了能带内或能带间散射。
• Phonon mode，声子模式指标。
• Coupling matrix，可设置为 “scaled”或“unscaled”, 与 Deformation Potential 中的定义一样，参见上文。
• Energy broadening，此参数决定了绘图窗口中$\delta$-函数的展宽。$\delta$-函数在程序中用 Lorentzian 函数 $\delta(E)\approx \frac{1}{2\pi}\frac{\Gamma}{\Gamma^2 + E^2}$。能量展宽决定了 $\Gamma$ 的值。取较小的能量展宽，将会得到较窄的$\delta$-函数。q 网格优化的设置限制了能够取多小的值。
• 最后，通过 Refinement 参数设置优化 q 点网格。因此，如果最初进行了 (20, 20, 1) q 网格的计算，通过设置 Refinement = 2 可以得到 (40, 40, 1) q 网格。所有与 q 有关的性质，在新的 q 网格中可以线性插值得到。增加 Refinement 可以使您选择更小的能量展宽值。

Electron-Phonon Coupling Analyzer 中作图的所有物理量均以 $q_x$ 和 $q_y$ 为自变量。上面一行画出声子能量（左图），吸收声子的终态电子能量 $E_{k+q}$（中图），产生声子的终态电子能量 $E_{k-q}$（中图）。下面一行画出电子-声子耦合矩阵元（左图），吸收（中图）和发射（右图）声子的能量守恒 $\delta$-函数。

尝试调整绘图参数查看作图。

在开始迁移率计算之前，我们需要查看 Electron-Phonon Coupling Analyzer 中的：

• q-区间选取是否足够大？$\delta$-函数图中的环应被完全覆盖，而不是仅显示部分环。否则将不能覆盖散射相关的q区间。需要注意的是，通过改变初态的k指标，我们可以改变$\delta$-函数图中环的大小和形状。这是因为石墨烯布里渊区狄拉克点（Dirac cones）相应的发生移动。
• q 网格采样是否足够完备？鉴于计算迁移率时使用的温度（见下图），能量展宽通常应满足 $\Gamma < k_BT$。低温下，需要设置小的能量展宽和完备的 q 采样。无需重新计算电子-声子耦合，这个工作可以通过增加优化系数得到。

在计算实际迁移率之前，我们需要使用 Mobility 对象分析导带的弛豫时间 $\tau_{k,n}$随 $k$ 的变化关系。这在像石墨烯这样的二维材料中具有特别有趣的性质。根据 Bloch-Gruneisen 定理，由于相空间中的反向散射的减弱，弛豫时间在费米能级处显著增加。

• 打开 LabFloor 中的 graphene_relax.nc 文件，发送弛豫后的原子结构文件（gID001）到脚本生成器 Script generator。
• 添加分析器 Analysis → Mobility

打开 Mobility 对象，按照下图设置参数：

发送脚本到编辑器 Editor 中，删除上面 Mobility 部分的全部语句。这是由于使用已计算完成的数据，这部分就不需要了。添加下面的语句。

bulk_configuration = nlread('graphene.nc', BulkConfiguration)[1]
electron_phonon_coupling = nlread('graphene.nc', ElectronPhononCoupling)[0]
 
# -------------------------------------------------------------
# Mobility
# -------------------------------------------------------------
mobility = Mobility(
    configuration=bulk_configuration,
    electron_phonon_coupling=electron_phonon_coupling,
    temperature=10*Kelvin,
    phonon_modes=[1],
    fermi_shift=0.15*eV,
    energy_broadening=0.003*eV,
    refinement=15,
    )
nlsave('graphene_mobility.nc', mobility)

计算大约耗时 10-20 分钟。如此长的计算时间，是由于为精确描述低温下的情况，需要密的优化网格。迁移率计算完成后，使用下面的脚本可视化弛豫时间倒数随能量的变化。

import pylab as pl
 
mobility = nlread('graphene_mobility.nc', Mobility)[0]
 
# The phonon mode that should be considered.
mode = 1
 
# Get the inverse life time in ns^-1
gamma = mobility.inverseLifeTime().inUnitsOf(Second**-1)*1e-9
 
# Get the Fermi shift
fermi_shift = mobility.fermiShift()
 
# Get the eigenvalues at k.
e_k = mobility.eigenvaluesK().inUnitsOf(eV)
 
# Get Fermi level
Ef = mobility._fermiLevel().inUnitsOf(eV)
 
# Spin index
i_spin = 0
 
# Bloch state index. The electron-phonon coupling was calculated for bands 3 and 4. We look at 4, which has index 1.
i_bloch = 1
 
pl.figure(1)
pl.plot((e_k[i_spin, :, i_bloch] - Ef)/fermi_shift.inUnitsOf(eV), gamma[i_spin, mode, :, i_bloch], 'o-')
pl.xlabel('$\epsilon/\epsilon_F$', fontsize=14)
pl.ylabel('Inverse Life Time  (ns$^{-1})$', fontsize=14)
pl.legend(loc=0)
pl.xlim([0, 1.7])
pl.show()

图中弛豫时间倒数的下降（低散射率）对应费米能级处电子态满足 Bloch-Gruneisen 定理。二维系统中，低温下反向散射在相空间中被抑制，散射几率降低。这一效应的理论研究以前在其他二维电子气异质结[KS92]和类石墨烯材料[GMSB16], [HS08], [KTJ12], [KTJ12b]中也曾报道过。

为了计算迁移率，需要在石墨烯狄拉克点 $K$ 附近进行 k 点采样，因此，需要建立一个新的 ElectronPhononCoupling 对象。操作如下：

• 打开 LabFloor 中的 graphene_relax.nc 文件，发送弛豫后的原子结构文件（gID001）到脚本生成器 Script generator。
• 添加分析器 Analysis → ElectronPhononCoupling

打开ElectronPhononCoupling对象，设置如下图的参数：

运行计算前，将脚本发送至编辑器 Editor，用下面的语句替换 Dynamical Matrix 和 Hamiltonian Derivatives 段：

# -------------------------------------------------------------
# Dynamical matrix
# -------------------------------------------------------------
dynamical_matrix = nlread('graphene.nc', DynamicalMatrix)[0]
 
# -------------------------------------------------------------
# Hamiltonian derivatives
# -------------------------------------------------------------
hamiltonian_derivatives = nlread('graphene.nc', HamiltonianDerivatives)[0]

8 MPI 进程并行计算大约需要 2 小时完成计算任务。

计算完成后，按照下面步骤操作：

• 打开 LabFloor 中的 graphene_relax.nc 文件，发送弛豫后的原子结构文件（gID001）到脚本生成器 Script generator。
• 添加分析器 Analysis → Mobility

打开 Mobility 对象，按照下图设置参数：

发送脚本至编辑器，删除上面的 Mobility 语句，并添加下面脚本中前两行（剩下的部分是迁移率对象，与脚本中一致）。

bulk_configuration = nlread('graphene.nc', BulkConfiguration)[1]
electron_phonon_coupling = nlread('graphene.nc', ElectronPhononCoupling)[1]
# -------------------------------------------------------------
# Mobility
# -------------------------------------------------------------
mobility = Mobility(
            configuration=bulk_configuration,
            electron_phonon_coupling=electron_phonon_coupling,
            temperature=300*Kelvin,
            phonon_modes=All,
            fermi_shift=0.13*eV,
            energy_broadening=0.003*eV,
            refinement=1,
            )
nlsave('graphene.nc', mobility)

计算约耗时几秒钟。

计算完成后，打开 LabFloor 中的 graphene.nc 文件，找到迁移率对象，点击 Text Information 按钮。计算得到的电子迁移率$\approx 2 \times 10^5 cm^2/Vs$ 与文献报道的室温下电子迁移率 $n \approx 1 \times 10^{12} cm^{-2}$ 结果一致[KTJ12b]。 为得到石墨烯形变势的值，可以由 DFT 方法计算迁移率随温度的变化，然后通过（$\ref{7}$）式拟合得到。迁移率计算完成后，迁移率随温度变化关系的简单计算脚本如下：

plot_mu_t.py

# Load packages
from pylab import *
from scipy.optimize import curve_fit
 
# Read in the relaxed structure and the electron-phonon coupling
bulk_configuration = nlread('graphene_relax.nc', BulkConfiguration)[-1]
electron_phonon_coupling = nlread('graphene.nc', ElectronPhononCoupling)[-1]
 
# Define parameters for graphene
fermi_velocity = 1e6*Meter*Second**(-1)
sound_velocity = 14.1*1e3*Meter*Second**(-1)
mass_density = 7.6*1e-7*kiloGram*Meter**(-2)
fermi_shift = 130*meV
carrier_concentration = (130.0/11.65)**2*1e14*Meter**(-2)
 
# Analytical mobility as a function of temperature, see Eq. (7)
def f(temperature, D):
    """
    temperature: The temperature of the system with units of Kelvin.
    D          : The deformation potential. No unit, but values in eV.
    """
    mobility = 4*elementary_charge*hbar*mass_density*fermi_velocity**2*sound_velocity**2 / \
    (numpy.pi*carrier_concentration*boltzmann_constant*(temperature*Kelvin)*(D*eV)**2)
    # Return mobility in units of cm^2/Vs
    return mobility.inUnitsOf(Meter**2/(Volt*Second))*1e4
 
# Loop over temperatures and calculate the mobility
Ts = numpy.linspace(100.0, 300.0, 10)
mu_list = []
for T in Ts:
    temp=T*Kelvin
    # -------------------------------------------------------------
    # Mobility
    # -------------------------------------------------------------
    mobility = Mobility(
        configuration=bulk_configuration,
        electron_phonon_coupling=electron_phonon_coupling,
        temperature=temp,
        phonon_modes=[1],
        fermi_shift=fermi_shift,
        energy_broadening=0.003*eV,
        refinement=1,
        )
    mu_h,mu_e=mobility.evaluate()
    mu_list.append(mu_e.inUnitsOf(Meter**2/(Volt*Second))*1e4)
 
# Plot the data
plot(Ts,mu_list,'-o' )
 
# Fit the data
D,tmp = curve_fit(f,Ts, mu_list)
 
# Plot the fit
plot(Ts,f(Ts,D[0]),label='Deformation Potential = %.2f eV'%D[0])
legend(loc=0)
ylabel('Mobility [cm^2/(V*s)]')
xlabel('Temperature [K]')
show()

拟合结果中明显可以看到迁移率与温度的反比 (~1/T) 的关系，与（$\ref{7}$）式符合很好。计算得到的形变势 8.8eV 比已报道的结果略小[KTJ12b]。

迁移率 $\mu$ 与电导率 $\sigma$ 有如下关系： $$ \mu = \frac{\sigma}{ne} \tag{1}\label{1}$$

$n$ 表示载流子浓度，$e$ 表示电子电荷。

本文中，我们将采用半经典玻尔兹曼输运方程（BTE）计算电导率。在零磁场和恒定电场下，定态玻尔兹曼方程简化为： $$\frac{q\mathbf{E}}{\hbar} \cdot \nabla_{\mathbf{k}} f_{\mathbf{k} n} \approx \frac{q\mathbf{E}}{\hbar} \cdot \nabla_{\mathbf{k}} f^0_{\mathbf{k} n} = \left.\frac{\partial f_{\mathbf{k}n}}{\partial t}\right|_{coll} \tag{2}\label{2}$$

方程($\ref{2}$)右侧，常被称为碰撞积分（collision integral）,用来描述不同的散射机制。由多种机制散射后，系统可耗散至稳态。方程左侧与电场强度线性相关，比例系数由分布函数决定。

电声子散射由碰撞积分描述，通常采用弛豫时间近似： $$\left.\frac{\partial f_{\mathbf{k}n}}{\partial t}\right|_{coll} = \frac{\delta f_{\mathbf{k}n}}{\tau_{\mathbf{k}n}}$$

描述声学声子的准弹性散射（弛豫时间近似）。用 $\lambda$ 标记声子模式，$n$ 标记电子能带，$k$ 标记电子波矢。由 $|\mathbf{k}n\rangle$ 态到 $|\mathbf{k}'n'\rangle$ 态的跃迁几率可以由 费米黄金规则（FGR）得到：

$$\begin{split}P_{\mathbf{k}\mathbf{k'}}^{\lambda nn'} &= \frac{2\pi}{\hbar} |g_{\mathbf{k}\mathbf{k'}}^{\lambda n n'}|^2 [ n_{\mathbf{q}}^{\lambda} \delta \left(\epsilon_{\mathbf{k}'n'}-\epsilon_{\mathbf{k}n}-\hbar \omega_{q \lambda} \right) \delta_{\mathbf{k}',\mathbf{k}+\mathbf{q}} \\[.5cm] &+ (n_{\mathbf{-q}}^{\lambda}+1) \delta \left( \epsilon_{\mathbf{k}'n'}-\epsilon_{\mathbf{k} n}+\hbar \omega_{-q \lambda} \right) \delta_{\mathbf{k}',\mathbf{k}-\mathbf{q}} ],\end{split}$$

方括号中第一项和第二项分别表示吸收一个声子和放出一个声子。在 QuantumATK 中，使用 ElectronPhononCoupling 分析模块计算电声子耦合矩阵元 $ |g_{\mathbf{k}\mathbf{k'}}^{\lambda n n'}|$。从而得到电声子碰撞积分：

$$\begin{split}\left.\frac{\partial f_{\mathbf{k}n}}{\partial t}\right|_{coll} &= - \sum_{\mathbf{k}'n'} \left[f_{\mathbf{k}n}\left(1-f_{\mathbf{k}'n'}\right)P_{\mathbf{k}\mathbf{k}'}^{nn'}-f_{\mathbf{k}'n'}\left(1-f_{\mathbf{k}n}\right)P_{\mathbf{k}'\mathbf{k}}^{n'n}\right]\end{split} \tag{3}\label{3}$$

弛豫时间近似，是采用非常简单的形式来表示碰撞积分： $$\begin{split}\left.\frac{\partial f_{\mathbf{k}n}}{\partial t}\right|_{coll} &=& -\frac{\delta f_{\mathbf{k}n}}{\tau_{\mathbf{k}n}}\end{split} \tag{4}\label{4}$$

其中 $\delta f_{\mathbf{k}n} = f_{\mathbf{k}n}-f^0_{\mathbf{k}n}$。因此，线性玻尔兹曼输运方程可写为： $$q \mathbf{E} \cdot \mathbf{v}_{\mathbf{k} n} \frac{\partial f^0_{\mathbf{k}n}}{\partial \epsilon_{\mathbf{k}n}} = -\frac{\delta f_{\mathbf{k}n}}{\tau_{\mathbf{k} n}}.$$

于是有： $$\delta f_{\mathbf{k}n} = -q \mathbf{E} \cdot \mathbf{v}_{\mathbf{k} n} \frac{\partial f^0_{\mathbf{k}n}}{\partial \epsilon_{\mathbf{k}n}} \tau_{\mathbf{k} n}.$$

弛豫时间可由（$\ref{3}$）式碰撞积分的一般形式计算得到。在准弹性散射近似下，($\omega_{q \lambda}\rightarrow 0$)，($\ref{4}$）式的特殊形式成立，（$\ref{3}$）式中的碰撞积分可简化为：

$$\left.\frac{\partial f_{\mathbf{k}n}}{\partial t}\right|_{coll}^{RTA} = \sum_{\mathbf{k}'n'} \left(f_{\mathbf{k}'n'}-f_{\mathbf{k}n}\right) P_{\mathbf{k}\mathbf{k'}}^{nn'} \equiv -\frac{\delta f_{\mathbf{k}n}}{\tau_{\mathbf{k} n}}$$,

因为在该近似下，$P_{\mathbf{k}\mathbf{k'}}^{nn'} = P_{\mathbf{k}'\mathbf{k}}^{n'n}$。

由此，我们得到散射几率（弛豫时间倒数）的表达式： $$\frac{1}{\tau_{\mathbf{k} n}} = \sum_{\mathbf{k}'n'} \left(1-\frac{\delta f_{\mathbf{k}'n'}}{\delta f_{\mathbf{k}n}}\right) P_{\mathbf{k}\mathbf{k'}}^{nn'} \tag{5}\label{5}$$

这里，应用了细致平衡方程 $P_{\mathbf{k}\mathbf{k'}}^{nn'}(f^0_{\mathbf{k}'n'}-f^0_{\mathbf{k}n})=0$，并假设散射各向同性。

为计算弛豫时间，我们引入散射角的概念 $$cos(\theta_{\mathbf{k}\mathbf{k'}}) = \frac{\mathbf{v}_{\mathbf{k}'n'} \cdot \mathbf{v}_{\mathbf{k}n}}{|\mathbf{v}_{\mathbf{k}'n'}| |\mathbf{v}_{\mathbf{k}n}|}$$

其中，$\mathbf{v}_{\mathbf{k}n}$ 表示电子速度。由文献【GMSB16】可得： $$\frac{1}{\tau_{\mathbf{k} n}} =\sum_{\mathbf{k}'n'} \frac{(1-f^0_{\mathbf{k}'n'})}{(1-f^0_{\mathbf{k}n})}\left(1-cos(\theta_{\mathbf{k}\mathbf{k'}})\right) P_{\mathbf{k}\mathbf{k'}}^{nn'}$$

由弛豫时间，我们可以计算迁移率： $$\mu = -2q \frac{\sum_{\mathbf{k}n} v_{\mathbf{k} n}^2 \frac{\partial f^0_{\mathbf{k}n}}{\partial \epsilon_{\mathbf{k}n}} \tau_{\mathbf{k} n}}{\sum_{\mathbf{k}n}f^0_{\mathbf{k}n}} \tag{6}\label{6}$$

其中因子 2 表示自旋简并。

由上述公式推导可以看到，迁移率计算是一项大型数值计算任务，这也是采用多个近似的进行简化处理的原因。一个非常常用的近似是形变势近似。电声子耦合矩阵元用解析公式表示，从而直接计算上述公式的积分值。

在形变势近似中，电子-声子耦合项表示为： $$ | \langle \mathbf{k + q}|\delta V_\mathbf{q} | \mathbf{k} \rangle| = |M_{\mathbf{k},\mathbf{q}}| = D^{(1)}\cdot q $$

其中 $D^{(1)}$ 表示一阶形变势。一些声子模式（特别是光学模）零阶形变势已足够准确，即 $|M_{\mathbf{k},\mathbf{q}}|=D^{(0)}$ 与 $q$ 无关。

考虑仅有一个有效声速为$v_{eff}$的声学声子模，产生各向同性一阶形变势$D_{eff}$，迁移率在高温区的解析表达式可写为： $$\mu = \frac{4e\,\hbar\,\rho \,v_F^2 v_{eff}^2}{\pi\, n \, D_{eff}^2 k_B T} \tag{7}\label{7}$$

其中 $\rho$ 表示质量密度，$n$ 为载流子浓度。石墨烯中的 $n$ 与费米能量 $E_F$ 相关，$E_F = \alpha \sqrt{n}$。在高温区，迁移率与温度成反比。在低温极限下，迁移率服从 Bloch-Gruneisen 规律。在 Bloch-Gruneisen 温度 ($T_{BG}=2\hbar\,k_F\,v_s\,/k_B$) 以下，由于反散射 (back-scattering) 的相空间缩减，载流子寿命随温度降低而迅速增加，迁移率比 $T^{-1}$ 更快的增加。【文献KTJ12b】

• [GMSB16] (1, 2, 3) T. Gunst, T. Markussen, K. Stokbro, and M. Brandbyge. First-principles method for electron-phonon coupling and electron mobility: Applications to two-dimensional materials. Phys. Rev. B, 93:035414, Jan 2016. doi:10.1103/PhysRevB.93.035414.
• [HS08] EH Hwang and S Das Sarma. Acoustic phonon scattering limited carrier mobility in two-dimensional extrinsic graphene. Physical Review B, 77(11):115449, 2008.
• [KTJ12] K. Kaasbjerg, K. S. Thygesen, and K. W. Jacobsen. Phonon-limited mobility in n-type single-layer mos2 from first principles. Phys. Rev. B, 85:115317, Mar 2012. doi:10.1103/PhysRevB.85.115317.
• [KTJ12b] (1, 2, 3, 4, 5, 6) Kristen Kaasbjerg, Kristian S Thygesen, and Karsten W Jacobsen. Unraveling the acoustic electron-phonon interaction in graphene. Physical Review B, 85(16):165440, 2012.
• [KS92] T Kawamura and S Das Sarma. Phonon-scattering-limited electron mobilities in al x ga 1- x as/gaas heterojunctions. Physical review B, 45(7):3612, 1992.

(本文翻译：朱元慧)